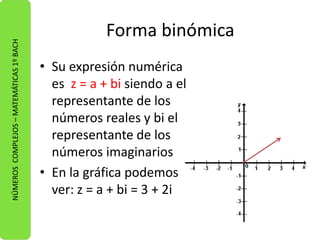
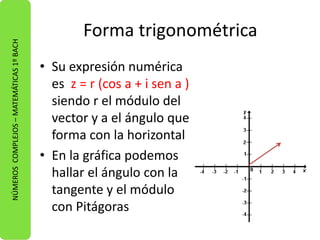
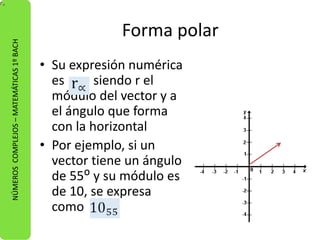
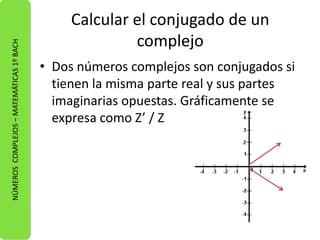
Los números complejos están formados por una parte real y otra imaginaria. Pueden expresarse de tres formas: binómica, trigonométrica y polar. La forma binómica es a + bi, donde a es la parte real e i la imaginaria. La forma trigonométrica es r(cosa + isina), donde r es el módulo y a el ángulo. La forma polar es reia, con r el módulo y a el ángulo. Se explican operaciones como suma, resta, multiplicación, división y potenciación de números complejos.

1. NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH
NÚMEROS COMPLEJOS

2. definición
• Los números complejos son números
formados por una parte real ( a ) y por otra
parte imaginaria ( bi ).
• Se denomina unidad imaginaria ( i ) al
número
• los números complejos se pueden expresar
de 3 maneras: binómica, trigonométrica y
polar.
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

3. Forma binómica
• Su expresión numérica
es z = a + bi siendo a el
representante de los
números reales y bi el
representante de los
números imaginarios
• En la gráfica podemos
ver: z = a + bi = 3 + 2i
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

4. Forma trigonométrica
• Su expresión numérica
es z = r (cos a + i sen a )
siendo r el módulo del
vector y a el ángulo que
forma con la horizontal
• En la gráfica podemos
hallar el ángulo con la
tangente y el módulo
con Pitágoras
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

5. Forma polar
• Su expresión numérica
es siendo r el
módulo del vector y a
el ángulo que forma
con la horizontal
• Por ejemplo, si un
vector tiene un ángulo
de 55ᴼ y su módulo es
de 10, se expresa
como
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

6. Calcular el módulo del vector
• Como la punta del vector forma un ángulo
de 45ᴼ con la horizontal y la distancia tiene
componentes X e Y (catetos 1 y 2), por eso
utilizamos el Teorema de Pitágoras.
• Ejemplo:
X = 3 m
Y = 4 m
r = 5 m
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

7. Calcular el opuesto de un complejo
• El opuesto de un vector es ese mismo
vector multiplicado por -1. gráficamente se
expresa como -Z
• Ejemplo:
Z = 3 + 4i
- Z = - 3 – 4i
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

8. Calcular el conjugado de un
complejo
• Dos números complejos son conjugados si
tienen la misma parte real y sus partes
imaginarias opuestas. Gráficamente se
expresa como Z’ / Z
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

9. Calcular el inverso de un complejo
El inverso de z ≠ 0 es el número Z elevado a -
1, o lo que es lo mismo, 1 / Z
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

10. NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH
Operaciones con complejos en
forma binómica

11. Suma y diferencia
Suma: ( a + bi ) + ( c + di ) = ( a + c ) + ( b + d )i
suma: ( 2 + 3i ) + (4 + 8i ) = 6 + 11i
Diferencia:
( a + bi ) - ( c + di ) = ( a + c ) - ( b + d )i
( 2 + 3i ) - (4 + 8i ) = -2 -5i
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

12. Multiplicación y división
( a + bi ) * ( c + di ) = ac – bd + ( ad + bc) i
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

13. Potencia de números complejos
Cada 4 potencias el resultado se repite, así
que para hallar el resultado se divide entre 4
y el resto ( 1 / 2 / 3 / 4 ) nos indicará cual hay
que establecer
NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH

14. NÚMEROS COMPLEJOS – MATEMÁTICAS 1º BACH
Operaciones en forma polar