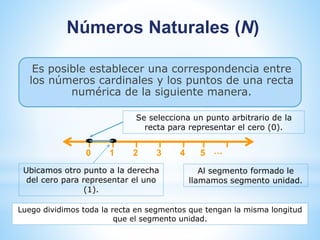
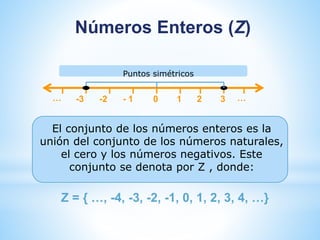
Este documento describe los diferentes conjuntos numéricos, incluyendo números naturales, enteros, racionales, irracionales y reales. Explica que cada conjunto se amplía para incluir nuevos tipos de números a medida que surgen necesidades matemáticas. Define cada conjunto y proporciona ejemplos de los tipos de números que contiene.

1. Números Reales
Estándares: Pensamiento Numérico y Variacional
Logro e indicadores:
Identificar las características, las relaciones y las propiedades
del conjunto de los números reales.
• Identifica las relaciones de contenencia entre los conjuntos
numéricos.
• Reconoce las diferencias entre los números que pertenecen
a uno u otro conjunto numérico.
• Determina la pertenencia de un número a un conjunto
numérico.
• Representa gráficamente números reales.
• Compara números reales.
• Reconoce las propiedades que cumplen las operaciones
dentro de los diferentes sistemas numéricos.
• Realiza operaciones entre distintos conjuntos numéricos.

2. Números Reales
Los conjuntos numéricos se van ampliando a
medida que se necesitas resolver ciertas
problemáticas de la vida diaria.
Estos conjuntos numéricos reciben un
nombre de acuerdo a los números que
contienen.

3. Números Naturales (N)
Los números naturales son un
conjunto de números de la
forma:
IN = {1, 2, 3, 4, 5 ...}
Si al conjunto N se le une el
número cero, este nuevo
conjunto se denota N0, y sus
elementos son llamados
números cardinales.
IN0 = {0, 1, 2, 3...}

4. Números Naturales (N)
Es posible establecer una correspondencia entre
los números cardinales y los puntos de una recta
numérica de la siguiente manera.
Se selecciona un punto arbitrario de la
recta para representar el cero (0).
0 1 2 3 4 5 …
Ubicamos otro punto a la derecha
del cero para representar el uno
(1).
Al segmento formado le
llamamos segmento unidad.
Luego dividimos toda la recta en segmentos que tengan la misma longitud
que el segmento unidad.

5. Números Naturales (N)

6. Números Naturales (N)
De N y N0 se pueden formar
variados subconjuntos, entre ellos se
encuentran:
El Conjunto de los números pares es un subconjunto de N0
donde:
{x Є N0 / x=2n, n Є N0 } = {0, 2, 4, 6, 8, 10,....}
El Conjunto de los números impares es un subconjunto de IN0
donde:
{x Є N0 / x=2n + 1, n Є No } ={1,3,5,7,9,11,...}
Observa que estos dos conjuntos no tienen elementos en
común y que si se unen ambos, forman el conjunto.

7. Números Naturales (IN)
Otros subconjuntos de N son:
El conjunto de los Múltiplos de un número n:
{1n, 2n, 3n,4n, … }.
El conjunto de los Divisores de un número:
Llamamos divisores de un número, a todo el conjunto de números que
lo divide exactamente.
El conjunto de los Números Primos:
El número natural p >1 es un número primo si sus únicos divisores
son 1 y p.

8. Números Enteros (Z)
Puntos simétricos
… -3 -2 - 1 0 1 2 3 …
El conjunto de los números enteros es la
unión del conjunto de los números naturales,
el cero y los números negativos. Este
conjunto se denota por Z , donde:
Z = { …, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}

9. Números Enteros (Z)

10. Números Enteros (Z)
Cada número negativo es considerado el
opuesto o inverso aditivo de su simétrico
positivo y, cada número positivo, es el
opuesto de su simétrico negativo.
El valor absoluto de un número a es la
distancia que existe entre el cero y el
número y se expresará como |a|.
El valor absoluto es siempre positivo.
Inverso aditivo
Valor Absoluto

11. Números Racionales (Q)
El conjunto de los números racionales lo
denotaremos Q, y se define de la siguiente
forma:
Decimos que a es un número racional,
si es posible expresarlo de la forma
donde p, q Є Z y q ≠ 0 .
p
q
a 

12. Números Racionales (Q)

13. Números Irracionales (I)
Un número irracional es un decimal infinito,
cuya parte decimal no posee periodo, es
decir, no puede ser representado como
racional.
Todas las raíces inexactas son números
irracionales.
Algunos irracionales son:
 2 2

… 4
-3 -2 - 1 0 1 2 3 …

14. Números Irracionales (I)

15. Números Reales (R)
El conjunto de los números reales se denota
por la letra R y está conformado por la unión
del conjunto de los números racionales con el
conjunto de los números irracionales:
IR
Q
Z
-7 -5
N
I
-8 1,2,3,...,
20,...
0
0,125
21
4
0,125555555
2 1,414213.. .
  3,14159...

16. Números Reales (R)

17. GRACIAS