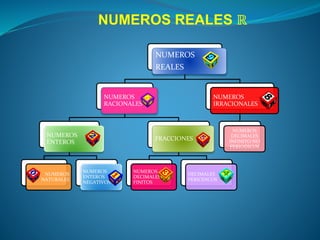
Este documento describe los diferentes tipos de números, incluyendo números naturales, enteros, racionales, irracionales y reales. Explica que los números naturales se usan para contar cantidades, mientras que los números enteros incluyen también los números negativos. Finalmente, introduce las fracciones como una forma de expresar números racionales, y los decimales periódicos y no periódicos como ejemplos de números reales.

1. NUMEROS
REALES
NUMEROS
RACIONALES
NUMEROS
ENTEROS
NUMEROS
NATURALES
NUMEROS
ENTEROS
NEGATIVOS
FRACCIONES
NUMEROS
DECIMALES
FINITOS
DECIMALES
PERIODICOS
NUMEROS
IRRACIONALES
NUMEROS
DECIMALES
INFINITO NO
PERIODICOS
NUMEROS REALES ℝ

2. Los números naturales sirve para designar la cantidad de
elementos que tiene un cierto conjunto, y se llama cardinal de
dicho conjunto. Los números naturales son infinitos. El conjunto de
todos ellos se designa por N:
N = {0, 1, 2, 3, 4,…, 10, 11, 12,…}
El cero, a veces, se excluye del conjunto de los números naturales.
Además de cardinales (para contar), los números naturales son
ordinales, pues sirven para ordenar los elementos de un conjunto:
1º (primero), 2º (segundo),…, 16º (decimosexto),…

3. Número entero NEGATIVOS esta formado por los opuestos de
los números naturales. El conjunto de los números enteros se
designa por ℤ−
:
ℤ−
= {…, -11, -10,…, -2, -1}
Un ejemplo de números enteros negativos se utilizan en la
temperatura cuando se nombra bajo cero. 5 grados bajo cero = -5
grados
por debajo del nivel del mar, 120 metros debajo el nivel del mar =
- 120 metros
Cuando hablamos de deudas… entre otros ejemplos.

4. El conjunto de los Números Enteros esta formado por los enteros
negativos, los enteros positivos(naturales) y el cero. El conjunto de
los números enteros se designa por Z:
ℤ = ℤ+
∪ ℤ−
∪ 0
Z = {…, -11, -10,…, -2, -1, 0, 1, 2,…, 10, 11,…}
Se llama valor absoluto de un número entero a, a un número natural
que se designa |a| y que es igual al propio a si es positivo o cero, y a
-a si es negativo. Es decir:
• si a > 0, |a| = a ; por ejemplo, |5| = 5;
El valor absoluto de un número es, pues, siempre positivo.

5. Las operaciones suma, resta y multiplicación de números enteros son operaciones
internas porque su resultado es también un número entero. Sin embargo, dos
números enteros sólo se pueden dividir si el dividendo es múltiplo del divisor.
Suma de Números Enteros. Para sumar dos números enteros se procede del
siguiente modo:
• Si tienen el mismo signo, se suman sus valores absolutos, y al resultado se le
pone el signo que tenían los sumandos: • 7 + 11 = 18 • -7 - 11 = -18
• Si tienen distintos signos, es decir, si un sumando es positivo y el otro negativo, se
restan sus valores absolutos y se le pone el signo del mayor:
• 7 + (-5) = 7 - 5 = 2 • -7 + 5 = - (7 - 5) = -2 • 14 + (-14) = 0
La suma de números enteros tiene las propiedades siguientes:
Asociativa: (a + b) + c = a + (b + c)
Conmutativa: a + b = b + a
Elemento neutro: el cero es el elemento neutro de la suma, a + 0 = a
Elemento opuesto: todo número entero a, tiene un opuesto –a, a + (-a) = 0
OPERACIONES CON NUMEROS ENTEROS

6. OPERACIONES CON NUMEROS ENTEROS
Multiplicación de Números Enteros
Para multiplicar dos números enteros se multiplican sus valores absolutos y el
resultado se deja con signo positivo si ambos factores son del mismo signo o se
le pone el signo menos si los factores son de signos distintos. Este
procedimiento para obtener el signo de un producto a partir del signo de los
factores se denomina regla de los signos y se sintetiza del siguiente modo:
+ · + = + + · - = - - · + = - - · - = +
La multiplicación de números enteros tiene las propiedades siguientes:
Asociativa: (a · b) · c = a · (b · c)
Conmutativa: a · b = b · a
Anulativa o absorbente: a.0 =0.a =0
Elemento neutro: el 1 es el elemento neutro de la multiplicación, a · 1 = a
Distributiva de la multiplicación respecto de la suma: a · (b + c) = a · b + a · c
Resta de Números Enteros
Para restar dos números enteros se le suma al minuendo el opuesto del
sustraendo: a - b = a + (-b) .
Por ejemplo: | 5 - (-3) = 5 + 3 = 8
-2 - 5 = (-2) + (-5) = -7

7. Una fracción es una expresión de la forma
𝑎
𝑏
, en la que a y b son
números enteros, con b≠0. En dicha expresión llamaremos: a →
numerador y
b → denominador
La fracción como cociente La fracción
𝑎
𝑏
, expresa el cociente de dos
números enteros a y b (a:b). Calculamos su valor dividiendo el
numerador entre el denominador.
Ejemplo: Tenemos 28 gomitas iguales para repartir entre 4 niños. El
número de gomitas que le corresponde a cada niño es
28
4
→ 28 : 4 =7
gomitas le tocan a cada niño.
Las fracciones que tienen el numerador igual que el denominador son iguales a
la unidad, y recíprocamente, el 1 se puede expresar como una fracción en la que
coinciden numerador y denominador.
Ejemplo:
8
8
=1 ; :
81
81
=1 ; :
13
13
=1

8. Ejemplo: Fracción decimal
𝟏𝟐
𝟏𝟎𝟎
= 𝟎, 𝟏𝟐 Número decimal
FRACCIONES ORDINARIAS
son las que tienen por denominador un número que no es la unidad seguida
de ceros; para escribir una fracción ordinaria en forma de número decimal
basta con dividir el numerador por el denominador, y el cociente obtenido es
un número decimal.
Fracción ordinaria
𝟔
𝟒
= 𝟏, 𝟓 Número decimal
Un decimal es FINITO O EXACTO cuando al realizar las cifras son finitas, es
decir que en algún momento aparece cero en el residuo.
DECIMALES FINITOS
FRACCIONES DECIMALES
son las que tienen por denominador una potencia de 10, es decir, la unidad
seguida de ceros.

9. DECIMALES PERIODICOS
Cuando al realizar la división las cifras decimales son infinitas y
se repiten inmediatamente después de la coma, se llaman
decimales periódicos puros.
La raya sobre el numero indica que éste es el que se repite
infinitamente.
Ejemplo:
7
9
; se realiza la división 7/9=0,77777…. =0,7
Decimales periódico mixta: cuando al realizar la división las
cifras decimales que se repiten no aparecen inmediatamente
después de la coma.
Ejemplo:
13
6
; se realiza la división
13/6=2,166666.... =2,16

10. Los números racionales son aquellos que pueden representarse como
el cociente de dos enteros con denominador distinto de cero, o sea,
como una fracción común. Se representa por ℚ.
.
Ejemplo: ℚ = … . . , −5,
−4,
3
, −2, −1,0, 1, 2, 3,
16
4
, 5, … …

11. Con números racionales se realizan las operaciones: adición,
sustracción, multiplicación y división,
ADICION Y SUSTRACCION
• Suma y resta de números racionales con el mismo denominador
Se suman o se restan los numeradores y se mantiene el
denominador.
Ejemplos:
•

12. • Suma y resta de números racionales con distinto
denominador
En primer lugar se reducen los denominadores a común
denominador, y se suman o se restan los numeradores de las
fracciones equivalentes obtenidas.
Ejemplos:
PROPIEDADES DE LA ADICION DE NUMEROS
RACIONALES.
Propiedad clausurativa o interna
El resultado de sumar dos números racionales es otro número
racional.

13. Propiedad asociativa. El modo de agrupar los sumandos no
varía el resultado.
(a + b) + c = a + (b + c)
Ejemplo: