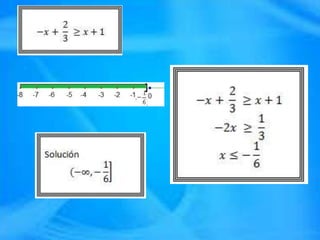
Este documento trata sobre las inecuaciones. Explica que una inecuación es una desigualdad algebraica donde se desconoce el valor de al menos una variable. La solución de una inecuación puede expresarse de dos formas: una representación gráfica o un intervalo. También clasifica los diferentes tipos de intervalos y explica los pasos para resolver inecuaciones, incluyendo el uso de la propiedad distributiva, agrupar términos semejantes, graficar y hallar el intervalo solución.

1. Inecuaciones
NORLAN MIRANDA
del concepto
Prof. Dechima Sabrina

2. Sabrina Dechima
¿Qué es una inecuación?
Las inecuaciones son desigualdades algebraicas
en la que hay al menos una variable cuyo valor
se desconoce, y sus miembros se relacionan por
algunos de estos signos
La solución de una inecuación, es el conjunto de
valores de la variable que la verifica, hay dos
formas de expresarla
 Una representación grafica

3. Sabrina Dechima
Un intervalo

4. Sabrina Dechima
Clasificación de Intervalos
Intervalo Abierto: “Los extremos no
pertenecen al Intervalo”.Ej:
Intervalo Cerrado: “Ambos extremos
pertenecen al intervalos”.Ej:

5. Sabrina Dechima
Intervalo Finito: “Son los que tiene principioy
fin”.Ej:
Intervalo Infinito: “Son los que tienen
principio y no fin o viceversa” Ej

6. Sabrina Dechima

7. Para comenzar
Primero propiedad
distributiva
Se agrupan los términos
semejantes
Se grafica
Se halla el intervalo
solución
Sabrina Dechima

8. Sabrina Dechima
Cuando en una
inecuación se pasa
multiplicando o
dividiendo por un
número negativo,
se debe invertir el
signo de la
desigualdad
Sabrina Dechima

10. Sabrina Dechima
Inecuaciones con
doble planteo
Sabrina Dechima

11. Veamos un ejemplo
Empecemos a analizar:
 El denominadorNUNCA puede ser cero
 Además tenemos un cociente que es menor a
cero, es decir siempre será negativo. Por eso
es necesario recurrir a la regla de signos.

12. Sabrina Dechima
Será necesario plantear dos posibilidades

13. Resolvemos cada una de las Inecuaciones
Sabrina Dechima

14. Sabrina Dechima
Pero . . . ¿Cuál es el conjunto
solución?
Ya tenemos la solución de las intersecciones,
ahora falta unir estos resultados.
En este caso es una unión porque viene de un
“o”, de modo que son validas cualquierade
las dos ramas en las que dividimos el planteo,
por lo tanto debemos unir los resultados
obtenidos en cada una

15. La solución final

16. Sabrina Dechima
Veamos otro ejemplo
Lo primero que
tenemos que hacer
es llevarlo a la
“estructura” que
posee el ejercicio
anterior

17. Sabrina Dechima
Empecemos a analizar:
 El denominadorNUNCA puede ser cero
 Además tenemos un cociente que es mayor a
cero, es decir siempre será positivo. Por eso es
necesario recurrir a la regla de signos.
Será necesario plantear dos posibilidades

18. Sabrina Dechima

19. Sabrina Dechima
La solución final es
Veamos un nuevo ejemplo pero ahora
incluiremos la igualdad en la ecuación
En este caso el cociente es positivo o cero

20. Sabrina Dechima
Planteamos primero la posibilidad
de que sea cero.
Para que la expresión sea cero, debe ser cero el
numerador y el denominadordebe ser siempre
distinto de cero

21. Sabrina Dechima
Esto significa que x = -3 es parte de la solución
de esta inecuación,ya que con este valor la
expresión se hace cero

22. Ahora planteamos la parte del , para ello
plantearemos las dos desigualdades
Sabrina Dechima

23. Ahora analicemos cual será el conjunto solución
La solución final será la UNION DE TODO
(incluyendo x=-3)
Observen que al incluir x = -3 ponemos
corchetes en el intervalo de manera que este
lo contenga
Sabrina Dechima

24. sabrinamatematica@blosgspot.com.ar
Si deseas dejar un comentario o ver nuevamente
la presentación puedes hacer lo en
Sabrina Dechima