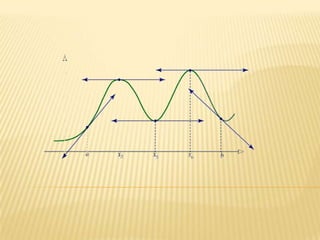
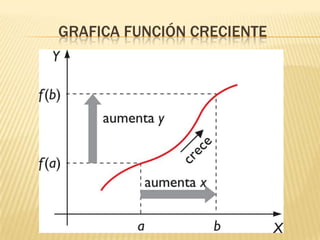
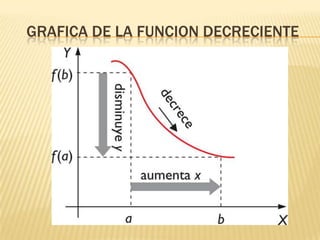
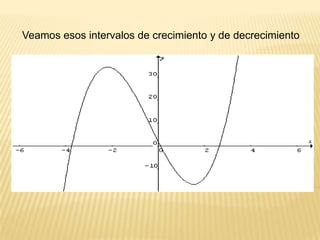
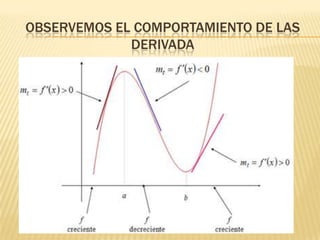
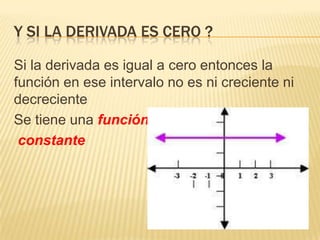
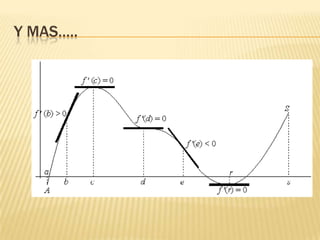
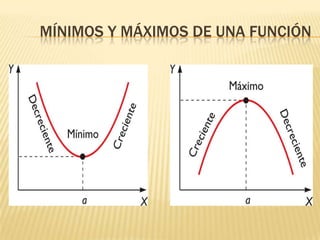
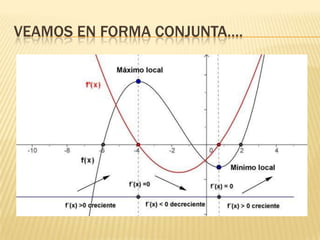
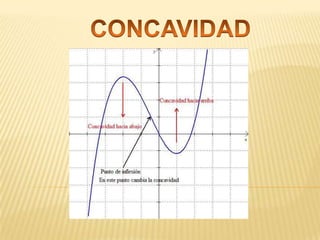
Este documento describe la variación de funciones y cómo determinar si una función es creciente, decreciente o constante mediante el análisis de la derivada. Explica que una función es creciente cuando la derivada es positiva e indica que los valores de f(x) aumentan a medida que aumentan los valores de x. Una función es decreciente cuando la derivada es negativa e implica que los valores de f(x) disminuyen cuando aumentan los valores de x. Si la derivada es cero, la función es constante. Además, analiza los mínimos,

1. OPTIMIZACIÓNCLÁSICA

2. VARIACIÓN DE FUNCIONESSi observamos una gráfica vemos que en unos puntos la gráfica sube (Crecimiento), otros en los que baja (Decrecimiento) y otros en los que ni sube ni baja, es decir, permanece constante. Estos aumentos o disminuciones de la variable dependiente es lo que denominamos variación de la función.

4. Intervalos en que la función es crecienteEn el intervalo en que la función es creciente los valores de f(x) aumentan a medida que aumentan los valores de xLa derivada es siempre positiva en el intervalo en que la función es creciente

5. Grafica función creciente

6. Intervalos en que la función es decrecienteEn el intervalo en que la función es decreciente los valores de f(x) disminuyen a medida que aumentan los valores de x, o viceversaLa derivada es siempre negativa en el intervalo en que la función es decreciente

7. Grafica de la funcion decreciente

8. Veamos esos intervalos de crecimiento y de decrecimiento

9. RECUERDE QUE:La derivada de una función es positiva en el intervalo donde la función es creciente “Derivada (+) entonces es CRECIENTE”La derivada de una función es negativa en el intervalo donde la función es decreciente “Derivada (--) entonces es DECRECIENTE”

10. OBSERVEMOS EL COMPORTAMIENTO DE LAS DERIVADA

11. Y si la derivada es cero ?Si la derivada es igual a cero entonces la función en ese intervalo no es ni creciente ni decrecienteSe tiene una función constante

12. Y MAS…..

13. Mínimos y máximos de una función

14. Veamos en forma conjunta….

15. CONCAVIDAD

16. Final de la presentaciónPOR: LIC JORGE SANTANDER