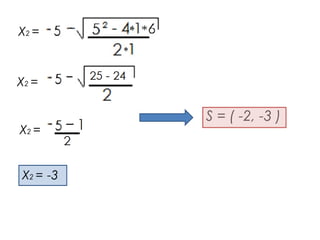
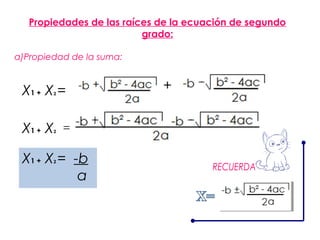
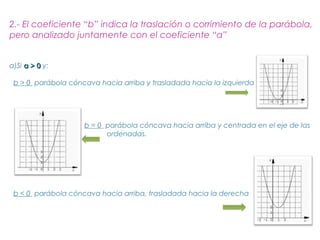
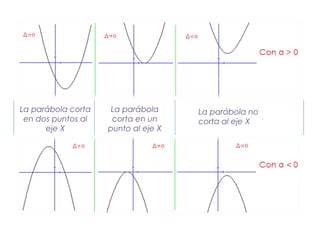
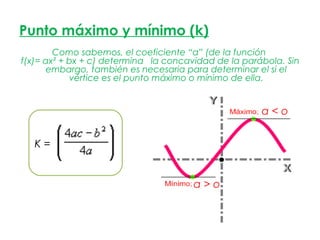
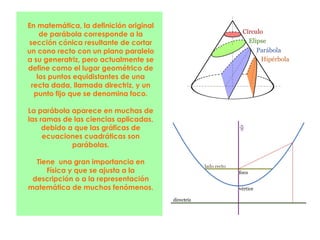
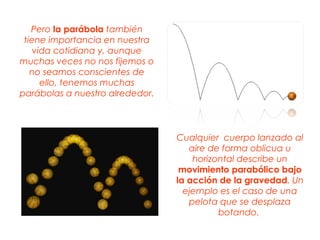
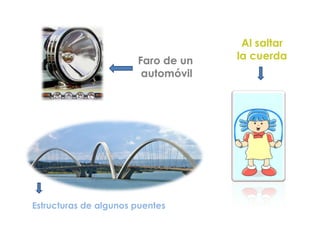
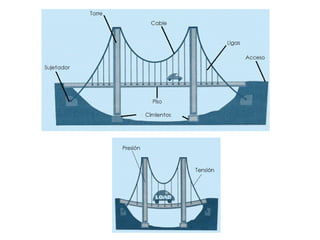
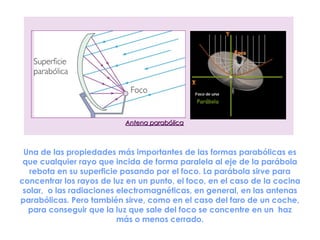
La parábola se define como el lugar geométrico de los puntos equidistantes de una recta fija llamada directriz y un punto fijo llamado foco. Tiene importancia en física y la vida cotidiana, ya que describe fenómenos como el movimiento de objetos lanzados y la forma de antenas, faros y puentes. Las parábolas permiten converger o diverger haces de luz y sonido. Tienen propiedades como reflejar rayos de luz incidentes paralelos al eje hacia el foco.

1. Parábolas y
Ecuación de segundo
grado  Viviana Soto
 Daniela Valenzuela
 Daniela Reyes
III ½ B 2010

2. En matemática, la definición original
de parábola corresponde a la
sección cónica resultante de cortar
un cono recto con un plano paralelo
a su generatriz, pero actualmente se
define como el lugar geométrico de
los puntos equidistantes de una
recta dada, llamada directriz, y un
punto fijo que se denomina foco.
La parábola aparece en muchas de
las ramas de las ciencias aplicadas,
debido a que las gráficas de
ecuaciones cuadráticas son
parábolas.
Tiene una gran importancia en
Física y que se ajusta a la
descripción o a la representación
matemática de muchos fenómenos.

4. Pero la parábola también
tiene importancia en nuestra
vida cotidiana y, aunque
muchas veces no nos fijemos o
no seamos conscientes de
ello, tenemos muchas
parábolas a nuestro alrededor.
Cualquier cuerpo lanzado al
aire de forma oblicua u
horizontal describe un
movimiento parabólico bajo
la acción de la gravedad. Un
ejemplo es el caso de una
pelota que se desplaza
botando.

5. Las aplicaciones de las parábolas son
básicamente aquellos fenómenos en donde
nos interesa hacer converger o diverger un
haz de luz y sonido principalmente.
Por ejemplo las antenas parabólicas, las
lámparas sordas, los faros de los autos. Se
pueden construir, por la misma propiedad de
las parábolas, hornos solares. Los micrófonos
de ambiente en algunos deportes también
tienen forma paraboloide.
Las parábolas tienen una propiedad. Si se
coloca una bombilla encendida en el foco de
la parábola, algunos haces de luz serán
reflejados por la parábola y todos estos rayos
serán perpendiculares a la directriz. Esta
propiedad es usada en las lámparas sordas o
en los faros de los automóviles estos están
formados por un paraboloide (parábola en 3
dimensiones) de espejos y una bombilla en el
foco de este paraboloide.

6. En algunas lámparas se puede mover la bombilla del foco y
los haces de luz divergirán o convergerán. Este principio
funciona también en las antenas parabólicas. Un satélite
envía información a la Tierra, estos rayos serán
perpendiculares a la directriz por la distancia a la que se
encuentra el satélite. Al reflejarse en el plato de la antena
(blanca, casi siempre) los rayos convergen en el foco en
donde se encuentra un receptor que decodifica la
información. También en los telescopios se usa esta
propiedad.

7. Otro ejemplo es el caso de los
chorros y las gotas de agua que
salen de los caños de las
numerosas fuentes que
podemos encontrar en las
ciudades. El desplazamiento
bajo la acción de la atracción
gravitatoria de la Tierra permite
obtener bonitos arcos
parabólicos.
También se aprecia el
mismo caso en piletas
ubicadas en edificios,
hoteles, etc.

8. Arcos parabólicos en dos de las fuentes que
pueden encontrarse en el Paseo del Prado de
Madrid.

9. También obtenemos formas parabólicas cuando un haz
luminoso de forma cónica se proyecta sobre una pared. Las
líneas parabólicas de la imagen se han obtenido
proyectando un haz de luz sobre una pared blanca.

10. Las parábolas también están
presentes en la arquitectura.

11. Al saltar
Faro de un la cuerda
automóvil
Estructuras de algunos puentes

12. En una montaña rusa
Al jugar fútbol

13. Y en diferentes
Deportes…

15. También en otros casos una parábola es la curva que
adopta un cable que tenga que soportar una carga, un
peso, uniformemente distribuido.
Como por ejemplo: El Golden Gate. (Puente de San
Francisco)

19. Diferentes tipos de
antenas
Antena Parabólica de Televisión

20. Antena parabólica
Una de las propiedades más importantes de las formas parabólicas es
que cualquier rayo que incida de forma paralela al eje de la parábola
rebota en su superficie pasando por el foco. La parábola sirve para
concentrar los rayos de luz en un punto, el foco, en el caso de la cocina
solar, o las radiaciones electromagnéticas, en general, en las antenas
parabólicas. Pero también sirve, como en el caso del faro de un coche,
para conseguir que la luz que sale del foco se concentre en un haz
más o menos cerrado.

21. Guía de Trabajo: “Función Cuadrática”
Objetivos:
Conocer la función cuadrática en sus diversas formas
Graficar la función cuadrática en sus diversas formas
Identificar en un gráfico puntos de intersección con los
ejes de coordenadas, vértice y eje de simetría

22. La Parábola en Matemática se define como:
f(x) = a. x2 + b. x + c

23. 1

24. Para determinar las raíces o ceros de la ecuación de segundo grado,
se pueden emplear por lo menos tres métodos.
1.Método de factorización
2.Completación de cuadrados
3.Fórmula de ecuación de segundo grado.
A continuación se presentarán los siguientes ejemplos:
1. Método de factorización:
X² + 5x + 6 = 0
(x+3) (x+2) = 0, donde tenemos que:
X : (x+3) = 0, para que al multiplicarlo por (x + 2) el producto
1
sea 0 x1= -3
X : (x+2) = 0, para que al multiplicarlo por (x + 3) el producto
2
sea 0 x2= -2

25. 2. Completación de cuadrados
[ (a ± b)² = a² ± 2ab + b² ]
Se debe aislar el término independiente(C) de la
ecuación de segundo grado, la cual debe ser
completa particular, quedando una igualdad con
una parte binomial y la otra parte numérica. Si
tenemos una ecuación completa general, habrá
que transformarla a completa particular.
Por lo tanto, para completar el cuadrado de
binomio siempre debemos sumar y restar: (b ÷ 2)²

26. Ejemplo: x² + 6x + 5 = 0
(b ÷ 2)² = (6/2)²
a=1
b=6
= 3²
c= 5 (término independiente) =9
x² + 6x + 5 = 0
x² + 6x = -5 (aislación del término independiente)
x² + 6x = -5 / +9
x² + 6x + 9 = -5 + 9
(x+3)² = 4 / √
X+3 = ± 2
X1: +2 - 3 = -1
X2: -2 - 3 = -5
S= {-5,-1}

27. 3- Fórmula de ecuación de segundo grado
Siendo la primera
X= solución X1 y la
segunda X2
X1 =
X2 =

28. Ejemplo: x² + 5x + 6 = 0 a=1
b=5
x² + 5x + 6 = 0 c=6
X1 =
X1 =
X1 =
X1 = -2

29. X2 =
X2 =
S = ( -2, -3 )
X2 =
X2 = -3

30. Aactividad n°2:
1.- Una de las raíces de la ecuación 3x² - 4x + 1 = 0 es:
a)-1
b)-1/3
c)4/3
d)1/3
e)3
*Respuesta: d
2.- ¿Cuáles son las soluciones de la ecuación x² + 5x – 6 = 0?
a)3 y 2
b)3 y -2
c)-2 y 3
d)-1 y -6
e)-6 y 1
*Respuesta: e

31. 3.- ¿En cuál de las siguientes ecuaciones ambas soluciones son
mayores que cero y menores que uno?
a) 3x² - 7x + 3 = 0
b) 3x² + 7x + 3 = 0
c) 8x² - 6x – 1 = 0
d) 8x² + 6x + 1 = 0
e) 8x² - 6x + 1 = 0
*Alternativa: e
4.- ¿Cuál es el cuadrado de la mayor de las soluciones de la
ecuación x² - 2x - √5 x + 2 √5 = 0?
a)5
b)4
c)√5
d)-4
e)-5
*Alternativa: a

32. Propiedades de las raíces de la ecuación de segundo
grado:
a)Propiedad de la suma:
X1 + X = 2
+
X1 + X 2
X1 + X = -b
2
a

33. b) Propiedad del producto de raíces
X1 * X =
*
2
X1 * X = 2
X1 * X =
2
X1 * X = c2
En general tenemos:
a x² + (X1 + X2)x + (X1 * X2) = 0

34. Actividad n°3:
1.- ¿Cuál es la suma de las soluciones de la ecuación 5x² + 10x + 1 =
0?
a)-1/5
b)1/5
c)-2
d)2
e)½
*Respuesta: d 
2.- Una ecuación de segundo grado cuyas raíces o ceros, satisfacen
las igualdades (X1 + X2) = -2 y (X1*X2) = 5 es:
a)x² - 2x – 5 = 0
b)x² -2x + 5 = 0
c)x² + 2x + 5 = 0
d)x² + 2x – 5 = 0
e)x² - 5x – 2 = 0
*Respuesta: c

35. 3.- ¿Qué valor debe tener K en la ecuación 3x² - 5kx – 2 = 0, para que
una de sus raíces sea -2?
a)0
b)1
c)-1
d)-20
e)-4
*Respuesta: c 
2.- Una ecuación de segundo grado cuyas raíces son 2 + √5 y 2 - √5 es:
a) x² - 4x -1 = 0
b) x² - 4x + 1 = 0
c) x² - 5x + 1 = 0
d) x² - 5x -1 = 0
e) Ninguna de las anteriores
*Respuesta: a 

36. Gráfica de la función de segundo grado: LA PARÁBOLA
La función de segundo grado permite graficar una parábola.
Se representa como: f(x) = ax² + bx + c
Si analizamos sus coeficientes podemos bosquejar una gráfica.
Es muy importante encontrar las raíces de la ecuación,
analizando primeramente el discriminante para saber el tipo
de raíces, y finalmente, debemos determinar el vértice de la
parábola.
Análisis de la función:
1.- El coeficiente
“a” indica la
concavidad de
la parábola:

37. 2.- El coeficiente “b” indica la traslación o corrimiento de la parábola,
pero analizado juntamente con el coeficiente “a”
a)Si a > 0 y:
b > 0 parábola cóncava hacia arriba y trasladada hacia la izquierda
b = 0 parábola cóncava hacia arriba y centrada en el eje de las
ordenadas.
b < 0 parábola cóncava hacia arriba, trasladada hacia la derecha

38. b) Si a < 0 y:
b > 0 parábola cóncava hacia abajo y trasladada
hacia la derecha
b = 0 parábola cóncava hacia abajo y centrada
en el eje de las ordenadas.
b < 0  parábola cóncava hacia abajo y trasladada
hacia la izquierda

39. 3- El coeficiente “c” indica el lugar en que la parábola se
intersecta con el eje de las ordenadas (y)

40. Actividad n°4
1.Con respecto a la función f(x) = 3x² + 13x – 10 = 0,
¿cuál(es) de las siguientes afirmaciones es (son)
verdadera(s)?
I) Su concavidad está orientada hacia arriba.
II) El punto de intersección con el eje y es (o , -10)
III) f(-5) = 0
a)Sólo I
b)Sólo I y II
c)Sólo I y III
d)Sólo II y III
e)Todas ellas
*Respuesta: e

41. DISCRIMINANTE (▲):
Es la cantidad subrradical que corresponde a las raíces o ceros de la
ecuación de segundo grado. El análisis del discriminante nos permite
clasificar las raíces de la ecuación.
El discriminante se determina por D = b² - 4ac
 Si ▲ es mayor a cero, la parábola corta en dos puntos al eje
X. Las raíces son reales y distintas.
 Si ▲ es igual a cero, la parábola corta en un punto al eje X.
Las raíces son reales e iguales.
 Si ▲ es menor a cero, la parábola no corta al eje X. Las raíces
no son reales, son complejas conjugadas o imaginarias puras.

42. La parábola corta La parábola La parábola no
en dos puntos al corta en un corta al eje X
eje X punto al eje X

43. Actividad n°5
1. ¿ En cuál de las siguientes ecuaciones, las raíces son reales y
distintas?
a) x² - x + 12 = 0
b) x² +3x + 5 =0
c) x² - 4x +3 =0
d) x² +5x + 7 =0
e) x² - 2x + 8 = 0
*Respuesta : c
2. Si el discriminante de la ecuación cuadrática 3x² - 4x + k = 0 es
igual a 4, entonces k =
a) -5/3
b) -1
c) 0
d) 1
e) 5/3
*Respuesta : d

44. 3. Si las raíces de la ecuación x² - 6x + t = 0 son reales e iguales,
entonces t=
a) 9
b) 3
c) 0
d) -3
e) -9
*Respuesta: a
4. Las soluciones de la ecuación de segundo grado x²+bx+c= 0 serán
siempre reales si:
a) b>0yc<0
b) b>0yc>0
c) B<0yc>0
d) B=0yc>0
e) Ninguna de las anteriores
*Respuesta: a

45. Cálculo del vértice de una parábola
Se llama vértice de la
parábola al punto
donde ésta corta a su
( h, k) eje.

46. Eje de simetría (h)
• El eje de simetría es aquella recta paralela al eje Y
(ordenadas) , y que pasa por el vértice de la
parábola.

47. Punto máximo y mínimo (k)
Como sabemos, el coeficiente “a” (de la función
f(x)= ax² + bx + c) determina la concavidad de la parábola. Sin
embargo, también es necesaria para determinar el si el
vértice es el punto máximo o mínimo de ella.
a<o
K=
a>o

48. Actividad n°6:
1. Dada la función f(x) = x² + 2x – 3, ¿cuál(es) de las siguientes aseveraciones
es(son) verdadera(s)?
I) x = 1 es un cero de la función
II) La ecuación del eje de simetría es x = -1
III) El vértice de la parábola es (-1, -4)
a) Sólo I
b) Sólo II
c) Sólo I y II
d) Sólo I y III
e) Todas ellas
*Respuesta: e
2. De la función f(x) = x² - 8x + 15 ¿Cuáles son las coordenadas del vértice?
a) (1, -4)
b) (3, -5)
c) (4, -1)
d) (15, -4)
e) (15, -8)
*Respuesta: c

49. 3. Respecto a la parábola f(x) = x² - 9x + 14, ¿cuál(es) de las siguientes proposiciones
es(son) verdadera(s)?
I) Sus ceros son X1 = 7 y X2 = 2
II) Intersecta al eje y en (0, 14)
III) Su eje de simetría es x = 4
a) Sólo I
b) Sólo II
c) Sólo I y II
d) Sólo I y III
e) I, II y III
*Respuesta: c
4. Dada la parábola f(x) = x² + bx + c . Se pueden determinar las coordenadas del
vértice si se sabe que:
I) Intersecta al eje x en X1 = 2 y X2 = 3
II) b = -5 y c = 1 – b
a) (1) por sí sola
b) (2) por sí sola
c) Ambas Juntas, (1) y (2)
d) Cada una por sí sola, (1) ó (2)
e) Se requiere información
*Respuesta: b 

50. Conclusión
Luego de haber aprendido teóricamente lo que era una parábola jamás
imaginaríamos la importancia de éstas. Aprendimos que vivimos día a día
con ellas, muchas veces sin darnos cuenta. Sin ellas tal vez no podríamos ver
tv, no conseguiríamos esa descarga de adrenalina en una montaña rusa y
no existirán tantos avances en la ciencia. Es sorprendente como una simple
ecuación ; unos simples números escritos pueden llegar a ser parte de algo
cada vez más grande. Desde ser unas simples curvas y líneas en un plano
hasta llegar a ser enormes obras de ingeniería y arquitectura.
Aprendimos con este trabajo a mirar más detenidamente lo que nos rodea.
Las parábolas poseen un gran contenido estético y son muy llamativas por
ser simétricas.
También nos dimos cuenta que no sólo existen figuras concretas con formas
de parábolas, sino que existen diferentes movimientos que forman
parábolas, como por ejemplo: la técnica de lanzamiento de dedos en
voleibol para dar pases, las canastas utilizadas en básquetbol para encestar,
movimientos con cintas y cuerdas en gimnasia rítmica, etc.
Lo que aprendemos no lo aprendemos porque si; todo esto tendrá una
finalidad si lo queremos, podremos hacer grandes cosas con el
conocimiento adquirido y una disposición a hacer algo mejor.

51. Por su atención, muchas
gracias