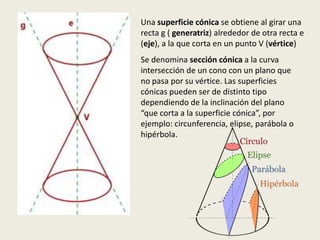
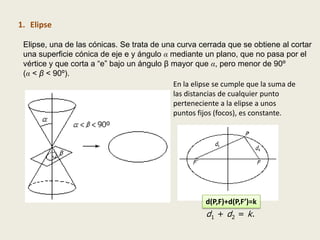
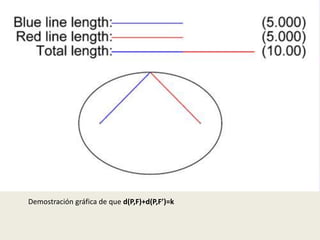
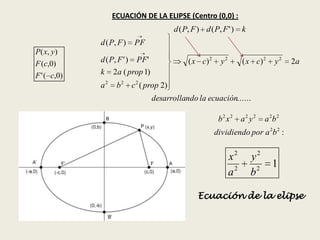
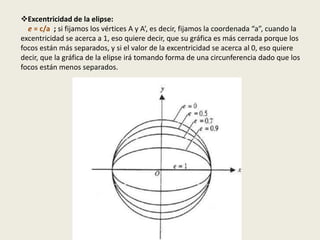
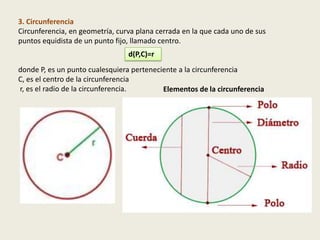
El documento describe las cuatro cónicas principales: la elipse, la hipérbola, la circunferencia y la parábola. Explica cómo se obtienen cada una al cortar una superficie cónica con un plano y define sus elementos característicos. También presenta las ecuaciones geométricas de cada curva cónica y desarrolla las propiedades que permiten derivar dichas ecuaciones.

1. Lugares geométricos. Cónicas
Actividad realizada por ADIL ZIANI
(Matemáticas I, 1º Bach CCNN-Tecnol)

2. Una superficie cónica se obtiene al girar una
recta g ( generatriz) alrededor de otra recta e
(eje), a la que corta en un punto V (vértice)
Se denomina sección cónica a la curva
intersección de un cono con un plano que
no pasa por su vértice. Las superficies
cónicas pueden ser de distinto tipo
dependiendo de la inclinación del plano
“que corta a la superficie cónica”, por
ejemplo: circunferencia, elipse, parábola o
hipérbola.

3. 1. Elipse
Elipse, una de las cónicas. Se trata de una curva cerrada que se obtiene al cortar
una superficie cónica de eje e y ángulo α mediante un plano, que no pasa por el
vértice y que corta a “e” bajo un ángulo β mayor que α, pero menor de 90º
(α < β < 90º).
En la elipse se cumple que la suma de
las distancias de cualquier punto
perteneciente a la elipse a unos
puntos fijos (focos), es constante.
d(P,F)+d(P,F’)=k
d1 + d2 = k.

4. Demostración gráfica de que d(P,F)+d(P,F’)=k

5. Además de los focos F y F´, en una elipse destacan los siguientes elementos:
• Eje focal: recta que contiene a los focos
• A,A’,B y B’ son los vértices de la elipse
• El segmento AA’ es el eje mayor
• El segmento BB’ es el eje menor
• El punto O es el centro.
.d(F,F’)=2c
.d(A,A’)=2a
.d(B,B’)=2b
Propiedades de la elipse:
Prop 1: Si cogemos el vértice A como un punto perteneciente a la elipse, entones se
cumple que: d(A,F)+d(A,F’)=k  d(A,F)+d(A,F’)= d(A,A’)=2a
Entonces obtenemos que
k=2a
Prop 2: También podemos hacer lo mismo con el vértice B, entonces:
d(B,F)+d(B,F’)=k  d(B,F)+d(B,F’)=2a
Como d(B,F)=d(B,F’); obtenemos que: d(B,F)=a , d(B,F’)=a
Así obtenemos una propiedad fundamental de la elipse y es:
 a2 = b2 + c2

6. ECUACIÓN DE LA ELIPSE (Centro (0,0) :
d ( P, F ) d ( P, F ' ) k
d ( P, F ) PF
P ( x, y )
F (c,0) d ( P, F ' ) PF ' ( x c) 2 y2 ( x c) 2 y2 2a
F ' ( c,0) k 2a ( prop 1)
a2 b 2 c 2 ( prop 2)
desarrollando la ecuación......
b2 x2 a2 y2 a 2b 2
dividiendo por a 2b 2 :
x2 y2
1
a2 b2
Ecuación de la elipse

7. Desarrollo de la ecuación

8. Excentricidad de la elipse:
e = c/a ; si fijamos los vértices A y A’, es decir, fijamos la coordenada “a”, cuando la
excentricidad se acerca a 1, eso quiere decir, que su gráfica es más cerrada porque los
focos están más separados, y si el valor de la excentricidad se acerca al 0, eso quiere
decir, que la gráfica de la elipse irá tomando forma de una circunferencia dado que los
focos están menos separados.

9. 2. Hipérbola
Se trata de una curva abierta, formada por dos ramas, que se obtiene al
cortar una superficie cónica de eje e y ángulo α mediante un plano que
no pasa por el vértice y que corta a e con un ángulo β menor que α.
La hipérbola se define como un lugar geométrico de
los puntos del plano cuya diferencia de distancias a
dos puntos fijos llamados focos es constante.
|d(P,F)-d(P,F’)|=k
Elementos de la hipérbola:
Vértices: A y A’ A(a,0); A’(-a,0)
Covértices: B y B’ B(0,b); B’(0,-b)
Eje transversal: recta que contiene los focos
Eje conjugado: recta que contiene a los
covértices
Centro: intersección de los ejes transversal y
conjugado
Asíntotas: recta a las que la curva se acerca
cada vez más en los extremos sin tener
intersección.

10. Propiedades de la hipérbola:
Si cogemos el vértice A como un punto perteneciente a la hipérbola, entonces se
cumple que: |d(A,F)-d(A,F’)|=k
d(A,F’)-d(A,F)=k  d(A,F’)-d(A,F)=d(A,A’)
d(A,F’)-d(A,F)=2a, Entonces llegamos a la
conclusión de que k=2a
Otra propiedad de la hipérbola es la
siguiente: si trazamos una circunferencia
de centro “a” y radio “c”, obtenemos los
covértices B y B’, y obtenemos que:
b2 = c2 – a2

11. ECUACIÓN DE LA HIPÉRBOLA (Centro(0,0)):
d ( P, F ) d ( P, F ' ) k
P ( x, y )
d ( P, F ) PF
F (c,0)
F ' ( c,0) d ( P, F ' ) PF ' ( x c) 2 y2 ( x c) 2 y2 2a
k 2a ( prop 1)
b2 a 2 c 2 ( prop 2)
desarrollando la ecuación......
b2 x2 a 2 y 2 a 2b 2
dividiendo por a 2b 2 :
x2 y2
1
a2 b2
Ecuación de la hipérbola

12. Desarrollo de la ecuación

13. Excentricidad de la hipérbola:
e = c/a ; en la excentricidad de una hipérbola, “c” es siempre mayor que “a” y por tanto
e > 1.
Cuando el valor de “e” se acerca al 1 eso quiere decir que su gráfica es muy cerrada y
cuando el valor de “e” se aleja del 1, su gráfica se hace más abierta

14. 3. Circunferencia
Circunferencia, en geometría, curva plana cerrada en la que cada uno de sus
puntos equidista de un punto fijo, llamado centro.
d(P,C)=r
donde P, es un punto cualesquiera perteneciente a la circunferencia
C, es el centro de la circunferencia
r, es el radio de la circunferencia. Elementos de la circunferencia

15. ECUACIÓN DE LA CIRCUNFERENCIA ( C(a , b)) :
d ( P, C ) r
P ( x, y )
d ( P, C ) ( x a ) 2 ( y b) 2 r
C ( a, b)
desarrollando la ecuación......
x 2 a 2 2ax y 2 b 2 2by r2
llamando: A 2a, B 2b, C a 2 b2 r 2
x2 y 2 Ax By C 0
Ecuación general de la
circunferencia

16. Desarrollo de la ecuación

17. 4. Parábola:
Una de las cónicas. Se trata de una curva plana, abierta, que se obtiene al cortar una
superficie cónica de eje e y ángulo α mediante un plano P que no pasa por el vértice y que
corta a e bajo el mismo ángulo α.
La parábola es el lugar geométrico de los puntos
del plano que equidistan de un punto fijo
llamado foco y de una recta fija llamada directriz.
d(P,F)=d(P,s)
Elementos de la parábola
La directriz que es la recta s.
El vértice V.
El foco F.
Se llama eje de la parábola a la recta
perpendicular al eje que pasa por el foco.
La distancia entre el foco y la directriz es el
parámetro p

18. ECUACIÓN DE LA PARÁBOLA (Vértice (0,0)):
d ( P, F ) d ( P, s)
P ( x, y )
d ( P, F ) PF ( x c) 2 y2
p p
F 0, p ( x c) 2 y2 y
2 d ( P, s ) y 2
2
desarrollando la ecuación......
x2 py py
x2 2 py
Ecuación de la parábola

19. Desarrollo de la ecuación