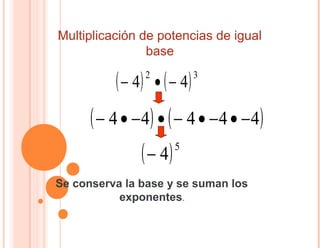
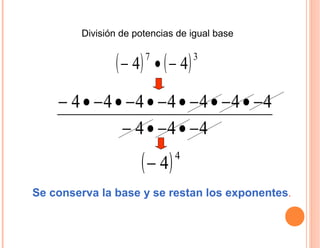
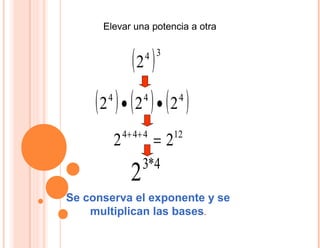
El documento describe varias propiedades de las potencias. Explica que la multiplicación de potencias de la misma base es igual a una potencia cuya base es la misma y cuyo exponente es la suma de los exponentes de los factores. También explica que la división de potencias de la misma base es igual a una potencia con la misma base y un exponente que es la diferencia entre los exponentes del dividendo y divisor. Además, describe cómo elevar una potencia a otra potencia.

1. PROPIEDADE
S DE LAS
POTENCIAS

2. ( ) ( )32
44 −•−
Multiplicación de potencias de igual
base
( ) ( )44444 −•−•−•−•−
( )5
4−
Se conserva la base y se suman los
exponentes.

3. Producto de potencias de la misma
base
Los factores del producto
Ejemplos:
42
· 45
· 43
Puede hacerse de dos modos:
El producto de potencias de la misma base es igual a una potencia con la misma
base, y de exponente la suma de los exponentes de los factores.
2. En forma de potencia, la expresión: (a) 9 · (–3)3
· (–3)
son potencias que tienen la misma base.
Modo 1º Directamente, multiplicando: = 16 · 1024 · 64 = 1048576
Modo 2º Escribiendo cada potencia como producto y agrupar después:
42
· 45
· 43
= (4 ·4) · (4 · 4 · 4 · 4 · 4) · (4 ·4 ·4) =42
· 45
· 43
42+5+3
= 410
Luego, 42
· 45
· 43
= 42+5+3
1. (–2)4
· (–2) · (–2)2
= (–2)4+1+2
= (–2)7
= –128, utilizando la propiedad vista.
Es un producto de potencias
de la misma base
2, 5 y 3 factores
–2 = (–2)1
o 61
= 6
También es igual a: 16 · (–2) · 4 = –128, haciendo los productos de las potencias.
= (–3)2
· (–3)3
· (–3) = (–3)6
Igualmente: (b) 16 · (–2)3
= (–2)4
· (–2)3
= (–2)7

4. División de potencias de igual base
( ) ( )37
44 −•−
444
4444444
−•−•−
−•−•−•−•−•−•−
( )4
4−
Se conserva la base y se restan los exponentes.

5. Cociente de potencias de la misma base
El dividendo y el divisor de
Ejercicio:
65
: 63
Puede hacerse de dos modos:
El cociente de dos potencias de la misma base es una potencia con la misma base, y con
exponente la diferencia entre los exponentes del dividendo y del divisor.
son potencias de la misma base
Modo 1º Calculando las potencias y dividiendo:
Modo 2º Desarrollando las potencias y simplificando:
65
: 63
(a) 27
: 24
= 27–4
= 23
Es un cociente de potencias
de la misma base
36
216
7776
6
6
3
5
==
252
3
5
666·6
6·6·6
6·6·6·6·6
6
6 −
===== 65
: 63
= 65–3
Caso: El cociente 54
: 54
= 1
Pero si aplicamos la propiedad 54
: 54
= 54–4
= 50
Se admite que:
50
= 1; (–7)0
= 1
Escribe en forma de potencia: (a) 27
: 24
(b) (–5)6
: (–5)3
(b) (–5)6
: (–5)3
= (–5)6-3
= (–5)3

6. Multiplicación de potencias de igual exponente
( ) ( ) ( ) ( )3333
84242 −=−•=−•
Se conserva el exponente y se
multiplican las bases.

7. División de potencias de igual exponente
( ) ( ) ( ) ( )3333
42828 −=÷−=÷−
Se conserva el exponente y se
dividen las bases.

8. Elevar una potencia a otra
( )34
2
Se conserva el exponente y se
multiplican las bases.
( ) ( ) ( )444
222 ••
12444
22 =++
4*3
2

9. Potencia de una potencia
La expresión (52
)4
es una potencia cuya base es otra potencia.
Ejercicios
Puede hacerse de dos modos:
La potencia de una potencia es igual a otra potencia con la
misma base, y de exponente el producto de exponentes.
Modo 1º Directamente, haciendo la potencia de la potencia:
Modo 2º Escribiendo como producto de potencias y agrupar después:
(52
)4
= 52
·52
· 52
· 52
= 52+2+2+2
= 52 · 4
= 58 (52
)4
=52 · 4
1. Calcula: [(–2)4
]2
Se llama potencia de una potencia
(52
)4
= (25)4
= 390625
[(–2)4
]2
= (–2)4·2
= (–2)8
= 64
2. Calcula: [(35
)4
]2
[(35
)4
]2
= 35·4·2
= 340
340
es un número
enorme: tiene
20 cifras.
3. Calcula: {[(–1)3
]9
}7
{[(–1)3
]9
}7
= (–1)3·9·7
= (–1)189
= –1

10. Elevar una potencia a un número negativo
44
2
3
3
2






=





−
Se invierte la base y se eleva al inverso aditivo del
exponente.