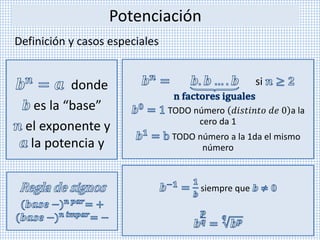
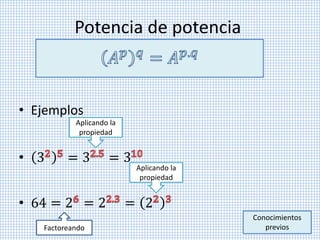
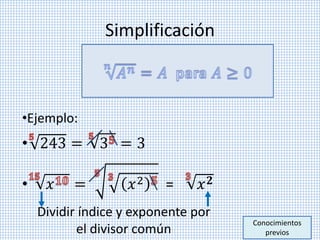
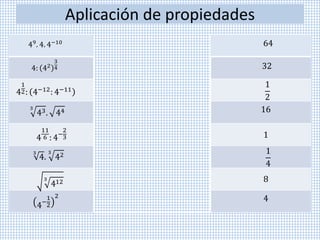
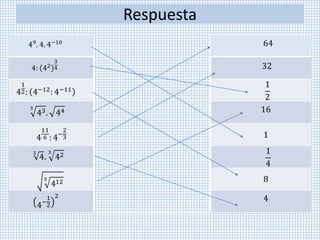
Este documento describe propiedades de potencias y radicación. Explica que los números compuestos pueden descomponerse en factores primos y define potenciación, producto y cociente de potencias de igual base, raíz de raíz, y cómo la radicación se distribuye sobre la multiplicación y división. También cubre simplificación de operaciones inversas aplicadas simultáneamente.

1. Propiedades de la potencia y
la radicación -

2. Propiedades
Potencia de potencia
Producto de potencias de igual base
• Cociente de potencias de igual base
• Raíz de raíz
• La radicación se distribuye respecto a la multiplicación
• La radicación se distribuye respeto de la división
• Los operaciones inversa aplicadas simultáneamente
se Simplifican
• Los números compuestos admiten descomposición
en factores primos

3. Los números compuestos admiten
descomposición en factores primos
• Ejemplos:
• 48 = 24
. 3 60 = 22
. 3.5 100 = 22
.52
Conocimientos
previos
NOTA: LOS NÚMEROS PRIMOS SON LOS QUE RIENEN SOLO DOS
DIVISORES NATURALES EL 1 Y SÍ MISMO: 2,3,5,7,11,13,17,19,

4. Potenciación
Definición y casos especiales
si
TODO número 𝑑𝑖𝑠𝑡𝑖𝑛𝑡𝑜 𝑑𝑒 0 a la
cero da 1
TODO número a la 1da el mismo
número
donde
es la “base”
el exponente y
la potencia y
siempre que

5. Producto de potencias de igual base
• Ejemplos:
• 7 . 7 = 7 = 7
(ya que =7.7.7.7
7
. 7.7.7.7.7
7
=7.7.7.7.7.7.7.7.7
7
)
• 2 . 2 . 2 = 2 11
• 3 =
3 = 35
. 33
3 = 32
. 36
.
Conocimientos
previos

6. Cociente de potencias de igual base
• Ejemplos:
• 7 : 7 = 7 = 7
• 2 2 = 2 2
Conocimientos
previos
ya que
7.7.7.7.7.7.7.7.7
7
7.7.7.7.7
7
=7.7.7.7
7

7. • Ejemplos
• 3 = 3 = 3
• 64 = 2 = 2 = 2
Potencia de potencia
Conocimientos
previos
Aplicando la
propiedad
Factoreando
Aplicando la
propiedad

8. La potenciación se distribuye respecto
a la multiplicación y la división:
•Ejemplos:
• 4.5 3
= 203 = 20.20.20 = 8000
43. 53 = 64.125 = 8000
Conocimientos
previos
• 10: 5 2 = 22 = 2.2 = 4
102
: 52
= 100: 25 = 4
• 4𝑚2 3 = 43(𝑚2)3= 64𝑚6
• −
𝑥
4
3
= −
𝑥3
64

9. RADICACIÓN
DEFINICIÓN COMO OPERACIÓNINVERSA DE LA POTENCIACIÓN
𝒏
𝒂 = 𝒃 𝑠𝑖 𝑦 𝑠𝑜𝑙𝑜 𝑠𝑖 𝒃 𝒏 = 𝒂
DEFINICIÓN COMO POTENCIACIÓN DE EXPONENTE FRACCIONARIO
𝒃
𝟏
𝒏 =
𝒏
𝒃
Ejemplo 1
5
−32 = −2 𝑝𝑜𝑟𝑞𝑢𝑒 −2 5
= −32
Ejemplo 2
−32
1
5 =
5
−32 = −2

10. La radicación se distribuye respecto a
la multiplicación:
•Ejemplos
•
4
. 16 =
4
16 = .2 = 6
•
3
.5 =
3
5 =
3
5
Conocimientos
previos

11. La radicación se distribuye respecto a
la división:
•Ejemplos
•
4
16
= 4
16
=
2
•
3 5
=
3
5
=
3
5
Conocimientos
previos

12. Raíz de raíz
• Ejemplos
• 7 = 7 = 7
• 7 =
7 = 7
7 = 7
… … … … … … Conocimientos
previos

13. Simplificación
•Ejemplo:
• 243 = 3 = 3
• 𝑥 = 𝑥2 = 𝑥 𝟐
Conocimientos
previos
Dividir índice y exponente por
el divisor común

14. Aplicación de propiedades
49
. 4. 4−10
4: 42
3
4
4
1
2: 4−12: 4−11
3
43. 44
3
4.
3
42
4
11
6 : 4−
2
3
3
412
4−
1
2
2 4
1
4
8
1
16
1
2
32
64

15. Respuesta
49
. 4. 4−10
4: 42
3
4
4
1
2: 4−12: 4−11
3
43. 44
3
4.
3
42
4
11
6 : 4−
2
3
3
412
4−
1
2
2 4
1
4
8
1
16
1
2
32
64