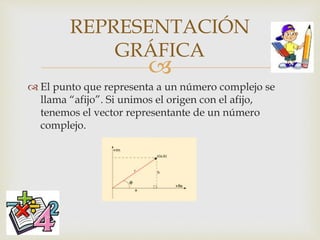
Este documento introduce los números complejos, incluyendo su representación gráfica y las operaciones básicas de suma, resta, multiplicación y división. Explica cómo representar números complejos en forma binómica y polar, y cómo convertir entre estas formas.