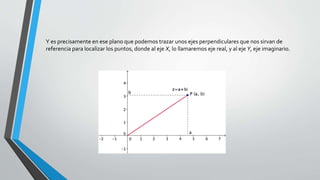
El documento describe números complejos, que pueden escribirse como a + bi, donde a es la parte real y b la parte imaginaria. Explica cómo sumar, restar, multiplicar y dividir números complejos, así como representarlos gráficamente en un plano complejo. También define el valor absoluto de un número complejo como (a2 + b2)1/2 y presenta una notación exponencial propuesta por Euler.

1. Números Complejos
Israel Ortega
Juan Pablo Chamba
Fabián Andrés Ochoa

2. Números Complejos
Un numero complejo es cualquier numero que puede escribirse en la forma
a + bi,
Donde a y b son números reales. El numero real a es la parte real, el numero real b es la parte
imaginaria y a + bi es la forma estándar
𝒊 𝟐= -1
Dos números complejos son iguales si, y solo si sus partes reales e imaginarias son iguales. Por
ejemplo
X + yi = 2 + 5i si, solo si x = 2 y y= 5

3. Operaciones con números complejos
Si a + bi y c + di son dos números complejos entonces:
• Suma: (a + bi) + (c + di) = (a + c) + ( b + d)i
• Resta: (a + bi) - (c + di) = (a - c) + ( b - d)i
• Producto por escalar: r(a, b) = (ra, rb)
• Multiplicacion: (a,b) . (c,d) = (ac – bd,ad + bc)
• Division:
(𝑎,𝑏)
(𝑐,𝑑)
=
𝑎𝑐+𝑏𝑑,𝑏𝑐 −𝑎𝑑
𝑐2+ 𝑑2 =
𝑎𝑐+𝑏𝑑
𝑐2+ 𝑑2 ,
𝑏𝑐 −𝑎𝑑
𝑐2+ 𝑑2

4. Ejercicios:
• (7 – 3i) + (4 + 5i) donde z1= 7-3i z2= 4+5i
• (2 – i) - (8 + 3i) donde z1= 2- i z2 = 8 + 3i
• (2 + 3i) . (5- i ) donde z1= 2 + 3i z2 = 5-i
•
5+𝑖
2−3𝑖
donde z1 = 5 + i z2= 2-3i

5. Representación Gráfica de Números Complejos
Los números naturales, enteros, fraccionarios y reales se pueden representar como puntos de una recta, (la
recta de los números reales).
Pero, a los Números Complejos podemos imaginarlos como puntos de un plano (el plano de los números
complejos). Esto se debe a que un número complejo en forma binómica queda determinado por un par de
números reales: su parte real, y su parte imaginaria, . De esta manera, el par representa las coordenadas
de un punto del plano. Podemos destacar que esta interpretación de los números complejos (considerarlos
puntos en un plano) se debe a Gauss y a Hamilton.

6. Y es precisamente en ese plano que podemos trazar unos ejes perpendiculares que nos sirvan de
referencia para localizar los puntos, donde al eje X, lo llamaremos eje real, y al eje Y, eje imaginario.

7. Lo habitual es utilizar las coordenadas del punto (x,y). Cuando representamos un número complejo de esta
forma decimos que está en forma cartesiana.
También se suele representar al número complejo mediante un vector de origen y extremo .
Veamos algunos ejemplos concretos:

8. Actividad
Dados los siguientes números complejos:
z1 =–1+2i ; z2 =–2–3i;
z3 =4–1i ; z4 =–5 ; z5 =3i;
Represéntalos en el plano complejo:

9. Solución

10. Valor Absoluto de un Número Complejo
• También llamado módulo de un número complejo. El módulo de un número complejo z = x + yi,
denotado como |z|, se define como (x2+y2)1/2.
• Es la distancia entre el origen y el punto que representa al número complejo.

11. Ejemplos:
El valor absoluto de 3 + 4i
(32 + 42)1/2 = 5.
Calcular los siguientes ejemplos:
• Valor absoluto de 5 + 6i
• Valor absoluto de 2 + 8i

12. Notación de Euler
En 1748 Leonhard Euler propuso la siguiente formula;
Equivalencia en forma polar a exponencial;
Z = |Z|
Z = |Z|
Operaciones en forma exponencial de Euler;
sean para: Z1 = |Z1| Z2 = |Z2|
• Multiplicación:
• División:
• Potenciación
Ejemplos:
1 2