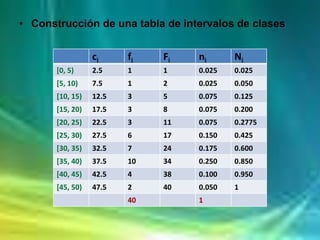
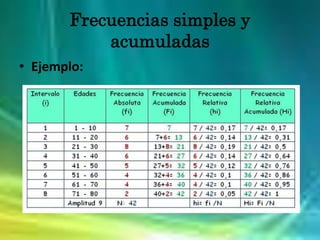
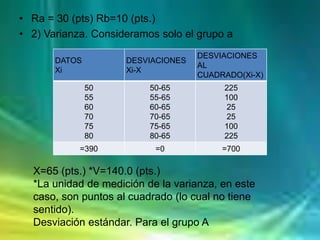
El documento presenta información sobre tablas de distribución de frecuencias, incluyendo cómo construir intervalos de clases y tablas con frecuencias simples y acumuladas. También explica conceptos estadísticos como medidas de tendencia central como la media, mediana y moda, y medidas de dispersión como la desviación estándar y varianza. Finalmente, muestra un ejemplo del cálculo de medidas de dispersión para comparar dos grupos.

1. República Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación Superior
I.U.P.S.M ‘’Santiago Mariño’’
Escuela: Ingeniería Civil
Prof:
Pedro Beltran
Bachiller:
Margeris Pastrano
C.I: 26971345
Seccion: ‘’CV’’

2. Tabla de distribución de frecuencias
• La distribución de frecuencias o tabla de frecuencias es
una ordenación en forma de tabla de los datos
estadísticos, asignando a cada dato su frecuencia
correspondiente.

3. Intervalos de Clases
• Los intervalos de clase se emplean si
las variables toman un número grande de valores o
la variable es continua.
• Se agrupan los valores en intervalos que tengan
la misma amplitud denominados clases. A cada clase se
le asigna su frecuencia correspondiente.

4. • Construcción de una tabla con Intervalos de clase
• 3, 15, 24, 28, 33, 35, 38, 42, 43, 38, 36, 34, 29, 25, 17,
7, 34, 36, 39, 44, 31, 26, 20, 11, 13, 22, 27, 47, 39, 37,
34, 32, 35, 28, 38, 41, 48, 15, 32, 13.
• 1º se localizan los valores menor y mayor de la
distribución. En este caso son 3 y 48.
• 2º Se restan y se busca un número entero un poco
mayor que la diferencia y que sea divisible por el
número de intervalos de queramos poner.
• Es conveniente que el número de intervalos oscile entre
6 y 15.
• En este caso, 48 - 3 = 45, incrementamos el número
hasta 50 : 5 = 10 intervalos.

5. • Construcción de una tabla de intervalos de clases
ci fi Fi ni Ni
[0, 5) 2.5 1 1 0.025 0.025
[5, 10) 7.5 1 2 0.025 0.050
[10, 15) 12.5 3 5 0.075 0.125
[15, 20) 17.5 3 8 0.075 0.200
[20, 25) 22.5 3 11 0.075 0.2775
[25, 30) 27.5 6 17 0.150 0.425
[30, 35) 32.5 7 24 0.175 0.600
[35, 40) 37.5 10 34 0.250 0.850
[40, 45) 42.5 4 38 0.100 0.950
[45, 50) 47.5 2 40 0.050 1
40 1

6. Numero de clases
• Es el numero de grupos en que se van a agrupar los
datos en la tabla de distribución de frecuencias. Y se
determina a través de la formula de Sturges.
•

7. Numero de clases

8. Frecuencias simples y
acumuladas

9. Frecuencias simples y
acumuladas
• Ejemplo:

10. Medidas de tendencia central
• Entre las medidas de tendencia central
tenemos:
Media aritmética
Mediana
Moda

11. Medidas de tendencia central

12. Procedimientos estadísticos al uso y
calculo de las medidas de
centralización
• Las medidas de tendencia central tienen como objetivo
el sintetizar los datos en un valor representativo, las
medidas de dispersión nos dicen hasta que punto estas
medidas de tendencia central son representativas como
síntesis de la información. Las medidas de dispersión
cuantifican la separación, la dispersión, la variabilidad de
los valores de la distribución respecto al valor central.
Distinguimos entre medidas de dispersión absolutas,
que no son comparables entre diferentes muestras y las
relativas que nos permitirán comparar varias muestras.

13. Procedimientos estadísticos al uso y
calculo de las medidas de
centralización
• La Dispersión
• Al igual que sucede con cualquier conjunto de datos, la
media, la mediana y la moda sólo nos revelan una parte
de la información que necesitamos acerca de las
características de los datos. Para aumentar nuestro
entendimiento del patrón de los datos, debemos medir
también su dispersión, extensión o variabilidad.
• La dispersión es importante porque:
 Proporciona información adicional que permite juzgar la
confiabilidad de la medida de tendencia central. Si los
datos se encuentran ampliamente dispersos, la posición
central es menos representativa de los datos.

14. Procedimientos estadísticos al uso y
calculo de las medidas de
centralización
• Medidas de tendencia central:
• Media aritmética, es la que se obtiene sumando los
datos y dividiéndolos por el número de ellos. Se aplica
por ejemplo para resumir el número de pacientes
promedio que se atiende en un turno. Otro ejemplo, es
el número promedio de controles prenatales que tiene
una gestante.
• Mediana: Corresponde al percentil 50%. Es decir, la
mediana divide a la población exactamente en dos. Por
ejemplo el número mediana de hijos en el centro de
salud “X” es dos hijos. Otro ejemplo es el número
mediana de atenciones por paciente en un consultorio.

15. Procedimientos estadísticos al uso y
calculo de las medidas de
centralización
• Moda: Valor o (valores) que aparece(n) con mayor
frecuencia. Una distribución unimodal tiene una sola
moda y una distribución bimodal tiene dos. Útil como
medida resumen para las variables nominales. Por
ejemplo, el color del uniforme quirúrgico en sala de
operaciones es el verde; por lo tanto es la moda en
colores del uniforme quirúrgico.
Medidas de dispersión
Desviación estandar: Llamada también desviación típica;
es una medida que informa sobre la media de distancias
que tienen los datos respecto de su media aritmética,
expresada en las mismas unidades que la variable.

16. Procedimientos estadísticos al uso y
calculo de las medidas de
centralización
• La varianza: Es el valor de la desviación estándar al
cuadrado; su utilidad radica en que su valor es requerido
para todos los procedimientos estadístico.
Error típico: Llamado también error estándar de la
media. Se refiere a una medida d variabilidad de la
media; sirve para calcular cuan dispersa estaría la
media de realizar un nuevo calculo.

17. • Ejemplo: Calculo de medidas de dispersión
 Supongamos que hay dos grupos de estudiantes: "
A y B ", y que ambos tienen un promedio X=65 (pts.)
de calificación, con esta información parece no
existir gran diferencia entre los dos grupos. Si
observamos los datos individuales, notamos la
diferencia:
• Grupo A Grupo B
• 50, 55, 60, 70, 75, 80, 60, 60, 60, 70, 70, 70,
• Xa=65 (pts.) Xb= 65 (pts.)
• Si calculamos las medidas de dispersión podemos
hacer un análisis mas completo entre ambos
grupos.
• Rango R =X max - Xmin.

18. • Ra = 30 (pts) Rb=10 (pts.)
• 2) Varianza. Consideramos solo el grupo a
DATOS
Xi
DESVIACIONES
Xi-X
DESVIACIONES
AL
CUADRADO(Xi-X)
50
55
60
70
75
80
50-65
55-65
60-65
70-65
75-65
80-65
225
100
25
25
100
225
=390 =0 =700
X=65 (pts.) *V=140.0 (pts.)
*La unidad de medición de la varianza, en este
caso, son puntos al cuadrado (lo cual no tiene
sentido).
Desviación estándar. Para el grupo A

19. • S= V = 140.0 = 11.83
• S=11.83(pts.)
• * La desviación estándar para el grupo B es: S= 5.48
(pts.)
• Resumiendo los cálculos anteriores:
• Con estas medidas descriptivas podemos establecer
mejores conclusiones que con los datos solamente, o
los promedios es necesario calcular siempre una medida
de tendencia, generalmente la media (X), y una medida
de dispersión, el rango (R) o la desviación estándar (S).
• En el ejemplo anterior la medida de dispersión a utilizar
es el rango (R), por la cantidad de datos.
GRUPO A GRUPO B
X=65pts.
R=30pts.
X=65pts.
R=10pts.
S=11.83 S=5.48

20. Bibliografía
• http://html.rincondelvago.com/estadistica_51.html
• http://eduteka.icesi.edu.co/proyectos.php/1/3053
• https://es.wikipedia.org/wiki/Medidas_de_tendencia_cent
ral