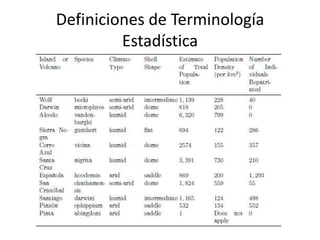
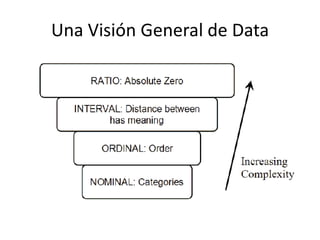
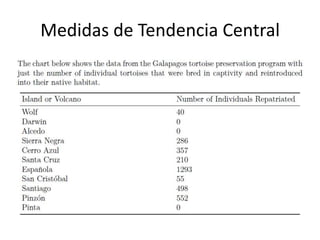
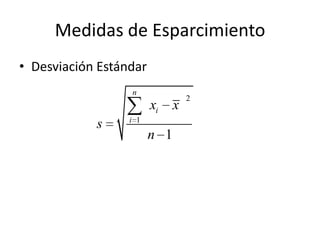
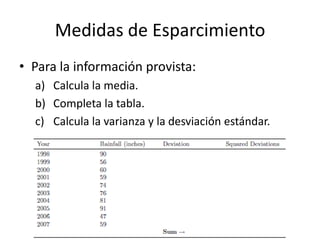
Este documento introduce conceptos estadísticos básicos como población, muestra, variables, niveles de medición, medidas de tendencia central y esparcimiento. Explica que una población es el grupo total estudiado, mientras una muestra es un subgrupo representativo. Las variables pueden ser categóricas, discretas, continuas u ordinales. Las medidas de tendencia central incluyen la moda, media y mediana, mientras las medidas de esparcimiento son el rango e IQR.

1. Introducción al Análisis de Data EstadísticaProbabilidad y Estadística

2. Definiciones de Terminología Estadística

3. Definiciones de Terminología Estadística

4. Definiciones de Terminología EstadísticaClasificando VariablesPoblaciónEs el grupo entero que se está estudiando.UnidadCada miembro de la población.VariablesCaracterísticas de las cuales se recoge información.Tipos de variablesCategóricas (Cualitativas)Numéricas (Cuantitativas)

5. Definiciones de Terminología Estadística

6. Definiciones de Terminología EstadísticaLas variables también se pueden clasificar como:DiscretaContinua

7. Definiciones de Terminología EstadísticaPoblación vs. MuestraMuestraGrupo representativo de la poblaciónParámetroValor real de la variable de una poblaciónEstadístico (a)Estimado de un parámetro basado en la muestra

8. Definiciones de Terminología EstadísticaErrores en Muestreo“Sampling error”La diferencia potencial entre el parámetro verdadero y la estadística obtenida al utilizar la muestra.“Bias”Cuando se favorece, voluntaria o involuntariamente, algún resultado en particular.

9. Definiciones de Terminología Estadística

10. Definiciones de Terminología Estadística

11. Definiciones de Terminología Estadística

12. Una Visión General de DataNiveles de MedidaNominalOrdinalIntervaloRatio (Razón)

13. Una Visión General de DataMedida NominalEste es el tipo de medidas en el cual los valores de las variables son nombres y no del todo numéricos.Medida OrdinalEste tipo de medida envuelve recolectar información en el cual el orden es en alguna forma significativoEn la medida ordinal, la distancia entre dos valores consecutivos no tiene significado.

14. Una Visión General de DataMedida de IntervaloEn este tipo de medida, además de dar un orden como en la medida ordinal, le da significado a la distancia entre dos valores cualesquiera.Medida de Ratio (Razón)Este tipo de medida incluye los conceptos de orden e intervalo, como en la medida de intervalo, pero añade la idea de “la nada” o cero absoluto.

15. Una Visión General de DataEjemplo: Supongamos que la escuela quiere recolectar información (data) sobre todos los estudiantes en la escuela.Nominal: Podemos recolectar información sobre el genero de los estudiantes, pueblo en el que viven, raza u opiniones políticas.Ordinal: Podemos recolectar data sobre el grado en que se encuentran los estudiantes.Intervalo: Podemos recolectar data de los resultados de CollegeBoard en la parte de matemáticas.Ratio: Data sobre la edad, peso y altura de los estudiantes.

16. Una Visión General de Data

17. Una Visión General de DataEstudios ObservacionalesEn un estudio observacional, el investigador observa la población de interés y anota los resultados sin hacer intento alguno de controlar los resultados.Un estudio observacional de periodo largo en el cual el grupo de sujetos es observado por largos periodos de tiempo es llamado un estudio longitudinal.

18. Una Visión General de DataExperimentosEn un experimento, el investigador impone un tratamiento en un grupo de sujetos en un esfuerzo por determinar una relación “causa y efecto” entre las variables.En este método el investigador necesitará asegurarse que cualquier otra cosa que pueda influenciar la variable a ser investigada sea controlada.

19. Una Visión General de DataMedidas de Centro y EsparcimientoSi queremos utilizar un número o valor para resumir la data, podemos mirar hacia donde la data está centrada.Las variables que son medidas a nivel nominal pueden ser resumidas fácilmente identificando el valor más común (moda)Las variables que son medidas a nivel de ratio se pueden resumir utilizando el promedio (media) o el número del medio (mediana)

20. Una Visión General de DataMedidas de Centro y EsparcimientoOtro elemento importante del conjunto de data es como esta esparcida.Otras medidas que nos brindan información sobre el esparcimiento los son:Rango intercuartilDesviación estándar

21. Una Visión General de Data

22. Una Visión General de Data

23. Una Visión General de Data

24. Medidas de Tendencia CentralModaLa moda se define como el número que más frecuentemente aparece en un conjunto de data.La moda es más útil en situaciones que envuelven data categórica (cualitativa) que es medida al nivel nominal.EjemploSe le preguntó a los estudiantes en la clase de estadística que dijeran cuantos niñ@s viven en sus casa. La data es la siguiente: 1, 3, 4, 3, 1, 2, 2, 2, 1, 2, 2, 3, 4, 5, 1, 2, 3, 2, 1, 2, 3, 6Dos asuntos con la modaBimodal“No hay moda”

25. Medidas de Tendencia Central MediaMedia es el nombre que los estadísticos le dan a lo que comúnmente conocemos como promedio.La media es “el punto de balance” numérico del conjunto de datos.

26. Medidas de Tendencia Central

27. Medidas de Tendencia CentralEjemplo con bloques.Ejemplo con calculadora.

28. Medidas de Tendencia CentralMedianaLa mediana es el número que está en medio de un conjunto de data.Ejemplos:80, 94, 75, 90, 9691, 83, 97, 89

29. Medidas de Tendencia Central“Outliers” y Resistencia“Outliers” o valores atípicos son valores extremos, ya sean muy grandes o pequeños.La media es afectada por la presencia de un “outlier”, pero la mediana no.Una estadística que no es afectada por los “outliers” es llamada resistente.

30. Medidas de Tendencia CentralMedia de la Población vs. Media de la Muestra

31. Medidas de Tendencia CentralOtras medidas de Tendencia CentralMidrangeEs la media de los valores máximos y mínimos del conjunto de data Trimmed MeanEs la media de los datos removiendo los valores máximo y el mínimo.n% Trimmed MeadEs la media cuando se remueve un porciento específico de los datos, la mitad a cada lado.

32. Medidas de Tendencia CentralEncuentra el midrange y el trimmed mean de los siguientes datos:94, 80,75, 96, 90Encuentra el 20% trimmed mean de los siguientes datos:1, 3, 4, 3, 1, 2, 2, 2, 1, 2, 2, 3, 4, 5, 1, 2, 3, 2, 1, 2, 3, 6

33. Medidas de Tendencia CentralWeighted Mean (Media Ponderada)Este es un método de calcular la media cuando algunos de los datos se cuentan frecuentemente.Se multiplica la frecuencia de cada dato por el valor del dato se suman y se divide entre la cantidad de datos.Determina la media para los siguientes datos utilizando weighted mean.1, 3, 4, 3, 1, 2, 2, 2, 1, 2, 2, 3, 4, 5, 1, 2, 3, 2, 1, 2, 3, 6

34. Medidas de Tendencia CentralPercentiles y CuartilesUn percentil es un estadístico, que identifica el porciento de la data que es menor que el valor dado.La mediana es el percentil 50.Dos percentiles usados comúnmente son el percentil 25 y el 75 y se le refiere a estos como cuartil inferior (Q1) y cuartil superior (Q3).Encuentra Q1, Q2y Q3 para los siguientes datos: 73, 75, 80, 84, 90, 92, 93, 94, 96

35. Medidas de Tendencia CentralMedianas y Cuartiles en la Calculadora Gráfica

36. Medidas de Tendencia Central

37. Medidas de Tendencia CentralPara esta data, calcula lo siguiente:ModaMedianaMedia10% trimmed meanMidrangeQ1 y Q3

38. Medidas de EsparcimientoRangoEs la diferencia entre el valor mínimo y el valor máximo.Rango Intercuartil (IQR)Es la diferencia entre los cuartiles.

39. Medidas de EsparcimientoDetermina el rango y el IQR de la data.

40. Medidas de EsparcimientoDesviación EstándarLa desviación estándar es una medida de esparcimiento que se basa en la media, esta nos da información sobre cuan lejos están los datos de la media.La diferencia entre el valor actual y la media es llamada desviación.

41. Medidas de EsparcimientoEjemplo;Seleccionamos al azar a tres personas y le preguntamos su tamaño de zapato. 9½, 11½ y 12La media es 11.La suma de las desviaciones siempre va a dar a cero.

42. Medidas de EsparcimientoSuma de las desviaciones cuadradas = 3.5Este resultado se divide entre n – 1; lo que nos da lo que se conoce como la varianza.Por último le tomamos la raíz cuadrada a la varianza y obtenemos la desviación estándar.

43. Medidas de EsparcimientoDesviación Estándar

44. Medidas de EsparcimientoPara la información provista:Calcula la media.Completa la tabla.Calcula la varianza y la desviación estándar.