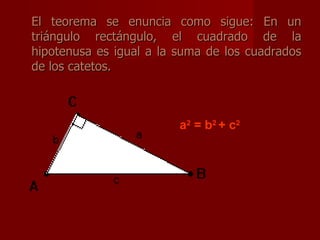
El documento describe el Teorema de Pitágoras y varias demostraciones posibles de este teorema. Explica que el teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. A continuación, presenta brevemente algunas de las demostraciones históricas del teorema, incluyendo las de Pitágoras, Anaricio, Liu Hui, Perigal y Ozanam.

1. EL TEOREMA DE PITAGORAS Y SUS MULTIPLES DEMOSTRACIONES

2. 1. DESCRIPCIÓN DEL PROBLEMA Suele ocurrir que la expresión a 2 = b 2 + c 2 es usada por los estudiantes sin comprender su verdadero sentido geométrico, existen varias demostraciones de tal teorema; mucho de estas consisten en rompecabezas los cuales se pueden usar en primaria como simples juegos para trabajar equivalencias de superficies, y en secundaria como complemento a las comprobaciones numéricas y demostraciones algebraicas.

3. El teorema se enuncia como sigue: En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. a 2 = b 2 + c 2

4. A continuación daremos a conocer algunas de las demostraciones de este famoso teorema. PITÁGORAS. ANARICIO LIU HUI

5. PERIGAL OZANAM Triangulo Rectángulo Isósceles [1] [1] La primera figura es aporte de PLATÓN.