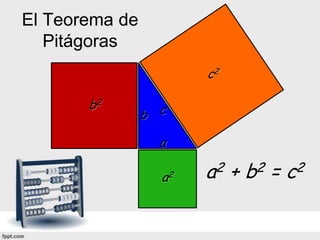
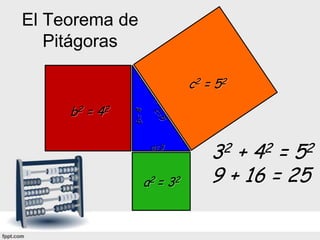
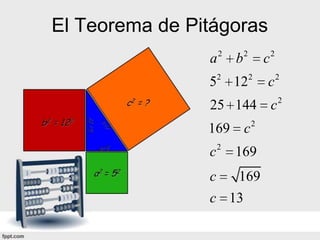
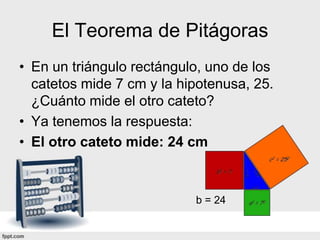
El documento explica qué es la trigonometría y el Teorema de Pitágoras. El Teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. El documento proporciona ejemplos de cómo aplicar el Teorema para calcular lados desconocidos y determinar qué triángulos son rectángulos. También discute las "ternas pitagóricas", que son conjuntos de tres números que cumplen la propiedad del Teorema y represent

1. G. Edgar Mata Ortiz

2. ¿Qué es trigonometría?
• La trigonometría es una rama de la
matemática, cuyo significado etimológico
es "la medición de los triángulos". Deriva
de los términos griegos τριγωνο trigōno
triángulo y μετρον metron medida.
• Wikipedia

3. El Teorema de Pitágoras
• Teorema de Pitágoras
• En todo triángulo rectángulo el cuadrado
de la hipotenusa es igual a la suma de los
cuadrados de los catetos.
Pitágoras de Samos

4. El Teorema de
Pitágoras
c2
b2
b c
a
a2 a 2 + b2 = c 2

5. El Teorema de
Pitágoras
c2 = 5 2
b2 = 42
b= 4
a=3
3 2+ 4=2 5 2
a2 = 32 9 + 16 = 25

6. El Teorema de Pitágoras
• Un aspecto interesante del
teorema de Pitágoras es que
funciona en dos sentidos:
• “Si un triángulo es rectángulo, sus
lados cumplen con la propiedad
señalada”
• “Si en un triángulo los lados
cumplen con la propiedad
indicada, entonces dicho triángulo
es rectángulo”

7. El Teorema de Pitágoras
• Veamos algunos ejemplos:
• “Si un triángulo es rectángulo, sus lados
cumplen con la propiedad señalada”
• En un triángulo rectángulo, los catetos
miden 5 y 12 cm respectivamente,
¿cuánto mide la hipotenusa?

8. El Teorema de Pitágoras
2 2 2
a b c
2 2 2
5 12 c
2
25 144 c
169 c 2
c 2 169
c 169
c 13

9. El Teorema de Pitágoras
• En un triángulo rectángulo, los catetos
miden 5 y 12 cm respectivamente,
¿cuánto mide la hipotenusa?
c = 13
• Ya tenemos la respuesta:
• La hipotenusa mide 13 cm.

10. El Teorema de Pitágoras
• Este procedimiento puede aplicarse para
calcular la hipotenusa si se conocen los
catetos o para determinar uno de los
catetos si se conoce la hipotenusa y el
otro cateto.
• Sólo es necesario despejar.

11. El Teorema de Pitágoras
• En un triángulo rectángulo, uno de los
catetos mide 7 cm y la hipotenusa, 25.
¿Cuánto mide el otro cateto?
Va a ser necesario
despejar.
*EL cateto conocido
puede ser identificado
por cualquiera de las
incógnitas a ó b.

12. El Teorema de Pitágoras
2 2 2
a b c
72 b2 252
49 b 2 625
b2 625 49
2
b 576
b 576
b 24

13. El Teorema de Pitágoras
• En un triángulo rectángulo, uno de los
catetos mide 7 cm y la hipotenusa, 25.
¿Cuánto mide el otro cateto?
• Ya tenemos la respuesta:
• El otro cateto mide: 24 cm
b = 24

14. El Teorema de Pitágoras
• Habíamos comentado que el
teorema de Pitágoras es funciona
en dos sentidos:
• “Si un triángulo es rectángulo, sus
lados cumplen con la propiedad
señalada”
• “Si en un triángulo los lados
cumplen con la propiedad
indicada, entonces dicho triángulo
es rectángulo”

15. El Teorema de Pitágoras
• Veamos ahora como aplicar la segunda
afirmación
• “Si en un triángulo los lados cumplen con
la propiedad indicada, entonces dicho
triángulo es rectángulo”
• Ejemplo

16. El Teorema de Pitágoras
• Determina cuáles de las siguientes ternas
de números son los lados de un triángulo
rectángulo:
A. 12, 36, 37
B. 12, 35, 37
C. 20, 21, 29
D. 20, 22, 29

17. El Teorema de Pitágoras
• Para elegir las ternas correctas deben
cumplir con:
• La suma de los cuadrados de los catetos
es igual al cuadrado de la hipotenusa.
A. 12, 36, 37
B. 12, 35, 37
C. 20, 21, 29
D. 20, 22, 29

18. El Teorema de Pitágoras
• Elevamos al cuadrado cada terna
y verificamos que cumplan con
dicha propiedad:
A. 12, 36, 37: ¿144 + 1296 = 1369?
B. 12, 35, 37: ¿144 + 1225 = 1369?
C. 20, 21, 29: ¿400 + 441 = 841?
D. 20, 22, 29: ¿400 + 484 = 841?

19. El Teorema de Pitágoras
• Solamente los incisos B y C cumplen
con la propiedad señalada, por lo
tanto, son las ternas que son los
lados de triángulos rectángulos.
A. 12, 36, 37: ¿144 + 1296 = 1369?
B. 12, 35, 37: ¿144 + 1225 = 1369?
C. 20, 21, 29: ¿400 + 441 = 841?
D. 20, 22, 29: ¿400 + 484 = 841?

20. Ternas Pitagóricas
• Nos hemos estado refiriendo a
grupos de tres números que
sean los lados de un triángulo
rectángulo.
• Estos grupos de tres número
se llaman ternas Pitagóricas y
son motivo de numerosas
investigaciones en
matemáticas.

21. Ternas Pitagóricas
• Algunos sitios interesantes acerca de
ternas Pitagóricas son:
• http://gaussianos.com/generando-ternas-pitagoricas/
• http://www.disfrutalasmatematicas.com/geometria/pitagoricas-ternas.html
• http://www.astroseti.org/articulo/3626/
• Tablilla Babilónica Plimpton 322. Primeras ternas Pitagóricas de la
historia

22. licmata@hotmail.com
http://licmata-math.blogspot.com/