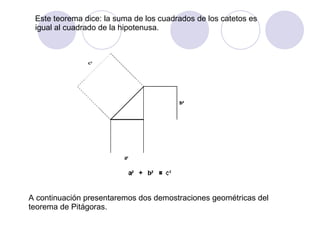
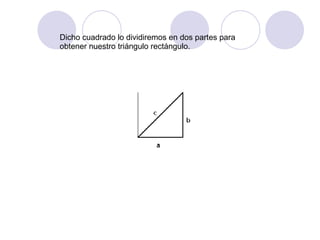
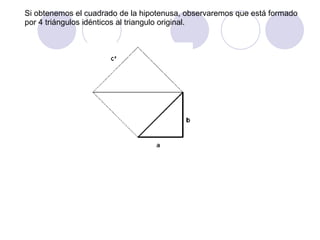
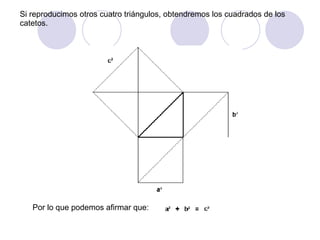
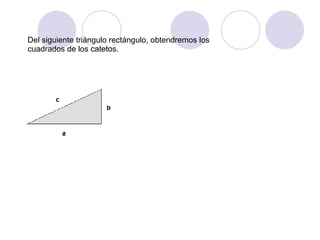
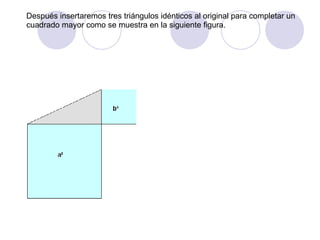
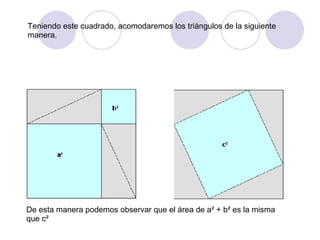
El documento presenta dos demostraciones geométricas del teorema de Pitágoras, el cual establece que la suma de los cuadrados de los catetos de un triángulo rectángulo es igual al cuadrado de la hipotenusa. La primera demostración se aplica a triángulos rectángulos donde los catetos son iguales y la segunda a triángulos donde los catetos son desiguales. Ambas demostraciones utilizan figuras geométricas para ilustrar que el área del cuadrado formado por la hipoten

1. Teorema de Pitágoras.

2. A continuación presentaremos dos demostraciones geométricas del teorema de Pitágoras. Este teorema dice: la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

3. Demostración 1 Esta demostración se aplica en un triángulo rectángulo donde los catetos tienen el mismo valor, es decir: a = b

4. Primero tenemos un cuadrado

5. Dicho cuadrado lo dividiremos en dos partes para obtener nuestro triángulo rectángulo.

6. Si obtenemos el cuadrado de la hipotenusa, observaremos que está formado por 4 triángulos idénticos al triangulo original.

7. Si reproducimos otros cuatro triángulos, obtendremos los cuadrados de los catetos. Por lo que podemos afirmar que:

8. Demostración 2 Esta demostración se aplica para triángulos rectángulos donde los catetos tienen distinto valor, es decir: a ≠ b

9. Del siguiente triángulo rectángulo, obtendremos los cuadrados de los catetos.

10. Después insertaremos tres triángulos idénticos al original para completar un cuadrado mayor como se muestra en la siguiente figura.

11. Teniendo este cuadrado, acomodaremos los triángulos de la siguiente manera. De esta manera podemos observar que el área de a ² + b ² es la misma que c²

12. Gracias por su atención Esta creación original ha sido presentada por: Jaime Sierra. Ortiz Rodríguez. Ruelas Soto. Valencia González. Con la participación especial de: Orberto. *Esta penado el uso de este material para fines no educativos o lucrativos.