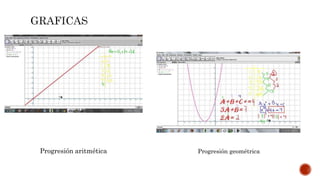
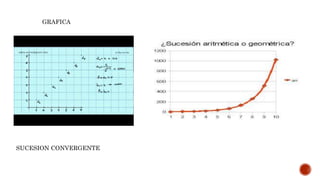
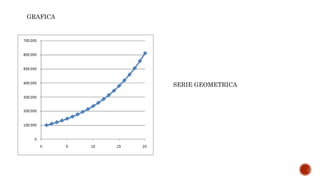
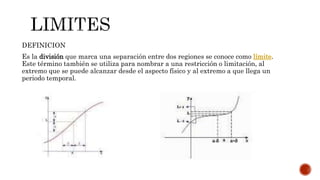
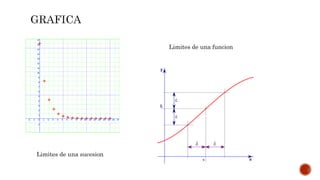
El documento define y clasifica sucesiones matemáticas, distinguiendo entre progresiones aritméticas y geométricas, así como sucesiones finitas, infinitas, convergentes, divergentes y oscilantes. También se introducen conceptos de series, como series convergentes y divergentes, además de diferentes tipos de series, incluidos las armónicas y geométricas. Se enfatiza la diferencia entre sucesiones y series, señalando que una serie es la suma de los términos de una sucesión.

1. PRESENTADO POR:
ANA MARIA NAVARRO BOTERO
11-2

2. DEFINICION
Es una sucesión de números que la diferencia de dos términos sucesivos cual quiera es la
secuencia de una constante, cantidad llamada diferencia de la progresión, diferencia o incluso
distancia.

3. Progresiones aritmeticas
Se trata de una secuencia formada por elementos
sucesivos, obtenidos mediante la suma del
elemento previo por un valor constante.
La secuencia 3, 7, 11, 15, 19 es una progresión
aritmética cuya diferencia constante es 4.
Progresiones geometricas
Se trata de una secuencia formada por elementos
sucesivos, obtenidos mediante la multiplicación del
elemento previo por un valor constante.
Progresión geométrica con factor -3: 8; -24; 72; -216.
Progresión geométrica con factor 1,5: 2; 3; 4,5; 6,75.
 Cabe destacar, por último, que si el factor es 1, la
progresión geométrica será constante.

4. Progresión aritmética Progresión geométrica

5. • El primer término de una progresión aritmética es -1, y el
décimoquinto es 27. Hallar la diferencia y la suma de los
quince primeros términos.
a 1 = − 1; a 15 = 27;
a n = a 1 + (n - 1) · d
27= -1 + (15-1) d;
28 = 14d;
d = 2
R/: -1;+1;+3;+5;+7;+9;+11;+13;+15;+17;+19;+21;+23,+25;+27….

6. DEFINICION
Una sucesión matemática es una aplicación cuyo dominio es el conjunto de los números
naturales y su codominio es cualquier otro conjunto, generalmente de números, figuras
geométricas o funciones.
 Se llama sucesión a un conjunto de números dispuestos uno a continuación de otro.
a1, a2, a3 ,..., an
3, 6, 9,..., 3n
Los números a1, a2 , a3 , ...; se llaman términos de la sucesión.
El subíndice indica el lugar que el término ocupa en la sucesión.
El término general es an es un criterio que nos permite determinar cualquier término de la
sucesión.

7.  Sucesión finita: es una serie de elementos que tienen un final. El primer y último número ya están
definidos.
 Sucesión infinita: son aquellas sucesiones que no tienen un final y siempre se distinguen por ir seguido de
los tres puntos (...).
 Sucesiones convergentes: Este tipo
corresponde a las sucesiones con límite finito.
Podemos decir que converge a '0' o a '1'.
La sucesión an = 1/n converge a 0.
Por ejemplo: 1, 1/2, 1/3, 1/4, 1/5..., 1/n
La sucesión an = n/n+1 converge a
1.
Por ejemplo: 1/2, 2/3, 3/4, 4/5, ...,
n/n+1
 Sucesiones divergentes: Este tipo de sucesión
algebraica es de límite infinito. Se representa con
el símbolo del infinito (∞) o tres puntos
suspensivos.
La fórmula es 2n+3,
por ejemplo: 5, 7, 9, 11, 13, 2n+3

8.  SUCESIONES OSCILANTES
Estas sucesiones no son ni convergentes, ni divergentes, se alterna de mayor a menor y viceversa.
Por ejemplo: 1, 0, 3, 0, 5, 0, 7, ...
 SUCESIONES ALTERNADAS
Estas sucesiones hacen a su vez otra clasificación de sucesiones numéricas- convergentes, divergentes y oscilantes- y
son aquellas que alternan los signos de sus términos o números.
1. Sucesiones alternadas convergentes: Son
aquellas que tienen límite=0 sean pares o
impares. 1, −1, 0.5, −0.5, 0.25, −0.25, 0.125,
−0.125,..
2. Sucesiones alternadas divergentes: cuando
tanto términos pares o impares su límite=∞.
1, 1, 2, 4, 3, 9, 4, 16, 5, 25, …
3. Sucesiones alternadas oscilantes: son las series
en las que se cumple la siguiente fórmula: (−1)n
n
−1, 2, −3, 4 ,−5, …, (−1)n n

9. Las sucesiones monótonas se clasifican en sucesiones monótonas crecientes y decrecientes. Por tanto,
estas series numéricas se dan cuando los términos de la sucesión crecen y decrecen.
 Crecientes: sería cuando cada uno de los
números es igual o menor que el que le
sigue.
Creciente: an < ó = an +1 Y an+1 ≥ an 2, 2 ,
4, 4, 8, 8,...
2 ≥ 2; 4 ≥ 2; 4 ≥ 4; .
 Estrictamente creciente: Se dice que una
sucesión es estrictamente creciente si cada
término es mayor que el anterior. an+1 >
an
2, 5, 8, 11, 14, 17,...
5 > 2; 8 > 5; 11 > 8; ...
• Decreciente: lo contrario, cuando los números son
mayores o iguales que el siguiente
Decreciente: an > ó = an+ 1
• Estrictamente decrecientes: Se dice que una
sucesión es estrictamente decreciente si cada
término de la sucesión es menor que el anterior.
an+1 < an
1, 1/2, 1/3, 1/4, 1/5, 1/6,...
1/2 < 1; 1/3 < 1/2 ; 1/4 < 1/3; ..

10.  SUCESIONES ARITMETICAS
Esta sucesión tiene una diferencia de 3
entre cada dos términos.
La regla es xn = 3n-2
1, 4, 7, 10, 13, 16, 19, 22, 25, ...
 SUCESIONES ESPECIALES
CUBICA
El siguiente número se calcula
elevando al cubo su posición.
La regla es xn = n3
1, 8, 27, 64, 125, 216, 343, 512, 729, …
 SUCESIONES GEOMETRICAS
Esta sucesión tiene un factor 2 entre
cada dos términos.
La regla es xn = 2n
2, 4, 8, 16, 32, 64, 128, 256, …
 SUCESIONES ESPECIALES
CUADRATICA
El siguiente número se calcula
elevando al cuadrado su posición.
La regla es xn = n2
1, 4, 9, 16, 25, 36, 49, 64, 81, …

11. GRAFICA
SUCESION CONVERGENTE

12.  an = 1, 2, 3, 4, 5, ...n
Es creciente.
Está acotada inferiormente
Cotas inferiores: 1, 0, -1, ...
El mínimo es 1.
No está acotada superiormente.
Divergente
 an= 2, -4, 8, -16, 32, ..., (-1)n-1 2n
No es monótona.
No está acotada.
No es convergente ni divergente.

3, 4/3, 1, 6/7,...
Es monotona estrictamente
decreciente.
a1= 3; a3= 1
a1000= 0.5012506253127
a1000 000 = 0.5000012500006
El límite es 0.5

13. DEFINCION
"Sucesiones" y "series" pueden parecer la misma cosa... pero en realidad
una serie es la suma de una sucesión.
Sucesión: {1,2,3,4}
Serie: 1+2+3+4 = 10
Las series se suelen escribir con el símbolo Σ que significa "súmalos
todos
":

14.  Las series pueden ser :
divergentes (cuando la suma es infinita)
convergentes (cuando la suma se aproxima a un valor real).
 SERIE ARMONICA
Es una serie divergente.
Una serie alternada es una serie
donde los términos cambian de signo
TIPOS DE SERIES ARMONICAS:
• Serie armónica alternada: La serie
armónica alternada, sin embargo,
converge. Esta es una consecuencia de la
serie de Taylor del logaritmo natural.
• Serie armónica parcial.

15.  SERIE GEOMETRICA
es una serie en la cual cada término se
obtiene multiplicando el anterior por
una constante, llamada razón r. En
este ejemplo, con r = 1/2):
 SERIE ALTERNADA.
es una serie infinita. con an ≥ 0. Una
suma finita de este tipo es una suma
alternada. Una condición suficiente
para que la serie alternada converja es
que sea absolutamente convergente
 SERIE TELOSCOPICA
Es la suma donde an = bn − bn+1
La convergencia de dicha serie y su
suma se pueden calcular fácilmente,
ya que:
 SERIE HIPERGEOMETRICA
Una serie hipergeométrica es una
serie de la forma
con =

16. GRAFICA
SERIE GEOMETRICA

17. DEFINICION
Es la división que marca una separación entre dos regiones se conoce como límite.
Este término también se utiliza para nombrar a una restricción o limitación, al
extremo que se puede alcanzar desde el aspecto físico y al extremo a que llega un
periodo temporal.

18.  LIMITES FINITOS EN EL
INFINITO
Se dice que una función tiene limite b
cuando x tiende a +∞ cuando la
función se acerca a b cuando la x se
hace cada vez mayor, es decir:
lımx→∞ f(x) = b
En este caso el limite es 2 cuando x
tiende a +∞. De igual modo se define el
limite finito cuando x tiende a −∞.
 LIMITES INFINITOS EN EL INFINITO
Aparece este caso cuando si x tiende a +∞ la
función se hace cada vez mayor o menor (lo
mismo si x tiende a −∞).
En este caso: lımx→∞ f(x) = −∞
 LIMITES DE POLINOMIOS
El limite de cualquier polinomio cuando x tiende a ∞ siempre
es +∞ o −∞, dependiendo del coeficiente del termino de mayor
grado del polinomio:
lımx→∞(2x5 − 3x2 + 5) = +∞
lımx→∞(−3x7 − 5x2 + 4x − 8) = −∞

19. Limites de una sucesion
Limites de una funcion

20. 