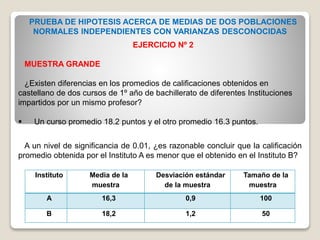
Este documento presenta cuatro ejercicios resueltos de pruebas de hipótesis. El primer ejercicio compara los tiempos de secado promedio de dos fórmulas de pintura. El segundo analiza las calificaciones promedio de dos cursos de bachillerato. El tercero compara los flujos de corriente promedio de dos diseños de microcircuitos. Y el cuarto compara la resistencia promedio al impacto de engranes de dos proveedores. Cada ejercicio presenta los datos, la prueba de hipótesis aplicada y la conclusión

1. EJERCICIOS RESUELTOS DE PRUEBA DE HIPOTESIS
PROFESOR DEL CURSO DE ESTADISTICA APLICADA:
ANTONIO IZQUIERDO ESPINOZA
ALUMNO:
JHONNY FRANCISCO REAÑO SILVA

2. EJERCICIO Nº 1
Un diseñador de productos está interesado en reducir el tiempo de
secado de una pintura. Se prueban dos formulas de pintura; la formula 1
tiene el contenido químico estándar y la formula 2 tiene un nuevo
ingrediente secante que tiende a reducir el tiempo de secado. De la
experiencia se sabe que la desviación estándar del tiempo de secado es
8 minutos y esta variabilidad inherente no debe verse afectada por la
adición del nuevo ingrediente.
Se pintan 35 placas con la formula 1 y otras 35 con la fórmula 2. Los
dos tiempos promedio de secado muéstrales son 116 minutos para la
formula 1 y 112 minutos para la formula 2 ¿a qué conclusión puede llegar
el diseñador del producto sobre la eficacia del nuevo ingrediente, al nivel
de significancia 0,01?
PRUEBA DE HIPOTESIS ACERCA DE MEDIAS DE DOS POBLACIONES
NORMALES INDEPENDIENTES CON VARIANZAS CONOCIDAS

3. Resp : El tiempo de secado es menor con la formula antigua, por lo tanto
no hay evidencia que indique que la nueva fórmula sea más eficaz que la
antigua.

4. Instituto Media de la
muestra
Desviación estándar
de la muestra
Tamaño de la
muestra
A 16,3 0,9 100
B 18,2 1,2 50
EJERCICIO Nº 2
MUESTRA GRANDE
¿Existen diferencias en los promedios de calificaciones obtenidos en
castellano de dos cursos de 1º año de bachillerato de diferentes Instituciones
impartidos por un mismo profesor?
 Un curso promedio 18.2 puntos y el otro promedio 16.3 puntos.
A un nivel de significancia de 0.01, ¿es razonable concluir que la calificación
promedio obtenida por el Instituto A es menor que el obtenido en el Instituto B?
PRUEBA DE HIPOTESIS ACERCA DE MEDIAS DE DOS POBLACIONES
NORMALES INDEPENDIENTES CON VARIANZAS DESCONOCIDAS

5. Resp : La calificación promedio obtenida por el instituto A es menor
que el obtenido en el instituto B.

6. Diseño 1 n1 = 16 s1
2 = 10
Diseño 2 n2 = 10 s2
2 = 40
EJERCICIO Nº 3
MUESTRA PEQUEÑA
Un fabricante de monitores prueba dos diseños de microcircuitos para
determinar si producen un flujo de corriente equivalente. El departamento de
ingeniería ha obtenido los datos siguientes:
Con nivel de significancia 0.05, se desea determinar si existe alguna
diferencia significativa en el flujo de corriente promedio entre los dos diseños,
donde se supone que las dos poblaciones son normales, pero no es posible
suponer que las varianzas desconocidas sean iguales.

7. Resp : No existe diferencia significativa en el flujo de corriente promedio
entre los dos diseños.

8. EJERCICIO Nº 4
Dos proveedores fabrican un engrane de plástico utilizado en una impresora
láser. Una característica importante de estos engranes es la resistencia al
impacto la cual se mide en pies-libras. Una muestra aleatoria de 10 engranes
suministrados por el primer proveedor arroja los siguientes resultados:
y s1 = 12. Del segundo proveedor se toma una muestra aleatoria de 16
engranes, donde los resultados son
y s2 = 45. ¿Existe evidencia que apoye la afirmación de que los engranes del
proveedor 2 tienen una mayor resistencia promedio al impacto. Use un nivel de
significancia de 0.05.

9. Resp : El promedio de resistencia de los engranes del proveedor 2 es
mayor al del proveedor 1.

10. GRACIAS !