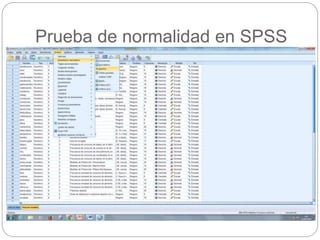
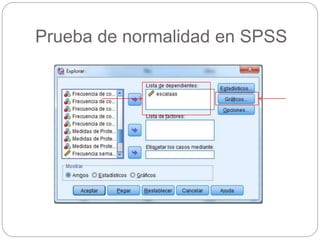
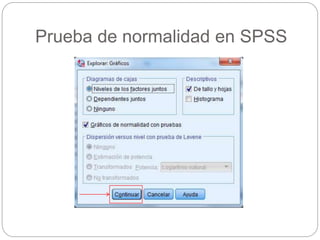
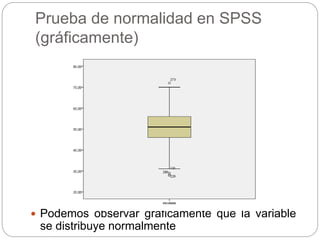
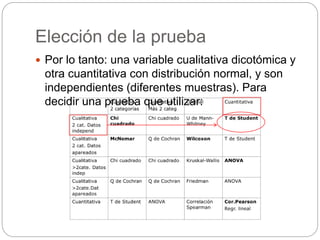
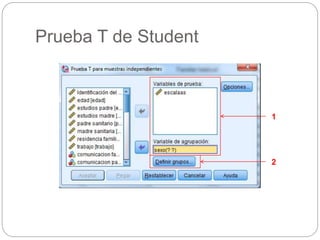
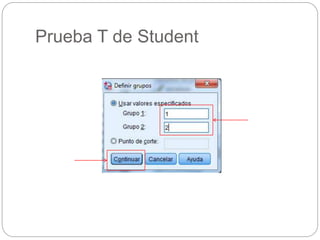
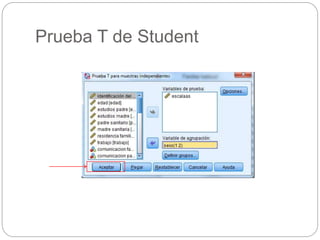
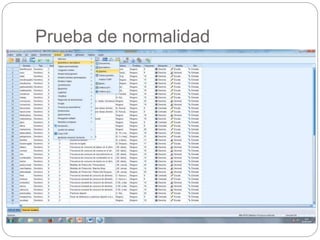
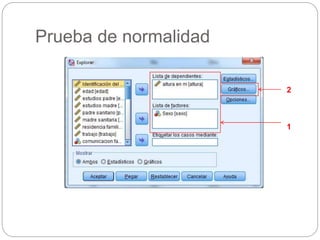
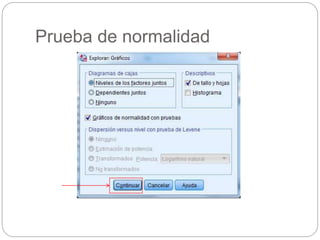
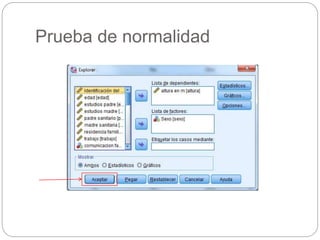
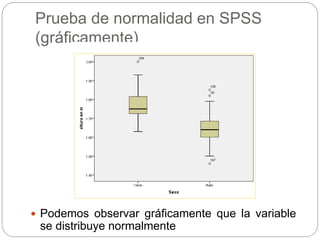
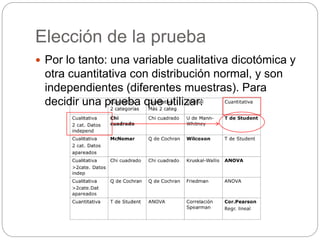
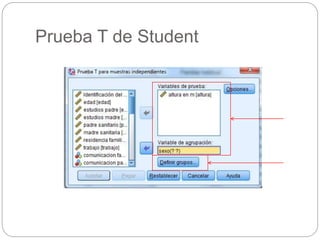
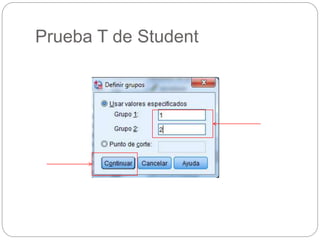
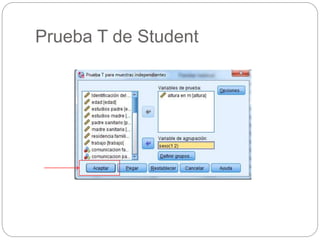
Este documento presenta un seminario sobre la prueba T de Student. Se analizan dos variables, escala y altura, en relación al sexo. Para escala, se encuentra que no hay relación con el sexo, por lo que chicos y chicas tienen la misma puntuación media. Para altura, se encuentra que sí hay relación con el sexo, concluyendo que los chicos son más altos que las chicas en promedio. El análisis incluye pruebas de normalidad y elección de la prueba T de Student para comparar las medias entre los grupos.

1. Seminario 8 Estadística
Cristina Téllez López,
Grupo 19, Grado en Enfermería, U.D. Virgen
del Rocío
Prueba T de Student

2. Ejercicio para el blog
 Observa la base de datos proporcionada:
estadistica_tic.sav
 Responder a las cuestiones:
 ¿Chicos y chicas tienen la misma puntuación media en las
escalas?
 ¿Chicos y chicas tiene la misma altura media?
 Comprueba antes de elegir el test la normalidad
mediante test estadístico y representación gráfica
y observa si se trata de muestras apareadas o
independientes.

3. 1ª actividad:
Prueba de normalidad en SPSS
 Sabiendo que la variable escala es cuantitativa y
la variable sexo es una cualitativa dicotómica,
solo haremos la prueba de normalidad a la
cuantitativa.
 Establecemos 2 hipótesis:
 H0: La variable se distribuye normalmente
 H1: La variable no se distribuye normalmente

4. Prueba de normalidad en SPSS

5. Prueba de normalidad en SPSS

6. Prueba de normalidad en SPSS

7. Prueba de normalidad en SPSS

8. Prueba de normalidad en SPSS
 Como la significación es 0,231>0,05, el resultado
no se considera significativo, por lo que
tendríamos que aceptar la H0, la variable
cumplen con la normalidad.

9. Prueba de normalidad en SPSS
(gráficamente)
 Podemos observar gráficamente que la variable
se distribuye normalmente

10. Elección de la prueba
 Por lo tanto: una variable cualitativa dicotómica y
otra cuantitativa con distribución normal, y son
independientes (diferentes muestras). Para
decidir una prueba que utilizar:

11. Establecemos las hipótesis
 Una vez decidida ya la prueba que vamos a
realizar, vamos a establecer las hipótesis.
 ¿Chicos y chicas tienen la misma puntuación media
en las escalas?
 H0: No hay relación entre el sexo y la escala.
 H1: Hay relación entre sexo y escala.
 Nivel de confianza: 95%

12. Prueba T de Student

13. Prueba T de Student
1
2

14. Prueba T de Student

15. Prueba T de Student

16. Prueba T de Student
 Como la significación es 0,423>0,05, la variable
no es representativa.
 Se acepta la H0, y se afirma que no existe
relación entre sexo y escala.

17. Conclusión 1ª actividad:
 ¿Chicos y chicas tienen la misma puntuación media
en las escalas?
 Sí, al no haber relación ente sexo y escala, ambos
grupos han obtenido puntuaciones similares.

18. 2ª actividad:
Prueba de normalidad
 Sabiendo que la variable altura es cuantitativa y
la variable sexo es una cualitativa dicotómica,
solo haremos la prueba de normalidad a la
cuantitativa.
 Establecemos 2 hipótesis:
 H0: La variable se distribuye normalmente
 H1: La variable no se distribuye normalmente

19. Prueba de normalidad

20. Prueba de normalidad
2
1

21. Prueba de normalidad

22. Prueba de normalidad

23. Prueba de normalidad
 Como la significación es 0,082>0,05, el resultado
no se considera significativo, por lo que
tendríamos que aceptar la H0, la variable
cumplen con la normalidad.

24. Prueba de normalidad en SPSS
(gráficamente)
 Podemos observar gráficamente que la variable
se distribuye normalmente

25. Elección de la prueba
 Por lo tanto: una variable cualitativa dicotómica y
otra cuantitativa con distribución normal, y son
independientes (diferentes muestras). Para
decidir una prueba que utilizar:

26. Establecemos las hipótesis
 ¿Chicos y chicas tiene la misma altura media?
 H0: No hay relación entre
 H1: Hay relación entre sexo y escala.
 Nivel de confianza: 95%

27. Prueba T de Student

28. Prueba T de Student

29. Prueba T de Student

30. Prueba T de Student

31. Prueba T de Student
 Como la significación es <0,05, el resultado se
considera significativo.
 Se rechaza la H0, y se afirma que existe
relación entre sexo y altura.

32. Prueba T de Student
 Fijándonos en esta tabla podemos ver la
diferencia que hay ente varones y mujeres.
 Los hombres miden de media 1,7731 y las
mujeres, 1,6444.

33. Conclusión 2ª actividad:
 ¿Chicos y chicas tiene la misma altura media?
 No, los chicos son más altos que las chicas.

34. FIN