Descargado 32 veces
Subido porIan Santillann
Punto de equilibrio
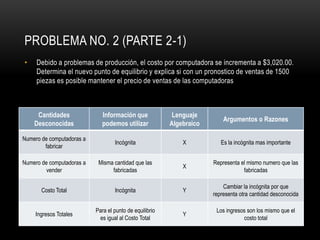
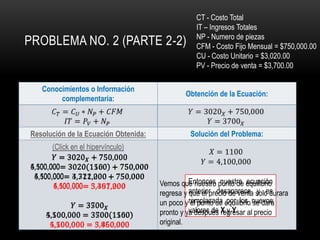
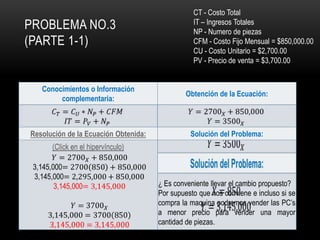
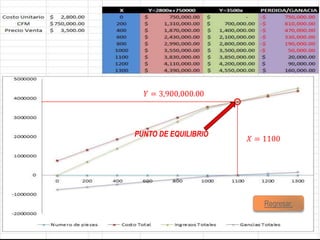
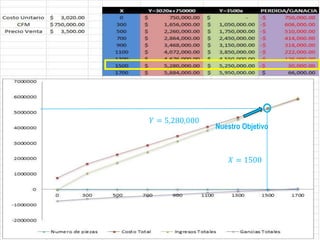
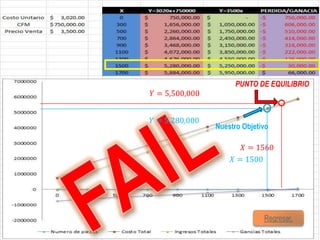
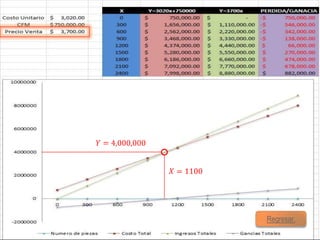
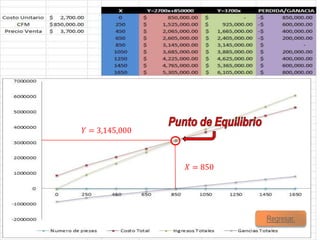
El documento presenta tres problemas relacionados con el cálculo del punto de equilibrio para una empresa fabricante de computadoras. En el primer problema, se calcula el punto de equilibrio cuando el costo de producción es de $2,800 por unidad y el precio de venta es de $3,500 por unidad, obteniendo aproximadamente 1,100 unidades. En el segundo problema, el costo aumenta a $3,020 por unidad, por lo que es necesario aumentar el precio de venta a $3,700 para mantener el punto de equilibrio. En el tercer problema, se
Más contenido relacionado
Similar a Punto de equilibrio
Punto de equilibrio
- 1. PUNTO DE EQUILIBRIO IANSANTILLAN GARCIA PROCESOS INDUSTRIALES UNIVERSIDAD TECNOLÓGICA DE TORREÓN
- 2. INTRODUCCIÓN Ecuación de DosIncógnitas. • Un sistema de dos ecuaciones con dos incógnitas es igual que la ecuación lineal, con la única diferencia que en este en lugar de encontrar solo una incógnita buscaremos dos incógnitas. Estas dos incógnitas se representan por las letras “X” y “Y” cada una con un valor diferente. Punto de equilibrio. • Es comúnmente utilizado por las empresas para determinar las ventas , regido por la formula que dice que el total de ventas debe ser igual al total de ingresos, es decir, el punto donde no existe ganancia pero tampoco existe una perdida. A continuación veremos un ejercicio donde se muestra de una mejor manera el sistema de dos incógnitas y el punto de equilibrio.
- 3. PROBLEMA NO. 1(PARTE 1-1) • La fabrica de computadoras HAL tiene costos fijos mensuales de $750,000.00. El costo de fabricación de cada computadora Notebook-9000 es de $2,800.00. El precio de venta de este modelo es de $3,500.00. Determina el punto de equilibrio. Es decir el numero de computadoras que deben fabricarse y venderse de tal modo que no haya perdidas ni ganancias. Cantidades Desconocidas Información que podemos utilizar Lenguaje Algebraico Argumentos o Razones Numero de computadoras a fabricar Incógnita X Es la incógnita mas importante Numero de computadoras a vender Misma cantidad que las fabricadas X Representa el mismo numero que las fabricadas Costo Total Incógnita Y Cambiar la incógnita por que representa otra cantidad desconocida Ingresos Totales Para el punto de equilibrio es igual al Costo Total Y Los ingresos son los mismo que el costo total
- 4. PROBLEMA NO. 1 (PARTE1-2) CT - Costo Total IT – Ingresos Totales NP - Numero de piezas CFM - Costo Fijo Mensual = $750,000.00 CU - Costo Unitario = $2,800.00 PV - Precio de venta = $3,500.00 Conocimientos o Información complementaria: Obtención de la Ecuación: Resolución de la Ecuación Obtenida: Solución del Problema: (Click en el hipervínculo) ERRORES ACEPTABLES Justificación: El punto de equilibrio se encuentra cerca de las 1100 unidades
- 5. PROBLEMA NO. 2(PARTE 2-1) • Debido a problemas de producción, el costo por computadora se incrementa a $3,020.00. Determina el nuevo punto de equilibrio y explica si con un pronostico de ventas de 1500 piezas es posible mantener el precio de ventas de las computadoras Cantidades Desconocidas Información que podemos utilizar Lenguaje Algebraico Argumentos o Razones Numero de computadoras a fabricar Incógnita X Es la incógnita mas importante Numero de computadoras a vender Misma cantidad que las fabricadas X Representa el mismo numero que las fabricadas Costo Total Incógnita Y Cambiar la incógnita por que representa otra cantidad desconocida Ingresos Totales Para el punto de equilibrio es igual al Costo Total Y Los ingresos son los mismo que el costo total
- 6. PROBLEMA NO. 2(PARTE 2-2) CT - Costo Total IT – Ingresos Totales NP - Numero de piezas CFM - Costo Fijo Mensual = $750,000.00 CU - Costo Unitario = $3,020.00 PV - Precio de venta = $3,500.00 Conocimientos o Información complementaria: Obtención de la Ecuación: Resolución de la Ecuación Obtenida: Solución del Problema: (Click en el hipervínculo) Nuestro objetivo era fabricar únicamente 1500 piezas y ver si podíamos mantener nuestro precio de venta, pero no se pudo alcanzar el punto de equilibrio, es necesario incrementar el precio del producto y para eso hacemos lo siguiente: Click aquí
- 7. PROBLEMA NO. 2(PARTE 2-2) CT - Costo Total IT – Ingresos Totales NP - Numero de piezas CFM - Costo Fijo Mensual = $750,000.00 CU - Costo Unitario = $3,020.00 PV - Precio de venta = $3,700.00 Conocimientos o Información complementaria: Obtención de la Ecuación: Resolución de la Ecuación Obtenida: Solución del Problema: (Click en el hipervínculo) Entonces nuestra ecuación Vemos que nuestro punto de equilibrio regresa y anterior desaparece solo durara que el precio de venta y es un poco yremplazada equilibrio nuevos el punto de por los se dará valores de regresar pronto y ya después X y Y. al precio original.
- 8. PROBLEMA NO.3 (PARTE1-1) • Uno de los componentes de la notebook.2012 se compra a un proveedor internacional. el jefe de ingeniería propone que si se deja de comprar dicho componente para fabricarlo dentro de la empresa, se aumenta el costo fijo de la notebook a $850,000. Pero se reduce el costo unitario de producción a $2700. si la demanda pronosticada sigue siendo de 1500 piezas mensuales ¿Es conveniente llevar el cambio propuesto? Cantidades Desconocidas Información que podemos utilizar Lenguaje Algebraico Argumentos o Razones Numero de computadoras a fabricar Incógnita X Es la incógnita mas importante Numero de computadoras a vender Misma cantidad que las fabricadas X Representa el mismo numero que las fabricadas Costo Total Incógnita Y Cambiar la incógnita por que representa otra cantidad desconocida Ingresos Totales Para el punto de equilibrio es igual al Costo Total Y Los ingresos son los mismo que el costo total
- 9. PROBLEMA NO.3 (PARTE 1-1) CT- Costo Total IT – Ingresos Totales NP - Numero de piezas CFM - Costo Fijo Mensual = $850,000.00 CU - Costo Unitario = $2,700.00 PV - Precio de venta = $3,700.00 Conocimientos o Información complementaria: Obtención de la Ecuación: Resolución de la Ecuación Obtenida: Solución del Problema: (Click en el hipervínculo) ¿ Es conveniente llevar el cambio propuesto? Por supuesto que nos conviene e incluso si se compra la maquina podremos vender las PC’s a menor precio para vender una mayor cantidad de piezas.
- 10.
- 11.
- 12.
- 13. PUNTO DE EQUILIBRIO NuestroObjetivo Regresar.
- 14.
- 15.