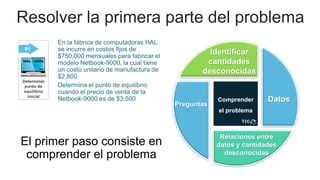
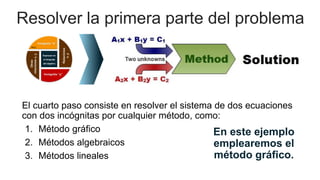
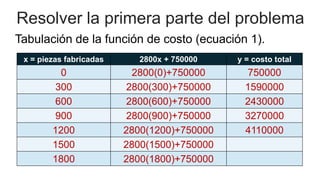
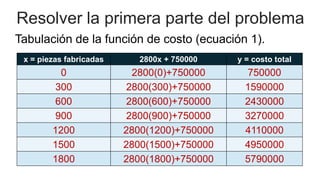
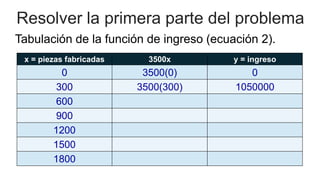
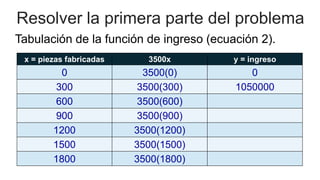
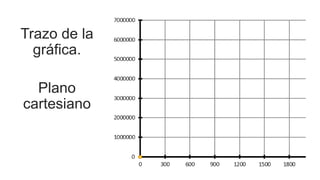
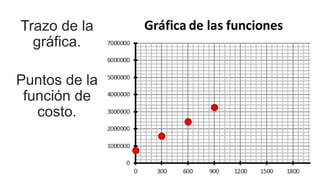
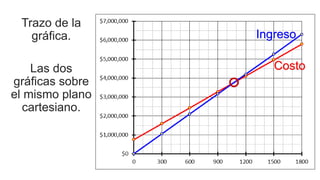
El documento aborda el uso de matemáticas en la toma de decisiones profesionales, enfocándose en la resolución de problemas de razonamiento mediante sistemas de ecuaciones lineales. Se presenta el concepto de punto de equilibrio, que es la cantidad de productos que deben venderse para cubrir costos y evitar pérdidas. Además, se incluye un ejemplo detallado sobre la producción y venta de un modelo de computadora, analizando diferentes escenarios financieros.

1. Break
Even
Point
G. Edgar Mata Ortiz

2. Mathematics
“In mathematics, the
art of proposing a
question must be
held of higher value
than solving it ”
George Cantor (1845 – 1918)

3. Contenido
Problemas de
razonamiento01 Sistemas de dos
ecuaciones lineales02
Punto de equilibrio03 Ejemplo (4 partes)04
Math Model

4. Problemas de razonamiento
Estos problemas muestran algunas de las aplicaciones
de la matemática a diferentes situaciones de la vida
real.

5. Problemas de razonamiento
En el presente documento se plantea un tema relacionado con
la vida profesional; el uso de la matemática para la elección de
un curso de acción o toma de decisiones.

6. Problemas de razonamiento
La solución de un problema de
razonamiento requiere de un
proceso de “modelado” o
representación de la situación
real en términos de variables y
relaciones matemáticas

7. Problemas de razonamiento

8. Sistemas de dos ecuaciones lineales
con dos incógnitas.Linear
equations
Los sistemas de ecuaciones lineales
son un resultado matemático y no
tienen un significado específico en el
mundo real.
Para que los objetos matemáticos sean
aplicados a la realidad es necesario
expresar la información en términos de
esta ciencia.

9. Sistemas de dos ecuaciones lineales
con dos incógnitas.Linear
equations
Con la finalidad de que el problema planteado pueda
resolverse mediante un sistema de dos ecuaciones
lineales es necesario establecer algunos postulados:
1. Las variables que describen el problema se
reducirán a dos para poder emplear sistemas de
2 ecuaciones con 2 incógnitas
2. Se asume que las relaciones entre variables son
lineales

10. Punto de equilibrio
Al resolver un problema de razonamiento es necesario
emplear conocimientos de la disciplina o ciencia a la
que pertenece el problema que se resolverá: Física,
economía, finanzas, química, termodinámica, entre
muchas otras.

11. Punto de equilibrio
El conocimiento necesario para resolver este problema es el
punto de equilibrio entre los costos en que se incurre para
producir un artículo, y los ingresos por su venta. Se le llama
punto de equilibrio a la cantidad de artículos que deben
producirse y venderse para que no haya pérdidas ni ganancias.

12. Punto de equilibrio
Los costos e ingresos dependen de la cantidad de
productos fabricados y vendidos, cada una de estas
variables se representará mediante una función lineal.

13. Ejemplo
Una buena forma de aprender es mediante ejemplos.
En las siguientes diapositivas se resuelve un problema de
razonamiento mostrando detalladamente cada paso del
proceso.
Modelo
Matemático

14. Ejemplo
Primera Parte
En la fábrica de computadoras HAL
se incurre en costos fijos de
$750,000 mensuales para fabricar el
modelo Netbook-9000, la cual tiene
un costo unitario de manufactura de
$2,800.
Determina el punto de equilibrio
cuando el precio de venta de la
Netbook-9000 es de $3,500

15. Ejemplo
Segunda Parte
Debido a problemas de operación, el
costo unitario de producción de la
Netbook-9000 se ha elevado a
$3,020, mientras el costo fijo
permanece constante.
Determina el nuevo punto de
equilibrio si no se desea alterar el
precio de venta.

16. Ejemplo
Tercera Parte
Si el costo fijo se mantiene
constante a pesar del aumento en el
costo unitario de producción, y el
pronóstico de ventas indica que se
venderán 1,600 piezas por mes, ¿es
conveniente, económicamente,
mantener el precio de venta?
Justifica tu respuesta.

17. Ejemplo
Cuarta Parte
Uno de los componentes de la
Netbook-9000 se compra a un
proveedor internacional. El jefe de
ingeniería propone que, si se deja
de comprar dicho componente para
fabricarlo dentro de la empresa, se
aumenta el costo fijo de la Netbook,
de $750,000 a $850,000 pero se
reduce el costo unitario de
producción, de $3,020 a $2,700.

18. Ejemplo
Cuarta Parte
Si la demanda pronosticada se
mantiene en 1,600 piezas
mensuales, ¿es conveniente llevar a
cabo el cambio propuesto? justifica
tu respuesta

19. Problemas de razonamiento

21. Problemas de razonamiento
En realidad se deben resolver cuatro problemas
independientes.

22. Cuatro problemas independientes
01 02 03 04
Determinar
punto de
equilibrio
inicial
Determinar
un segundo
punto de
equilibrio
Análisis del
precio de
venta
¿Es mejor
comprar o
fabricar?

23. Resolver la primera parte del problema
01
Determinar
punto de
equilibrio
inicial
En la fábrica de computadoras HAL
se incurre en costos fijos de
$750,000 mensuales para fabricar el
modelo Netbook-9000, la cual tiene
un costo unitario de manufactura de
$2,800.
Determina el punto de equilibrio
cuando el precio de venta de la
Netbook-9000 es de $3,500

24. Resolver la primera parte del problema
El primer paso consiste en
comprender el problema
Comprender
el problema
Identificar
cantidades
desconocidas
Datos
Relaciones entre
datos y cantidades
desconocidas
Preguntas

25. Resolver la primera parte del problema
Las cantidades desconocidas son:
1. Cantidad de computadoras que se van a fabricar y vender
2. Costo de fabricación de ese número de computadoras
3. Ingresos por las computadoras que se van a vender
Identificar
cantidades
desconocidas

26. Resolver la primera parte del problema
Los datos disponibles son:
1. Costo fijo = $750,000
2. Costo unitario de fabricación = $2,800
3. Precio de venta por pieza = $3,500
Datos

27. Resolver la primera parte del problema
Las relaciones que pueden establecerse son:
1. Costo total = Costo fijo + costo variable
2. Ingresos = precio de venta por número de piezas vendidas
3. Punto de equilibrio: Costo total = Ingresos
Relaciones entre
datos y cantidades
desconocidas

28. Resolver la primera parte del problema
Solamente nos preguntan una cosa:
¿Cuál es el punto de equilibrio?
Preguntas

29. Resumen del primer paso
Identificar las cantidades desconocidas
Datos disponibles
Relaciones entre cantidades desconocidas y datos
¿Qué es lo que nos preguntan?
Número de computadores que se van a fabricar y
vender, costo de fabricación e ingreso.
Costo fijo = $750,000 /mes , costo unitario = $2,800,
precio de venta = $3,500
Costo total = Costo fijo + Costo variable, Ingresos = Precio de venta
por número de piezas, Punto de equilibrio: Costo total = Ingreso
Punto de equilibrio: Cantidad de piezas a fabricar y
vender para que no haya pérdidas ni ganancias.

30. Resumen del primer paso
Este primer paso resulta muy largo de explicar debido a que estamos tratando de poner
por escrito lo que sucede en la mente de la persona que está analizando el problema.
Más adelante ordenaremos la información de tal forma que sea posible, para cualquier
persona, seguir la línea de razonamientos que condujo al planteamiento y resolución del
problema.

31. Organizador visual de la información
Número de
piezas que se
van a fabricar
Número de
piezas que se
van a vender

32. Organizador visual de la información
Número de
piezas que se
van a fabricar
Número de
piezas que se
van a vender
𝐶𝐹 = $750,000
𝐶𝑈 = $2,800
𝑃𝑉 = $3,500
El organizador
visual puede incluir
los datos, aunque
no es obligatorio

33. Resolver la primera parte del problema
El segundo paso consiste en
expresar algebraicamente las
cantidades desconocidas,
datos, y sus relaciones.
Expresar en
el lenguaje
del álgebra
Incógnita “x”
Relaciones
x,y
Incógnita “y”
Otras
relacionesx,y

34. Resolver la primera parte del problema
Naturalmente este segundo paso toma como base la
información generada en el primer paso: cantidades
desconocidas, datos y relaciones que serán expresadas
como ecuaciones lineales.

35. Resolver la primera parte del problema
Vamos a anotar esta segunda parte en una tabla con la
finalidad de que podamos comunicar mejor el proceso de
solución a otras personas.

36. Resolver la primera parte del problema
La tabla contendrá las
cantidades desconocidas,
sus interrelaciones, y su
expresión algebraica.
Cantidades
desconocidas
Información
disponible y/o
interrelaciones
Expresión
algebraica

37. Lenguaje algebraico
Cantidades
desconocidas
Información
disponible y/o
interrelaciones
Expresión
algebraica
Número de piezas
que se van a fabricar
Incógnita x
Cualquiera de las cantidades desconocidas puede tomarse como
incógnita, en este caso se ha decidido tomar la cantidad de
computadoras que van a fabricarse como incógnita e identificarla
con la letra equis.

38. Lenguaje algebraico
Cantidades
desconocidas
Información
disponible y/o
interrelaciones
Expresión
algebraica
Número de piezas
que se van a fabricar
Incógnita x
Número de piezas
que se van a vender
Se considera que se
venden todas las
piezas fabricadas
x
Este postulado de piezas vendidas igual a piezas fabricadas tiene
la finalidad de simplificar el modelo

39. Lenguaje algebraico
Cantidades
desconocidas
Información disponible
y/o interrelaciones
Expresión algebraica
Número de piezas que
se van a fabricar
Incógnita x
Número de piezas que
se van a vender
Se considera que se
venden todas las piezas
fabricadas
x
Costo total de
producción
Se considerará como
una segunda incógnita
y
Cuando se plantea un problema con dos incógnitas se busca
establecer las ecuaciones después de este paso.

40. Lenguaje algebraico
Cantidades
desconocidas
Información disponible
y/o interrelaciones
Expresión algebraica
Número de piezas que
se van a fabricar
Incógnita x
Número de piezas que
se van a vender
Se considera que se
venden todas las piezas
fabricadas
x
Costo total de
producción
Se considerará como
una segunda incógnita
y
Ingresos por ventas
En el punto de equilibrio,
los costos son iguales a
los ingresos
y

41. Resumen del segundo paso
Este segundo paso fue,
sencillamente, una
traducción del lenguaje
natural al algebraico.
TRADUCCIÓN
Lenguaje natural Lenguaje algebraico

42. Resolver la primera parte del problema
El tercer paso consiste en obtener
las ecuaciones que relacionan las
incógnitas y los datos.
𝒚 = 𝒇(𝒙)

43. Resolver la primera parte del problema
El tercer paso consiste en
obtener las ecuaciones que
relacionan las incógnitas y
los datos.
Para efectuar el tercer paso debemos recurrir a
información o conocimientos adicionales a los que el
problema presenta, en este caso, la forma de calcular los
costos totales y los ingresos.

44. El tercer paso consiste en obtener las dos ecuaciones
con dos incógnitas. Primera ecuación:
Costo total = Costo fijo + Costo variable
CT = CF + Costo unitario x Número de piezas
CT = CF + CU x NP
y = 750,000 + 2,800(x)
y = 2,800x + 750,000
Esta última expresión algebraica se identificará como ecuación 1.
Resolver la primera parte del problema

45. El tercer paso consiste en obtener las dos ecuaciones
con dos incógnitas. Segunda ecuación:
Ingreso = Precio de venta x Núm. de piezas
I = PV x NP
y = 3,500(x)
y = 3,500x
Esta última expresión algebraica se identificará como ecuación 2.
Resolver la primera parte del problema

46. Resumen del tercer paso
La obtención de las ecuaciones se basa en conocimientos previos, algún
dato del problema o una combinación de las dos cosas.
En este caso se utilizaron conocimientos acerca de costo total e ingreso y
algunos datos.
El resultado es un sistema de dos ecuaciones con dos incógnitas
Ecuación 1: y = 2,800x + 750,000
Ecuación 2: y = 3,500x
𝒚 = 𝒇(𝒙)

47. Resolver la primera parte del problema
El cuarto paso consiste en resolver el sistema de dos ecuaciones
con dos incógnitas por cualquier método, como:
1. Método gráfico
2. Métodos algebraicos
3. Métodos lineales

48. Resolver la primera parte del problema
El cuarto paso consiste en resolver el sistema de dos ecuaciones
con dos incógnitas por cualquier método, como:
1. Método gráfico
2. Métodos algebraicos
3. Métodos lineales
En este ejemplo
emplearemos el
método gráfico.

49. Resolver la primera parte del problema
El método gráfico requiere que se tabulen las dos
rectas y se grafiquen sobre el mismo plano para
localizar el punto de intersección, que es la solución.

50. Resolver la primera parte del problema
Tabulación de la función de costo (ecuación 1).
x = piezas fabricadas 2800x + 750000 y = costo total

51. Resolver la primera parte del problema
Tabulación de la función de costo (ecuación 1).
x = piezas fabricadas 2800x + 750000 y = costo total
0
300
600
900
1200
1500
1800

52. Resolver la primera parte del problema
Tabulación de la función de costo (ecuación 1).
x = piezas fabricadas 2800x + 750000 y = costo total
0 2800(0)+750000 750000
300 2800(300)+750000
600
900
1200
1500
1800

53. Resolver la primera parte del problema
Tabulación de la función de costo (ecuación 1).
x = piezas fabricadas 2800x + 750000 y = costo total
0 2800(0)+750000 750000
300 2800(300)+750000 1590000
600
900
1200
1500
1800

54. Resolver la primera parte del problema
Tabulación de la función de costo (ecuación 1).
x = piezas fabricadas 2800x + 750000 y = costo total
0 2800(0)+750000 750000
300 2800(300)+750000
600 2800(600)+750000
900 2800(900)+750000
1200 2800(1200)+750000
1500 2800(1500)+750000
1800 2800(1800)+750000

55. Resolver la primera parte del problema
Tabulación de la función de costo (ecuación 1).
x = piezas fabricadas 2800x + 750000 y = costo total
0 2800(0)+750000 750000
300 2800(300)+750000 1590000
600 2800(600)+750000 2430000
900 2800(900)+750000
1200 2800(1200)+750000
1500 2800(1500)+750000
1800 2800(1800)+750000

56. Resolver la primera parte del problema
Tabulación de la función de costo (ecuación 1).
x = piezas fabricadas 2800x + 750000 y = costo total
0 2800(0)+750000 750000
300 2800(300)+750000 1590000
600 2800(600)+750000 2430000
900 2800(900)+750000 3270000
1200 2800(1200)+750000 4110000
1500 2800(1500)+750000
1800 2800(1800)+750000

57. Resolver la primera parte del problema
Tabulación de la función de costo (ecuación 1).
x = piezas fabricadas 2800x + 750000 y = costo total
0 2800(0)+750000 750000
300 2800(300)+750000 1590000
600 2800(600)+750000 2430000
900 2800(900)+750000 3270000
1200 2800(1200)+750000 4110000
1500 2800(1500)+750000 4950000
1800 2800(1800)+750000 5790000

58. Resolver la primera parte del problema
Tabulación de la función de ingreso (ecuación 2).
x = piezas fabricadas 3500x y = ingreso

59. Resolver la primera parte del problema
Tabulación de la función de ingreso (ecuación 2).
x = piezas fabricadas 3500x y = ingreso
0
300
600
900
1200
1500
1800

60. Resolver la primera parte del problema
Tabulación de la función de ingreso (ecuación 2).
x = piezas fabricadas 3500x y = ingreso
0 3500(0) 0
300 3500(300)
600
900
1200
1500
1800

61. Resolver la primera parte del problema
Tabulación de la función de ingreso (ecuación 2).
x = piezas fabricadas 3500x y = ingreso
0 3500(0) 0
300 3500(300) 1050000
600
900
1200
1500
1800

62. Resolver la primera parte del problema
Tabulación de la función de ingreso (ecuación 2).
x = piezas fabricadas 3500x y = ingreso
0 3500(0) 0
300 3500(300) 1050000
600 3500(600)
900 3500(900)
1200 3500(1200)
1500 3500(1500)
1800 3500(1800)

63. Resolver la primera parte del problema
Tabulación de la función de ingreso (ecuación 2).
x = piezas fabricadas 3500x y = ingreso
0 3500(0) 0
300 3500(300) 1050000
600 3500(600) 2100000
900 3500(900) 3150000
1200 3500(1200)
1500 3500(1500)
1800 3500(1800)

64. Resolver la primera parte del problema
Tabulación de la función de ingreso (ecuación 2).
x = piezas fabricadas 3500x y = ingreso
0 3500(0) 0
300 3500(300) 1050000
600 3500(600) 2100000
900 3500(900) 3150000
1200 3500(1200) 4200000
1500 3500(1500) 5250000
1800 3500(1800)

65. Resolver la primera parte del problema
Tabulación de la función de ingreso (ecuación 2).
x = piezas fabricadas 3500x y = ingreso
0 3500(0) 0
300 3500(300) 1050000
600 3500(600) 2100000
900 3500(900) 3150000
1200 3500(1200) 4200000
1500 3500(1500) 5250000
1800 3500(1800) 6300000

66. Trazo de la
gráfica.
Plano
cartesiano

67. Trazo de la
gráfica.
Puntos de la
función de
costo.

68. Trazo de la
gráfica.
Puntos de la
función de
costo.

69. Trazo de la
gráfica.
Las dos
gráficas sobre
el mismo plano
cartesiano.
Ingreso
Costo

70. Trazo de la
gráfica.
Las dos
gráficas sobre
el mismo plano
cartesiano.
Ingreso
Costo

71. Trazo de la
gráfica.
Las dos
gráficas sobre
el mismo plano
cartesiano.
Ingreso
Costo

72. Trazo de la
gráfica.
Las dos
gráficas sobre
el mismo plano
cartesiano.
Ingreso
Costo

73. Trazo de la
gráfica.
Localización, a
simple vista,
de las
coordenadas
del punto de
intersección.
Ingreso
Costo

74. Trazo de la
gráfica.
Las
coordenadas
del punto de
intersección
son la
solución del
problema.
Ingreso
Costo

75. Comprobación
2,800 750,000
2,800( ) 750,000
2'996,000 750,000
3'74
3'800,000 1,070
3'800,000
3'800,000
3'800,000 1,070
3'800,000
6
3,500
3,500( )
3'745,000
,000
y
Error aceptable
Error aceptab
y x
x
le
= +
= +
= +
=
=
=
=
Esta es una de las limitaciones del método gráfico; no siempre es posible obtener el
resultado exacto, pero se considera aceptable si el error es menor a un 2% ó 3%.z
Ingreso
Costo

76. Paso 3. Ejecutar el plan: Resolver el sistema de ecuaciones, obtener los valores de las incógnitas.
Comprobación
2,800 750,000
2,800( ) 750,000
2'996,000 750,000
3'74
3'800,000 1,070
3'800,000
3'800,000
3'800,000 1,070
3'800,000
6
3,500
3,500( )
3'745,000
,000
y
Error aceptable
Error aceptab
y x
x
le
= +
= +
= +
=
=
=
=
La comprobación se escribe en la sección del formato que dice:
Paso 3. Ejecutar el plan: resolver el sistema de ecuaciones, obtener los valores de las incógnitas.
En el método gráfico el
resultado no siempre es
exacto, sin embargo, se
considera aceptable cuando el
error no es mayor al 3% del
valor deseado

77. Resumen del cuarto paso
Se resolvió el sistema de dos ecuaciones con dos incógnitas
por el método gráfico.
Se acepta un error entre el 2% y el 3% en la comprobación.
Los valores de “x, y” son la solución del problema.

78. Resumen del cuarto paso
El punto de equilibrio es:
x = 1,070 y = 3’800,000
Lo cuál significa que deben fabricarse y venderse 1,070 piezas
para que tanto el costo como el ingreso sean de 3’800,000 con
lo cuál no habrá pérdidas ni ganancias.

79. Información en el formato 3.3
Paso 4. Respuesta, revisión y comprobación: Escribir valores de todas las cantidades desconocidas y
verificar que se cumplen todas las condiciones del problema.
Número de piezas que se van a fabricar y vender: x = 1070
Costo variable: 2800x = 2800 (1070) = $2’996,000
Costo total: y = 750,000 + 2’996,000 = $3’746,000

80. Cuatro problemas independientes
01 02 03 04
Determinar
punto de
equilibrio
inicial
Determinar
un segundo
punto de
equilibrio
Análisis del
precio de
venta
¿Es mejor
comprar o
fabricar?

81. Cuatro problemas independientes
Solamente se ha resuelto la primera parte del problema, las cuatro
partes serán revisadas en el formato 3.3 la próxima clase.

82. Gracias
Por su atención
licmata@hotmail.com
http://licmata-math.blogspot.com/
http://www.slideshare.net/licmata/
http://www.facebook.com/licemata
Twitter: @licemata