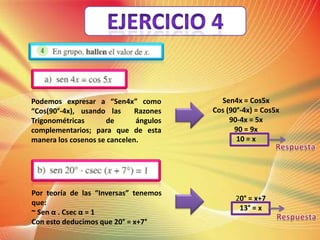
Este documento presenta los pasos de resolución de dos problemas trigonométricos. En el primer problema, se expresa "Sen4x" como "Cos5x" usando las razones trigonométricas de ángulos complementarios. Luego, aplicando teorías de inversas, se deduce que la solución es x=10°. En el segundo problema, se expresa "tg3x" como "Cot6x" siguiendo un proceso similar, deduciendo así que la solución es también x=10°.

1. Integrantes
Rocio Milagros Callata Enriquez
Reina Aidita Bocanegra Ramirez
Profesor
Valentín Contreras
Grado y sección
5to “D”

2. Podemos expresar a “Sen4x” como
“Cos(90°-4x), usando las
Razones
Trigonométricas
de
ángulos
complementarios; para que de esta
manera los cosenos se cancelen.
Por teoría de las “Inversas” tenemos
que:
~ Sen α . Csec α = 1
Con esto deducimos que 20° = x+7°
Sen4x = Cos5x
Cos (90°-4x) = Cos5x
90-4x = 5x
90 = 9x
10 = x
20° = x+7
13° = x

3. Por teoría de las “Inversas” tenemos
que:
~ Cos α . Sec α = 1
Con esto deducimos que 38° = x+8°
Podemos expresar a “tg3x” como
“Cot(90°-3x), usando las
Razones
Trigonométricas
de
ángulos
complementarios; para que de esta
manera las cotangentes se cancelen.
38° = x+8
30° = x
tg3x = Ctg6x
Cot (90°-3x) = Ctg6x
90-3x = 6x
90 = 9x
10 = x