Este documento presenta identidades trigonométricas para la suma y el producto de senos y cosenos. Incluye demostraciones de identidades como senA + senB = 2sen(A/2)cos(B/2) y 2senxcose = sen(x + y) + sen(x - y). También cubre aplicaciones numéricas de estas identidades y series trigonométricas para sumas de senos y cosenos con ángulos en progresión aritmética.

1. 1
UNIVERSIDAD NACIONAL DEL SANTA
CEPUNS
Ciclo 2015-III
TRIGONOMETRÍA
“TRANSFORMACIONES TRIGONOMÉTRICAS ’’
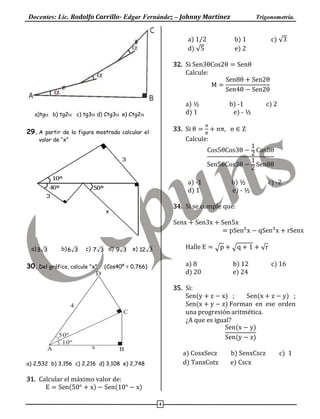
Docentes: Lic. Rodolfo Carrillo- Edgar Fernández – Johnny Martínez
IDENTIDADES PARA AL SUMA Y
PRODUCTO DE SENOS Y/O COSENOS.
Caso I:
Para la suma o diferencia de dos senos o
cosenos a producto.
SenA + SenB = 2Sen (
A + B
2
) Cos (
A − B
2
)
SenA − SenB = 2Cos (
A + B
2
) Sen (
A − B
2
)
CosA + CosB = 2Cos (
A + B
2
) Cos (
A − B
2
)
CosA − CosB = −2Sen (
A + B
2
) Sen (
A − B
2
)
Demostración:
Conocemos:
{
Sen(x + y) = SenxCosy + CosxSeny
Sen(x − y) = SenxCosy − CosxSeny
Cos(x + y) = CosxCosy − SenxSeny
Cos(x − y) = CosxCosy + SenxSeny
Si sumamos (1) + (2) obtenemos:
Sen(x + y) + Sen(x − y) = 2SenxCosy (∗)
Hacemos un cambio de variable:
Sea
x + y = A
x − y = B
}
Obtenemos:
x =
A + B
2
∧ y =
A − B
2
Luego de (∗):
SenA + SenB = 2Sen (
A + B
2
) Cos (
A − B
2
)
Las restantes identidades pueden
verificarse en forma analoga.
APLICACIÓN 1
1. Simplificar la expresión:
E =
Cos2x + Cos4x + Cos6x
Sen2x + Sen4x + Sen6x
a) Cosx b) Tanx c) -1
d) Cot4x e) Sen6x
2. Calcular el valor de:
E = [Sen38° + Sen22°]Sec8°
a) 1 b) 1/2 c) -1
d) 2 e) 0
3. Simplificar la expresión:
E =
Sen(3x + y) + Sen(x + 3y)
Sen2x + Sen2y
. Sec(x + y)
a) 3 b) 2 c) 4
d) 1 e) 0
4. Simplificar la siguiente expresión:
Sen10°
Cos20°
+
Cos40°
Sen70°
a) -1 b) 1 c) -2
d) ½ e) - ½
Caso II:
Para el producto de dos términos, Senos
y/o Cosenos a suma o diferencia.
Siendo x > y.
2SenxCosy = Sen(x + y) + Sen(x − y)
2SenyCosx = Sen(x + y) − Sen(x − y)
2CosxCosy = Cos(x + y) + Cos(x − y)
−2SenxSeny = Cos(x + y) − Cos(x − y)
APLICACIÓN 2
5. Simplificar la expresión:
Semana Nº 11

2. Docentes: Lic. Rodolfo Carrillo- Edgar Fernández – Johnny Martínez Trigonometría.
2
E = Sen6x. Sen4x − Sen15x. Sen13x
+ Sen19x. Sen9x
a) 0 b) -1 c) -2
d) 1 e) 0
6. Simplificar la expresión:
E =
Sen50° − 2Cos40°. Sen10°
Cos80° + 2Sen70°. Sen10°
a) -1 b) 0 c) 1
d) ½ e) -2
NOTA:
Sen2
x − Sen2
y = Sen(x + y). Sen(x − y)
Cos2
x − Sen2
y = Cos(x + y). Cos(x − y)
APLICACIÓN 3
7. Simplificar la expresion:
E = Cos(A + B). Cos(A − B) + Sen2
A
a) Cos2
B b) -1 c) Sen2
B
d) 1 e) 0
SUMA DE SERIES TRIGONOMÉTRICAS
Para la suma de Senos o Cosenos cuyos
ángulos están en progresión aritmética.
∑ Sen(x + (k − 1)r) =
Sen (
nr
2
)
Sen (
r
2
)
. Sen (
P + U
2
)
n
k=1
∑ Cos(x + (k − 1)r) =
Sen (
nr
2
)
Sen (
r
2
)
. Cos (
P + U
2
)
n
k=1
n=# de términos.
r= razón de P.A
P=primer ángulo
U=último ángulo
PROBLEMAS PROPUESTOS
CEPUNS 2010 II - TECER EXAMEN SUMATIVO
8. La expresion:
Senα + Sen3α
Sen2α + Sen4α
es equivalente a:
a) Cos2α/Sen3α b) Sen2α/Sen3α
c) Sen4α/Sen6α d) 1
e) Sen6α/Sen4α
9. Si Sen64° = k
¿A que es igual?
E = Cos2
43° − Sen2
17°
a)k/2 b) 2k c) 4k
d)k/4 e) 3k
10. Simplificar:
E = 2(Cos5x + Cos3x)(Sen3x − Senx)
a) Sen16x b) Sen8x c) Sen4x
d) 2Sen16x e) 2sen8x
11. Simplificar:
Sen7x − Sen5x
Cos7x + Cos5x
+
Sen3x − Senx
Cosx − Cos3x
a) Csc2x b) Sec2x c) Csc3x
d) Sec3x e) Cscx
12. Si 𝑥 = 20°; Calcular:
Sen2x + Sen3x + Sen4x
Cos2x + Cos3x + Cos4x
a) 1 b) ½ c) √3
d) 2 e) -1
13. Halle el valor de Q en la siguiente
ecuación:
QSen70° − Sen80° − Cos50° = 0
a) 2√2 b) √3 c) -2
d) 2 e) 0
TERCER EXAMEN SUMATIVO
14. Si: 𝑥 =
𝜋
13
𝑟𝑎𝑑 , entonces el valor de la
expresión: 𝐸 =
𝐶𝑜𝑠𝑥.𝐶𝑜𝑠10𝑥
𝐶𝑜𝑠2𝑥+𝐶𝑜𝑠4𝑥
, es:
a) - ½ b) ½ c) 1
d) – 3/2 e) - 1
TERCER EXAMEN SUMATIVO
15. En un triángulo ABC, se cumple que:
𝑆𝑒𝑛𝐴 = 𝑛. 𝑆𝑒𝑛𝐵. 𝑆𝑒𝑛𝐶
Cos𝐴 = 𝑛. 𝐶𝑜𝑠𝐵. 𝐶𝑜𝑠𝐶
Entonces el valor de TgA, es:
A) n-2 B) n-1 C) n

3. Docentes: Lic. Rodolfo Carrillo- Edgar Fernández – Johnny Martínez Trigonometría.
3
D) n+1 E) n+2
TERCER EXAMEN SUMATIVO
16. Al reducir la expresión se obtiene:
𝑅 =
𝐶𝑜𝑠10°−𝐶𝑜𝑠70°
𝑆𝑒𝑛40°+𝑆𝑒𝑛20°
a)


20
10
Sen
Cos b)


40
20
Cos
Sen c)


10
40
Cos
Sen
d)


20
40
Cos
Sen e) N.A.
TERCER EXAMEN SUMATIVO
17. Al simplificar:
𝑆𝑒𝑛(45°+𝑥)−𝑆𝑒𝑛(45°−𝑥)
𝐶𝑜𝑠(45°+𝑥)+𝐶𝑜𝑠(45°−𝑥)
A)
1
2
𝑆𝑒𝑛𝑥 b) 𝑇𝑔𝑥 c) 2√2𝐶𝑡𝑔𝑥
d) −
√2
2
𝐶𝑜𝑠𝑥 e) 2𝐶𝑜𝑠𝑥
18. Si: α + β = 60° y α − β = 45°
Calcular: E = Sen2
α − Sen2
β
a)√6/8 b) √6/6 c) √6/3
d)√6/4 e) √6/2
19. Si la siguiente igualdad es una
identidad, halla el valor de “A”
Sen2x + nSen3x + Sen4x
Cos2x + nCos3x + Cos4x
= 𝐀. Tan3x
a) n b) 1 c) 2n
d) 2 e) 3
20. En que triangulo ABC se cumple que:
Sen2B + Sen2C = Sen2A
a) Acutángulo b) rectángulo
c) No existe d) Obtusángulo
e) Faltan datos
21. ¿En que triangulo ABC, se cumple?
SenA =
SenB + SenC
CosB + CosC
a) Equilátero b) Isósceles
c) Rectángulo d) Obtusángulo
e) Acutángulo
22. Simplificar:
E =
Cos1 + Cos3 + Cos5 + Cos9
(Tan1 + cot1)(Sen11 + Sen5)
a) ¼ b) ½ c) 1
d) 2 e) 4
23. Simplificar:
E =
Senθ + SenSenkθ + Sen(2k − 1)θ
Cosθ + Coskθ + Cos(2k − 1)θ
a) Tankθ b) Tanθ c) Cotkθ
d) Cotθ e) 1
24. Si: 90° < 𝑥 < 180°.
Reducir:
S = √Senx(Sen3x + Senx)
a)Sen2x b) 2Cosx c) –Sen2x
d) -1 e) 1
CEPUNS 2009 III -TERCER EXAMEN SUMATIVO
25. Al reducir:
K =
SenxSen2x + Sen2xSen5x + Sen3xSen10x
CosxSen2x + Sen2xCos5x − Cos3xSen10x
n∈ 𝑁; se obtiene:
a) Cot7x b) Tan7x c) –Tan7x
d) –Cot7x e) Cos7x
26. Calcule el equivalente de la siguiente
expresión
2Cos(α + β)Cos(α + 2β) − Cosβ
Cos(2α + 3β)
+ Tan2
β
a) Csc2
β b) Sec2
β c) Sec2
α
d) Csc2
α e) −Tan2
β
27. Simplificar:
E =
Cos(a − 3b) − Cos(3a − b)
Sen2a + Sen2b
a) 2Sen(a + b) b) 2Cos(a + b)
c) 2Sen(a − b) d) 2Cos(a − b)
e) 2
28.Del gráfico , Calcular
AB
BC
T 

4. Docentes: Lic. Rodolfo Carrillo- Edgar Fernández – Johnny Martínez Trigonometría.
4
a)tgb) tg2 c) tg3 d) Ctg3e) Ctg2
29.A partir de la figura mostrada calcular el
valor de “x”
a) 33 b) 36 c) 37 d) 39 e) 312
30.Del gráfico, calcule "x" (Cos40º = 0,766)
a) 2,532 b) 3,156 c) 2,216 d) 3,108 e) 2,748
31. Calcular el máximo valor de:
E = Sen(50° + x) − Sen(10° − x)
a) 1/2 b) 1 c) √3
d) √5 e) 2
32. Si Sen3θCos2θ = Senθ
Calcule:
M =
Sen8θ + Sen2θ
Sen4θ − Sen2θ
a) ½ b) -1 c) 2
d) 1 e) - ½
33. Si θ =
π
8
+ nπ, n ∈ Z
Calcule:
Cos5θCos3θ −
1
2
Cos8θ
Sen5θCos3θ −
1
2
Sen8θ
a) -1 b) ½ c) -2
d) 1 e) - ½
34. Si se cumple que:
Senx + Sen3x + Sen5x
= pSen5
x − qSen3
x + rSenx
Halle E = √p + √q + 1 + √r
a) 8 b) 12 c) 16
d) 20 e) 24
35. Si:
Sen(y + z − x) ; Sen(x + z − y) ;
Sen(x + y − z) Forman en ese orden
una progresión aritmética.
¿A que es igual?
Sen(x − y)
Sen(y − z)
a) CosxSecz b) SenxCscz c) 1
d) TanxCotz e) Cscx
50º
10º
A B
C
D
4
x