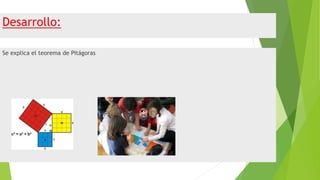
El documento describe una situación de aprendizaje basada en la didáctica crítica para enseñar el teorema de Pitágoras a estudiantes de educación media superior. La lección se divide en tres partes: apertura, desarrollo y cierre. En la apertura, los estudiantes exploran el teorema para resolver un problema sobre la longitud de una cuerda de puente. En el desarrollo, practican aplicando el teorema a ejemplos contextuales. En el cierre, realizan más ejercicios y reflexionan sobre su

1. Introducción:Introducción:
En la actualidad el proceso de enseñanza-aprendizaje encuentra en la didáctica crítica una
metodología en la cual el profesor ya no sea el dueño del conocimiento si no más bien, un
acompañante dentro del mismo proceso, por ello es importante que se genere la participación del
alumno para que de esta manera sea quien genere su propio aprendizaje en base a la reflexión y
problematización del mismo.
En éste caso se presenta el “teorema de Pitágoras en educación media superior” situación de
aprendizaje basado en los tres principales puntos de la didáctica critica.

2. Situación de aprendizaje con base a los planteamientos de la
didáctica critica.
Tres momentos metódicos, empleados para organizar situaciones de aprendizaje:
Apertura:
Primera
aproximación al
objeto
Desarrollo:
Elaboración del
conocimiento
Cierre:
reconstrucción del
fenómeno, nueva
síntesis

3. Situación de aprendizaje con base a los
planteamientos de la didáctica critica
Teorema de Pitágoras
Educación Media Superior

4. Necesito calcular la longitud de cuerda.
¿Qué puedo hacer?

5. Objetivos:
El alumno aprenderá a calcular los lados del triángulo mediante el teorema de Pitágoras
para solucionar situaciones reales, hipotéticas o formales.
Aprendizajes esperados:
 Identificar los lados del triángulo.
 Aplicar las formulas correspondientes para el calculo del lado del triángulo.
 Desarrollar habilidades matemáticas para interpretar y resolver situaciones reales, hipotéticas o
formales.

6. Escenario didáctico:
 Salón de clases
 Fuera del aula
 Pirámides de Teotihuacán, puentes, edificios, árboles, etc.
Materiales:
 Cuaderno, lápiz, goma
 Cinta métrica y gis blanco
Organización:
 Individual (trabajo en salón de clases)
 Grupal (en campo)

7. Didáctica:
 Identifica los catetos y la hipotenusa.
 Realiza operaciones aritméticas.
 Comprueba resultados.
 Crea situaciones similares aplicando el teorema de Pitágoras.

8. Didáctica.
Primera parte:
La actividad se llevara acabo en dos secciones, dentro del aula de clases donde primero se verá con
los alumnos la existencia de un problema: “la longitud de cuerda de un puente”. Después se
invitara al alumnado a investigar el teorema de Pitágoras y al azar expondrá un alumno.
Posteriormente se realizaran ejercicios contextuales e hipotéticos.

9. Didáctica.
Segunda parte:
Se llevara acabo en el exterior del salón, calculando alturas de arboles, salones. Generando
conocimiento de campo, para ello el alumno visitara diferentes lugares para calcular alturas o
distancias de postes, edificios, etc.

10. Desarrollo:
Se explica el teorema de Pitágoras

11. Ejemplo.- calcula el valor de “x” dado el siguiente triangulo aplicando el teorema de
Pitágoras

12. Teorema de Pitágoras
En un triangulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los
catetos
De esta formula se obtiene lo siguiente

13. Cierre
Aplicación del teorema de Pitágoras

14. Realización de ejercicios contextuales
 ¿Cuál es la longitud de la escalera que necesitan los bomberos para llegar a la habitación donde
esta el incendio?
 Calcula el ancho de la cancha de futbol.

15. Evaluación.
 ¿Qué aprendieron los alumnos?
 ¿Cuál es el comportamiento que presentaron al tener dificultad para interpretar situaciones
contextuales?
 ¿Fue significativo para cada uno de los alumnos?

16. Reflexión final
La Didáctica Critica busca la construcción del conocimiento en base a la interacción del alumno con
su entorno, por ello en ésta actividad se busca que el alumno sea quien investigue el tema y lo
exponga, rompiendo con la dependencia existente entre maestro-alumno.
Siendo el profesor un guía durante el proceso, la presentación también busca el trabajo individual
como en colectivo, permitiendo al alumno interactuar con sus compañeros interpretando y
reconstruyendo el conocimiento a partir de la reflexión y la problemática real presentada

17. Referencias:
 Construcción de conocimientos. Recuperado de http://etac.clientes.tralcom.com/tc-
etac/cursos/MODELOS_DISENO_C/U4/S4_02.html
 ELABORACIÓN DE PROGRAMAS de Margarita Pansza González. Recuperado de
http://infocuib.laborales.unam.mx/~ec10s02b/archivos/data/40/4.pdf
 Evaluación. Recuperado de http://etac.clientes.tralcom.com/tc-
etac/cursos/MODELOS_DISENO_C/U4/S4_06.html
 INSTRUMENTACIÓN DIDÁCTICA. De Margarita Pansza, Porfirio Morán 0., E.C. Pérez.
Recuperado de http://depa.fquim.unam.mx/dsa/PAIDOS/A10-Instrumentacion_Didactica.pdf
 Programa, propuesta de aprendizaje. Recuperado de http://etac.clientes.tralcom.com/tc-
etac/cursos/MODELOS_DISENO_C/U4/S4_04.html
 Realidad institucional y curricular. Recuperado de http://etac.clientes.tralcom.com/tc-
etac/cursos/MODELOS_DISENO_C/U4/S4_01.html?id_examen_act=1&id_inscripcion=33688
3
 Relación maestro-alumno. Recuperado de http://etac.clientes.tralcom.com/tc-
etac/cursos/MODELOS_DISENO_C/U4/S4_03.html
 Situaciones de aprendizaje. Recuperado de http://etac.clientes.tralcom.com/tc-
etac/cursos/MODELOS_DISENO_C/U4/S4_05.html