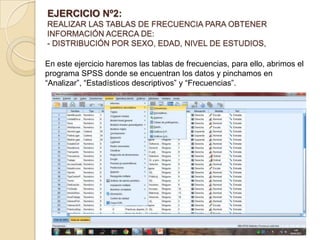
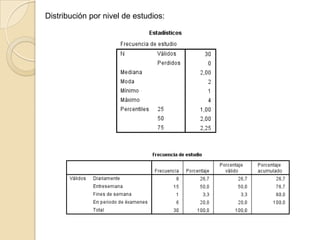
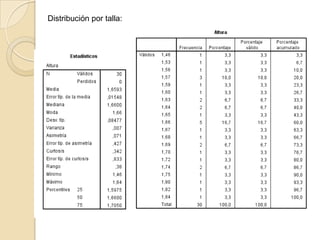
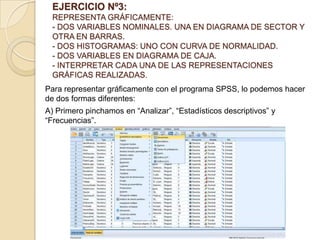
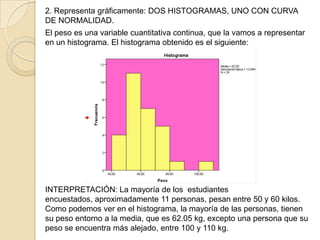
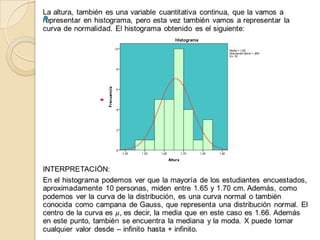
Este documento describe cómo realizar tablas de frecuencias, representaciones gráficas y tablas de contingencia en el programa estadístico SPSS. Incluye tres ejercicios: 1) crear tablas de contingencia para analizar las relaciones entre variables cualitativas, 2) crear tablas de frecuencias para variables cualitativas y cuantitativas, y 3) representar gráficamente variables mediante diagramas de sectores, barras, histogramas y diagramas de cajas e interpretar los resultados.

1. SEMINARIO Nº 5: REALIZAR TABLAS DE
FRECUENCIAS, REPRESENTACIONES
GRÁFICAS Y TABLAS DE CONTINGENCIA
EN EL PROGRAMA ESTADÍSTICO SPSS.
Vanesa Díaz Pérez.
Grupo 5.

2. EJERCICIO Nº1:
Realizar las tablas de contingencia para obtener información acerca de:
-¿Existe relación entre el tipo de centro educativo que proviene el
alumnado y la opción de elegir enfermería como primera opción?
-¿Existe relación entre elegir enfermería como primera opción y el sexo del
alumnado?
-¿Existe relación entre el gasto de móvil mensual y el sexo?
Para realizar las tareas de este seminario utilizaremos los datos que se
encuentran en la matriz en una encuesta a estudiantes.
Primero seleccionamos “Analizar”, “Estadísticos descriptivos” y “Tablas de
contingencia”.

3. Ahora elegimos las variables que irán en la fila y columna de la tabla de
contingencia. Después pincharemos en “Aceptar” para obtener la tabla de
contingencia.
En el primer apartado: ¿Existe relación entre el tipo de centro educativo que
proviene el alumnado y la opción de elegir enfermería como primera
opción? La tabla de contingencia obtenida es la siguiente:
Como podemos ver en la tabla de contingencia, la mayoría de las personas,
concretamente 15, eligieron como primera opción enfermería y pertenecían
a un colegio público.

4. En el segundo apartado:¿Existe relación entre elegir enfermería como
primera opción y el sexo del alumnado? La tabla de contingencia obtenida
es la siguiente:
Como podemos observar, la mayoría de las personas que eligió
enfermería como primera opción eran mujeres, concretamente 16 de los
30 estudiantes encuestados (Muestra).

5. En el tercer apartado:¿Existe relación entre el gasto de móvil mensual y el
sexo? Hemos obtenido la siguiente tabla de contingencia:
Como podemos ver, de los 30 estudiantes encuestados, la mayoría de las
mujeres (10) gastan menos de 15 euros al mes y solo un varón gasta esta
cantidad. El resto de varones (3) consume entre 15-25 euros y el resto de
las mujeres (15) consumen entre 15 a más de 45 euros. Una de las
personas no utilizará móvil, ya que se cuenta como un valor perdido.

6. EJERCICIO Nº2:
REALIZAR LAS TABLAS DE FRECUENCIA PARA OBTENER
INFORMACIÓN ACERCA DE:
- DISTRIBUCIÓN POR SEXO, EDAD, NIVEL DE ESTUDIOS,
En este ejercicio haremos las tablas de frecuencias, para ello, abrimos el
programa SPSS donde se encuentran los datos y pinchamos en
“Analizar”, “Estadísticos descriptivos” y “Frecuencias”.

7. Primero arrastramos una variable y después pinchamos en “Estadísticos”
y dependiendo si la variable es cualitativa (Nominal u ordinal) o
cuantitativa (Continua o discreta), marcaremos calcular unos parámetros
estadísticos u otros.

8. Empezamos con la variable sexo, que es una variable cualitativa nominal:

9. Distribución por edad:

10. Distribución por nivel de estudios:

11. Distribución por talla:

12. Distribución por trabajo:

13. EJERCICIO Nº3:
REPRESENTA GRÁFICAMENTE:
- DOS VARIABLES NOMINALES. UNA EN DIAGRAMA DE SECTOR Y
OTRA EN BARRAS.
- DOS HISTOGRAMAS: UNO CON CURVA DE NORMALIDAD.
- DOS VARIABLES EN DIAGRAMA DE CAJA.
- INTERPRETAR CADA UNA DE LAS REPRESENTACIONES
GRÁFICAS REALIZADAS.
Para representar gráficamente con el programa SPSS, lo podemos hacer
de dos formas diferentes:
A) Primero pinchamos en “Analizar”, “Estadísticos descriptivos” y
“Frecuencias”.

14. Ahora elegimos la variable y pinchamos en “Gráficos” y a continuación
podremos elegir la representación gráfica que queramos teniendo en
cuenta el tipo de variable. Por último pinchamos en “Aceptar” para
obtener el gráfico.

15. B) También podemos pinchar en “Gráficos” y “Generador de gráficos”.
Pinchamos en “Aceptar”.

16. A continuación, elegimos el gráfico y las variables que queremos
representar en él. Por último pinchamos en “Aceptar” para obtener el
gráfico.

17. Según lo explicado anteriormente, vamos a realizar los gráficos que se nos
piden en el ejercicio, utilizando una de las dos formas explicadas.
1. Representar gráficamente: DOS VARIABLES NOMINALES. UNA EN
DIAGRAMA DE SECTOR Y OTRA EN BARRAS E INTERPRETAR LOS
RESULTADOS.
La variable nominal sexo, la vamos a representar en diagrama de barras.
El diagrama de barras obtenido es el siguiente:
INTERPRETACIÓN:
Como podemos ver en el
diagrama de barras, en esta
encuesta a estudiantes, hay un
mayor número de mujeres que de
hombres, aproximadamente 26
mujeres y 4 hombres.

18. La variable nominal estado civil, la vamos a representar en diagrama de
sectores. El diagrama de sectores obtenido es el siguiente:
INTERPRETACIÓN:
Como podemos observar a simple vista, la mayoría de los estudiantes
encuestados son solteros/as (Color azul) y una pequeña parte son
separados/as o divorciados/as (Color verde).

19. 2. Representa gráficamente: DOS HISTOGRAMAS, UNO CON CURVA
DE NORMALIDAD.
El peso es una variable cuantitativa continua, que la vamos a representar
en un histograma. El histograma obtenido es el siguiente:
INTERPRETACIÓN: La mayoría de los estudiantes
encuestados, aproximadamente 11 personas, pesan entre 50 y 60 kilos.
Como podemos ver en el histograma, la mayoría de las personas, tienen
su peso entorno a la media, que es 62.05 kg, excepto una persona que su
peso se encuentra más alejado, entre 100 y 110 kg.

20. 

21. 3. Representa gráficamente: DOS VARIABLES EN DIAGRAMA DE
CAJAS.
En el diagrama de cajas o bigotes, hemos elegido la variable peso
(Variable cuantitativa continua) y la variable sexo (Variable cualitativa
nominal). El diagrama de cajas o bigotes obtenido es el siguiente:

22. INTERPRETACIÓN:
En este diagrama podemos ver que la mediana o P50 O 2º cuartil, es
aproximadamente 81en los varones y 58 en las mujeres.
El P25 o 1º cuartil, en los varones es aproximadamente 75 y en las
mujeres aproximadamente 53.
El P75 o 3º cuartil, en los varones es aproximadamente 94 y en las
mujeres 62.
El P97 o extremo del “Bigote” de comienzo de los valores atípicos del
exceso, en los varones es aproximadamente 100 y en las mujeres es
aproximadamente 77.
El P3 o extremo del “Bigote” de comienzo de los valores atípicos por
defecto, es aproximadamente 42 en las mujeres y 74 en hombres.
En este caso no hay ningún valor atípico, es decir, ningún valor que
sobresalgan porque son mucho mayores o menores que los demás.

23. FIN.