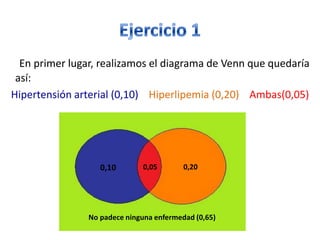
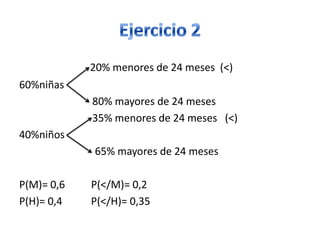
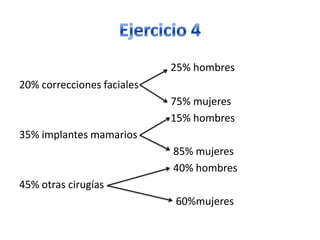
Este documento presenta varios ejercicios de probabilidad realizados en un seminario. El primer ejercicio calcula las probabilidades de padecer hipertensión arterial (A), hiperlipemia (B) o ambas enfermedades basado en porcentajes de pacientes. El segundo ejercicio calcula la probabilidad de que un paciente pediátrico sea menor de 24 meses usando porcentajes de niños, niñas y edades. Los ejercicios finales usan fórmulas de probabilidad condicionada y total para calcular diferentes probabilidades dados diferentes sucesos

2. En este seminario, repasamos probabilidad y para ellos
tenemos que realizar 4 ejercicios. El primero es el siguiente:
Un 15% de los pacientes atendidos en la Consulta de
Enfermería del Centro de Salud de el Cachorro padecen
hipertensión arterial (A) y el 25% hiperlipemia (B). El 5% son
hipertensos e hiperlipémicos .
• Cual es la P de A, de B y de la unión.
• Representa la situación en un diagrama de Venn.
• Calcula la probabilidad de que una persona al azar no padezca
ni A ni B

3. En primer lugar, realizamos el diagrama de Venn que quedaría
así:
Hipertensión arterial (0,10) Hiperlipemia (0,20) Ambas(0,05)
0,10 0,200,05
No padece ninguna enfermedad (0,65)

4. La P(A)= 0,15
La P(B)= 0,25
La P(A y B)= 0,05
P(Sano)= Ptotal – (P(A) + P(B) + P(A y B)=
P(1 - (0,1+0,05+0,2) )= 0,65 --> 65%

5. En la sala de pediatría de un hospital, el 60% de los
pacientes son niñas. De los niños el 35% son menores de
24 meses. El 20% de las niñas tienen menos de 24 meses.
Un pediatra que ingresa a la sala selecciona un infante al
azar.
• Determine el valor de la probabilidad de que sea menor
de 24 meses.
• Si el infante resulta ser menor de 24 meses. Determine
la probabilidad que sea una niña.

6. 20% menores de 24 meses (<)
60%niñas
80% mayores de 24 meses
35% menores de 24 meses (<)
40%niños
65% mayores de 24 meses
P(M)= 0,6 P(</M)= 0,2
P(H)= 0,4 P(</H)= 0,35

7. a) Se realiza mediante la fórmula de la probabilidad total
P(<)= P(H) x P(</H) + P(M) x P(</M) =
(0,4 x 0,35) + (0,6 x 0,2)=0,26 
b) Lo realizamos por el Teorema de Bayes
P(M/<)=
P(M/<)= 0,46 
26%
46%

8. Sean A y B dos sucesos aleatorios con p(A) = 1/2, p(B) = 1/3,
p(A∩B)= 1/4.
Determinar: P(A/B); P(B/A)
Este ejercicio se realiza por la fórmula de la probabilidad
condicionada:
P(A/B)= P(A∩B) / P(B)=0,25/0,33=
P(B/A)= P(A∩B) / P(A)= 0,25/0,5=
Se puede realizar esta operación sin tener P(B∩A) por la
propiedad conmutativa.
0,75
0,5

9. Un médico cirujano se especializa en cirugías estéticas. Entre
sus pacientes, el 20% se realizan correcciones faciales, un
35% implantes mamarios y el restante en otras cirugías
correctivas. Se sabe además, que son de genero masculino el
25% de los que se realizan correcciones faciales, 15%
implantes mamarios y 40% otras cirugías correctivas. Si se
selecciona un paciente al azar, determine:
a) Determine la probabilidad de que sea de género masculino
b) Si resulta que es de género masculino, determine la
probabilidad que se haya realizado una cirugía de implantes
mamarios.

10. 25% hombres
20% correcciones faciales
75% mujeres
15% hombres
35% implantes mamarios
85% mujeres
40% hombres
45% otras cirugías
60%mujeres

11. P(correcciones faciales)  P(F)= 0,2 P(H/F)= 0,25
P(implantes mamarios)  P(I)= 0,35 P(H/I)= 0,15
P(otras cirugías)  P(O)= 0,45 P(H/O)= 0,4
a) Utilizamos la fórmula de la probabilidad total:
P(H)= P(F) x P(H/F) + P(I) x P(H/I) + P(O) x P(H/O)
0,2 x 0,25 + 0,35 x 0,15 + 0,45 x 0,4= 0,2825 
b) Utilizamos el Teorema de Bayes
P(I/H)= = 0,1858 
28%
19%

12. FINAL