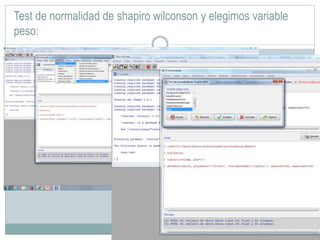
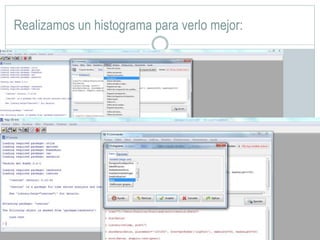
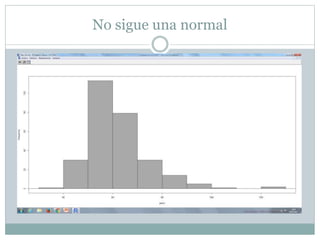
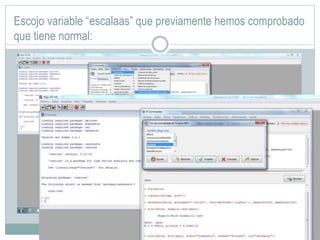
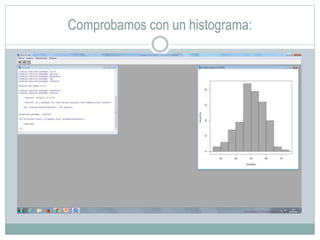
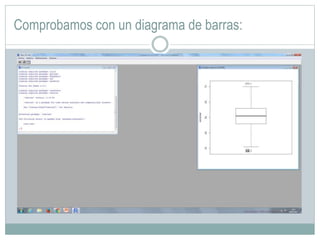
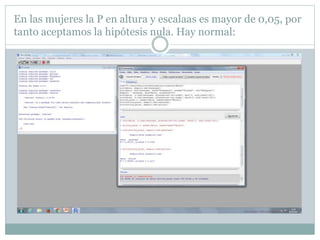
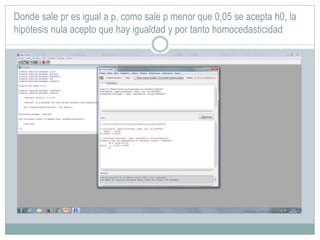
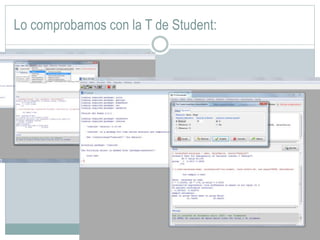
Este documento presenta un análisis bivariado de variables cualitativas y cuantitativas utilizando R. Se comprueba la normalidad de dos variables, "peso" y "escalaas", mediante pruebas estadísticas y gráficos. Luego, se divide la muestra en hombres y mujeres para comparar sus medias en "escalaas" y "altura" usando pruebas de normalidad, homocedasticidad y T de Student. Los resultados muestran que no hay diferencias significativas en "escalaas" entre sexos, pero sí las hay

1. A N Á L I S I S B I V A R I A D O : V A R I A B L E
C U A L I T A T I V A Y C U A N T I T A T I V A
P A T R I C I A G U Z M Á N G A R C Í A
SEMINARIO 8:

2. EJERCICIO:
 Comprobar la Normalidad de la variable
“escalaas”
 Usa test y gráficos

3. Abrimos R y cargamos la tabla de datos:

4. Test de normalidad de shapiro wilconson y elegimos variable
peso:

5. Como P es menor de 0,05 rechazo la hipótesis nula, y acepto que no hay
normal, no serviría utilizar la T de Student

6. Realizamos un histograma para verlo mejor:

7. No sigue una normal

8. Escojo variable “escalaas” que previamente hemos comprobado
que tiene normal:

9. P es mayor de 0,05, por tanto aceptamos la hipótesis nula, por
tanto si sigue una distribución normal

10. Comprobamos con un histograma:

11. Comprobamos con un diagrama de barras:

12. ¿La variable escala es igual a 45 o se parece?

13. Ahora rechazamos la hipótesis nula porque la P es mucho
menor que 45, nuestra media no se acerca a 45

14. Caso 2
 Compara medias de muestras independientes
 ¿ Chicos y chicas tienen la misma puntuación media en la
escalaas?
 ¿ Chicos y chicas tiene la misma altura media?
 ¿ Que diferencia hay en estos dos análisis?

15. Caso2: filtramos la base de datos en mujeres y hombres para
ver si hay diferencia:

16. En las mujeres la P en altura y escalaas es mayor de 0,05, por
tanto aceptamos la hipótesis nula. Hay normal:

17. Realizamos el mismo test con varones
 Se hace lo mismo con los hombres para ver si siguen
una normal
 Entonces sabemos que podemos hacer un test de
shapiro con los dos

18. Comprobamos la homocedasticidad:

19. Donde sale pr es igual a p, como sale p menor que 0,05 se acepta h0, la
hipótesis nula acepto que hay igualdad y por tanto homocedasticidad

20. Lo comprobamos con la T de Student:

21. La h0 es que no hay diferencia en la escalaas por sexo. Como la p es mayor de 0,05 aceptamos la
hipótesis nula, verificamos que no hay diferencias entre sexos

22. 2º caso: parte 2
 Usamos sexo y altura
 Realizo el test de Wilconson

23. La p es menor de 0,05, por tanto rechazo la hipótesis nula y acepto que
hay diferencias de alturas.

24. PATRICIA GUZMÁN GARCÍA