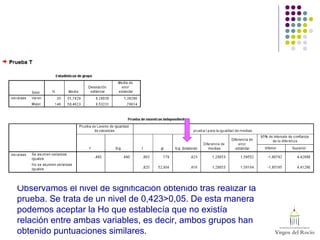
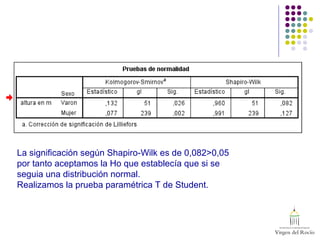
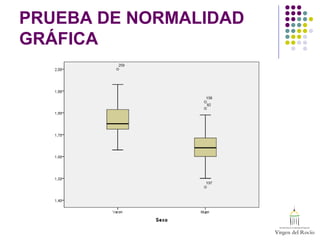
Este documento presenta el análisis estadístico de dos preguntas: 1) si existen diferencias en la puntuación promedio en una escala entre chicos y chicas, y 2) si existen diferencias en la altura promedio entre chicos y chicas. Para ambas preguntas, se realizan pruebas de normalidad gráfica y estadística, y pruebas t de Student para muestras independientes. Los resultados muestran que no hay diferencias significativas en la puntuación de la escala, pero sí las hay en la altura pro

2. T DE STUDENT
1. ¿Chicos y chicas tienen la misma
puntuación media en la escalas?
2. ¿Chicos y chicas tiene la misma altura
media?
Comprueba antes de elegir el test la
normalidad mediantes test estadístico y
representación gráfica y observa si se trata
de muestras apareadas o independientes.

3. PRIMERA PREGUNTA
Tenemos dos variables:
Sexo: variable cualitativa dicotómica
Escala: variable cuantitativa
Utilizaremos la prueba paramétrica T de
Student debido a las variables con las que
vamos a trabajar. Para ello hemos de
comprobar si la variable “Escala” sigue una
distribución normal. Realizaremos una prueba
de normalidad.

4. ABRIMOS LA MATRIZ DE DATOS
 Ho: Sigue una distribución normal (p>0,05)
 H1: No hay distribución normal (p<0,05)

5. REALIZAMOS LA PRUEBA DE
NORMALIDAD
Analizar-Estadísticos Descriptivos-Explorar
Al clickear en “Gráficos de normalidad
con pruebas” permitimos que se
compruebe si la variable sigue o no una
distribución normal.

6. El nivel de significación obtenido (por la prueba de Shapiro-
Wilk) es de 0,231>0,05.
De esta manera apoya la hipótesis nula y con ello podemos
aceptar que sigue una distribución normal.
Ahora podemos utilizar con seguridad la T de Student

7. PRUEBA DE NORMALIDAD
GRÁFICA

8. PRUEBA T DE STUDENT
Analizar-Comparar medias-Prueba T para muestras
independientes
En la variable de prueba hemos
seleccionado nuestra variable
cuantitativa “escala” y en
variable de agrupación “sexo”.
Ho: no existe relación entre el sexo
y la puntuación de escala obtenida
H1: si hay relación entre ambas

9. Observamos el nivel de significación obtenido tras realizar la
prueba. Se trata de un nivel de 0,423>0,05. De esta manera
podemos aceptar la Ho que establecía que no existía
relación entre ambas variables, es decir, ambos grupos han
obtenido puntuaciones similares.

10. SEGUNDA PREGUNTA
 Sexo: variable cualitativa dicotómica
 Altura: variable cuantitativa
Ho: sigue una distribución normal
H1: no hay una distribución normal

11. PRUEBA DE NORMALIDAD

12. La significación según Shapiro-Wilk es de 0,082>0,05
por tanto aceptamos la Ho que establecía que si se
seguia una distribución normal.
Realizamos la prueba paramétrica T de Student.

13. PRUEBA DE NORMALIDAD
GRÁFICA

14. T DE STUDENT
En este caso el nivel de significación es de 0, por tanto al ser < 0,05
debemos aceptar la H1 que establecía que si existía relación entre el
sexo y la altura.
Podemos concluir, observando la media de la altura, que los varones
presentan una altura media mayor que las mujeres.