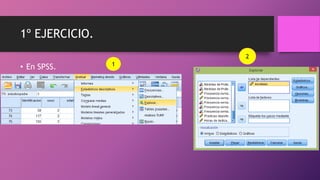
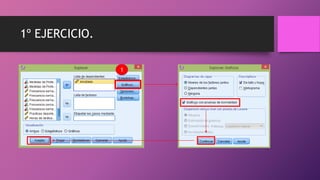
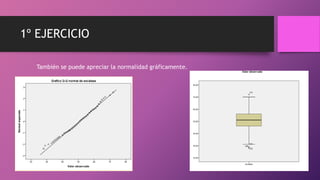
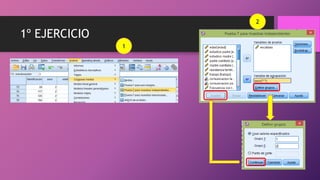
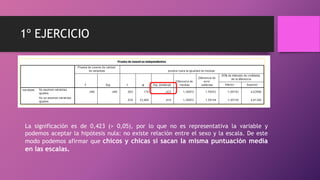
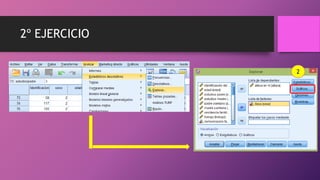
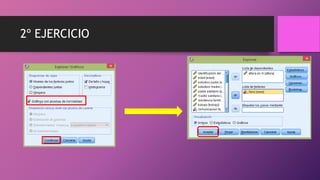
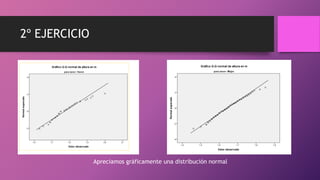
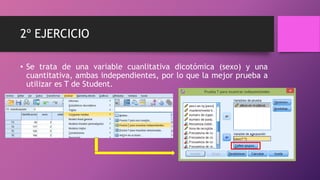
Este documento presenta dos ejercicios para determinar si chicos y chicas tienen la misma puntuación media en escalas y la misma altura media. En el primer ejercicio, se utiliza la prueba t de Student y se determina que chicos y chicas tienen la misma puntuación media en las escalas. En el segundo ejercicio, también se usa la prueba t de Student y se concluye que chicos y chicas no tienen la misma altura media, siendo la altura media de los chicos mayor que la de las chicas.

1. T DE STUDENT
ELENA PÉREZ TORREJÓN

2. DATOS
• AVERIGUAR:
1. Chicos y chicas tienen la misma puntuación media en la escalas
2. Chicos y chicas tienen la misma altura media
Comprueba antes de elegir el test la normalidad mediante test
estadístico y representación gráfica y observa si se trata de
muestras apareadas o independientes

3. Ejercicio 1

4. 1º EJERCICIO.
• Chicos y chicas tienen la misma puntuación media en la escalas.
Se establecen dos hipótesis:
H0: Los chicos y chicas tienen la misma puntuación media en las escalas. Se distribuye
normalmente.
H1: Los chicos y chicas tienen distinta puntuación media en las escalas. No se
distribuye normalmente.
Como el sexo es una variable dicotómica sólo se analiza la normalidad en la variable
cuantitativa

5. 1º EJERCICIO.
• En SPSS. 1
2

6. 1º EJERCICIO.
1

7. 1º EJERCICIO.
Como el resultado es de 0,231 (> 0,05) se aceptaría la hipótesis
nula, por lo que la variable se distribuye normalmente.

8. 1º EJERCICIO
También se puede apreciar la normalidad gráficamente.

9. 1º EJERCICIO
• Se trata de dos variables independientes: una cuantitativa
(escalas) y una cualitativa dicotómica (sexo).
La mejor prueba a utilizar sería por tanto: T de Student.

10. 1º EJERCICIO
1
2

11. 1º EJERCICIO
La significación es de 0,423 (> 0,05), por lo que no es representativa la variable y
podemos aceptar la hipótesis nula: no existe relación entre el sexo y la escala. De este
modo podemos afirmar que chicos y chicas sí sacan la misma puntuación media
en las escalas.

12. Ejercicio 2

13. 2º EJERCICIO
• Chicos y chicas tienen la misma altura media
Se establecen 2 hipótesis:
H0: Chicos y chicas tienen la misma altura media. Se distribuye
normalmente.
H1: Chicos y chicas tienen distinta altura media. No se distribuye
normalmente.
De nuevo se trata de una variable cualitativa dicotómica y una
cuantitativa por lo que analizaremos sólo la normalidad de la cualitativa.

14. 2º EJERCICIO
2

15. 2º EJERCICIO

16. 2º EJERCICIO
La significación es de 0,082 (> 0,05) por lo que se aceptaría
la hipótesis nula y presentaría una distribución normal.

17. 2º EJERCICIO
Apreciamos gráficamente una distribución normal

18. 2º EJERCICIO
• Se trata de una variable cuanlitativa dicotómica (sexo) y una
cuantitativa, ambas independientes, por lo que la mejor prueba a
utilizar es T de Student.

19. 2º EJERCICIO
Aceptar

20. 2º EJERCICIO
La significación es < 0,05 por lo que podríamos rechazar la hipótesis
nula y afirmaríamos que existe relación entre la altura el sexo.

21. 2º EJERCICIO
La altura media de los chicos es de 1,7731 y la
de las chicas es de 1,6444. de este modo
podemos decir en respuesta a la pregunta que
los chicos y chicas no tienen la misma
altura media.