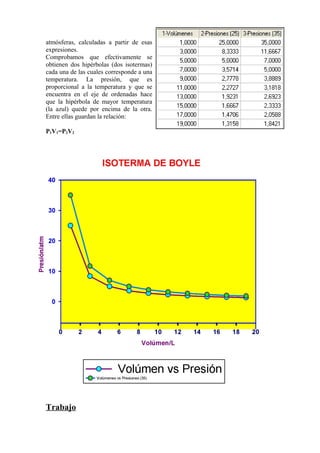
Robert Boyle fue un químico inglés del siglo XVII que realizó importantes estudios sobre los gases. En 1661 enunció la ley que lleva su nombre, la cual establece que para una temperatura dada, el producto de la presión y el volumen de un gas permanece constante. Más tarde, Boyle utilizó esta ley para estudiar experimentalmente la relación entre la presión y el volumen de los gases, representando sus resultados en curvas llamadas isotermas que ilustran cómo varía la presión de un gas a medida que cambia su volumen a una temper

1. SEMINARIO DE REPRESENTACIÓN GRÁFICA
Boyle y sus estudio sobre los gases
Robert Boyle era un químico inglés del siglo XVII (1627-1691) que pasó toda su vida
estudiando la ciencia y sus aplicaciones.
Muchos lo consideraban el fundador de la
química moderna pues dejaba atrás el
concepto de alquimia y proponía el estudio de
la química como una ciencia independiente de
la medicina.
Fue el primero que definió claramente
“elementos químicos” como: “ciertos cuerpos
primitivos y simples o perfectamente exentos
de toda mezcla; los cuales, al no estar hechos de
cualesquiera otros cuerpos o uno de otro, son
los ingredientes de los que están compuestos de
forma inmediata todos aquellos otros llamados
cuerpos perfectamente mezclados y en los que
estos últimos se descomponen” (Sceptical
Chymist,1661).
Son de citar los estudios que realizó sobre los
ácidos y los álcalis, de los que describió
numerosas propiedades.
Boyle, fue también el primero en demostrar de manera experimental que los gases pueden
recogerse en recipientes. Estudió los efectos de la presión sobre el aire, lo que le llevó en
1661 a enunciar la ley que lleva su nombre y que indica que para una temperatura
determinada, el producto de la presión por el volumen de un gas permanece constante.
A esta ley se la conoce también con el nombre de Mariotte, pero éste no la publicó hasta
1679 y nunca dijo que fuese original.
Ley de Boyle Mariotte para los gases ideales:
PV=K
Por tanto, la presión es inversamente proporcional al volumen o viceversa.
P=K/V
V=K/P
Estas dos expresiones corresponden a la ecuación de una hipérbola en la que la
temperatura permanece constante y se llama isoterma. Así, definimos una isoterma
como una curva que ilustra la variación en la presión de una muestra de gas con el
cambio de volumen.
En el seminario de representaciones gráficas vamos a calcular el trabajo de un sistema, a
partir de la elaboración de una isoterma.
Para ello usamos el programa “Sigma Plot” y diseñamos unas isotermas a partir de una
tabla que elaboramos aplicando la ley de Boyle :
PxV=25 y PxV=35 con volúmenes aleatorios en litros y presiones en

2. atmósferas, calculadas a partir de esas
expresiones.
Comprobamos que efectivamente se
obtienen dos hipérbolas (dos isotermas)
cada una de las cuales corresponde a una
temperatura. La presión, que es
proporcional a la temperatura y que se
encuentra en el eje de ordenadas hace
que la hipérbola de mayor temperatura
(la azul) quede por encima de la otra.
Entre ellas guardan la relación:
P1V1=P2V2
Trabajo

3. Se efectúa trabajo P-V sobre un sistema termodinámico cuando se produce un cambio
de volumen del sistema. Al aplicar una presión exterior diferente, el gas se expandirá o
comprimirá dependiendo si ésta es mayor o menor que la presión del sistema.
En la representación de una isoterma de Boyle, el área bajo la curva corresponde al
trabajo.
Cuando consideramos toda el área bajo la curva, obtenemos el trabajo máximo posible,
el trabajo reversible. Así el trabajo reversible se define como la cantidad máxima de
trabajo que puede obtenerse cuando un sistema experimenta un proceso entre los
estados inicial y final. En este caso, la presión del gas debe ser en todo momento
infinitesimalmente diferente a la presión externa. A cada instante el sistema se
encuentra en una especie de equilibrio termodinámico y si se cambian las condiciones
externas es posible invertir el sentido de la evolución. Se deduce entonces que en un
proceso reversible la presión y la temperatura se consideran uniformes en todo
momento.
Podemos calcular el trabajo reversible de una de las isotermas en un solo paso (en
infinitas etapas). Para ello calculamos el área bajo la hipérbola de color morado:
Utilizamos la expresión
2 2 dV V P
wrev = −∫ PdV = −nRT ∫ = nRT ln 1 = nRT ln 2
1 1 V V2 P1
Sustituímos nuestros datos:
nRT= 25
P1=25atm
P2=1,3158atm
1,3158 atm
wrev = 25 atm × L × ln = −73 ,61atm × L
25 atm
Expresamos el resultado en Julios:
101 ,3 J
− 73 ,61atm × L = −7456 ,77 J
1atm × L
Por otra parte definimos el trabajo irreversible como el trabajo correspondiente a un
proceso que se realiza a través de algún estado de no equilibrio. Esto no significa que el
sistema no pueda volver a su estado inicial sino que, el medio no puede hacerlo
simultáneamente.
Podemos calcular el trabajo irreversible en uno o varios pasos, trazando en la isoterma
uno o varios rectángulos y calculando su área. El trabajo irreversible debe salir menor
que el reversible (en valor absoluto).
En primer lugar calculamos el trabajo irreversible en un sólo paso.

4. 2
w = −∫ PdV = −Pext (V2 −V1 )
1
w = −1,3158 atm (19 L −1L ) = −23 ,68 atmxL
Pasamos a Julios:
101 ,3 J
− 23 ,68 atm × L = −2399 ,22 J
1atm × L
Calcularemos ahora el trabajo irreversible en dos pasos. Para ello trazamos dos
rectángulos bajo la curva.

5. w = −∑ PdV = ∑ − Pext (V2 − V1 )
2
∫1
w = −[ (1,3158 atm (19 L − 9 L) ) + ( 2,7778atm( 9L - 1L) ) ] = −35,38 atmxL
Pasamos a Julios:
101 ,3 J
− 35 ,38 atm × L = −3584 ,03 J
1atm × L

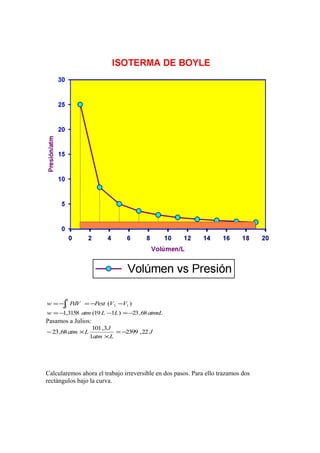
6. Calcularemos finalmente el trabajo irreversible en tres pasos. Para ello trazamos tres
rectángulos bajo la curva.
w = −∑ PdV = ∑ − Pext (V2 − V1 )
2
∫1
w = −[ (1,3158 atm (19 L − 15 L) ) + (1,6667atm( 15L - 5L) ) + ( 5atm (5 L − 1L ) ] = −41,93atmxL

7. Pasando a Julios:
101 ,3 J
− 41,93 atm × L = −4247 ,53 J
1atm × L
COMPARACIÓN DE RESULTADOS Y CONCLUSIÓN
Podemos comprobar que como preveíamos, cuando el trabajo se calcula en
infinitas etapas ( proceso reversible) el valor obtenido es mayor (en valor
absoluto) que cuando lo calculamos en una, dos o tres etapas (proceso
irreversible).
Además cuando calculamos el trabajo irreversible en un paso, éste sale menor
que cuando lo calculamos en dos pasos y este a su vez, es menor que cuando lo
calculamos en tres pasos (todo en valor absoluto). Esto es lógico, porque el área
calculada es mayor.
Concluimos que una isoterma de Boyle, es un buen método para calcular el
trabajo de un sistema, empleando el recurso de la representación gráfica.