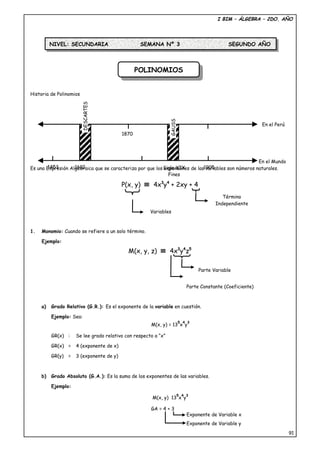
Este documento trata sobre polinomios. Define un polinomio como una expresión algebraica cuyos exponentes de las variables son números naturales. Explica que un monomio es un solo término de un polinomio, mientras que un polinomio es la agrupación por adición de monomios no semejantes. Además, introduce conceptos como el grado relativo, grado absoluto y valor numérico de un polinomio o monomio.