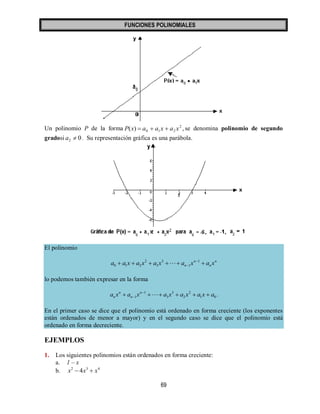
Este documento trata sobre funciones polinomiales. Define funciones polinomiales y monomiales, y explica cómo realizar operaciones como suma, resta, multiplicación y división con polinomios y monomiales. También cubre conceptos como grado de un polinomio/monomio, reducción de términos semejantes, y ordenar polinomios en forma creciente y decreciente. Finalmente, presenta ejemplos y ejercicios para practicar estas operaciones con polinomios.








![FUNCIONES POLINOMIALES
75
4. Encontrar el área de cada uno de los siguientes rectángulos por adición de las áreas de los
rectángulos pequeños.
5. Factorizar los siguientes polinomios:
a) 2ax + 3a b) 25 t³ 75t² 45t
c) x² 2x + 1 d) t² 1.2t + 0.36
e) x² 1 f) x³ 1
g) x³ + 1 h) x4 1
i) ( x + 1 )³ x³ 1
6. Dados los polinomios p(x) = 3x4 x² + 5, q(x) = 2x³ + x² 5 y r(x) = 3x³. Ordene los
siguientes polinomios según las potencias decrecientes de x.
a) p(x) + 4q(x) + 5r(x)=
b) p(x) q(x) + 3r(x)=
c) p(x) + 2q(x) 2r(x)=
d) p(x)× q(x) =
e) [p(x)]² [q(x)]² =
f) [p(x)]²[q(x)]² + [r(x)]³ =
7. Exprese como an xⁿ + …+ a1 x + a0 :
a) (2x + 3)(x² + 1) + (x 1)(x 2)
b) x(x + 1)(x² + 1) (2x + 1)(2x 1)
c) (x + a)(x + b)
d) (x + a)(x + b) (x + a )(x + c)
e) (x² + 1)(2x 1) (x² + 1)(x² + 2)
f) (x + 2)²(x + 4) x(x² + 4x + 6) + 5(x 1)(2x 1)
g) (x + 2)²(x² + 1) + x(x + 2)(x + 3) + (x + 2)(3x² 5x 5)
h) (x + 1)(x + 2)(x + 3)(x + 4) x(x + 1)(x + 2)(x + 3)](https://image.slidesharecdn.com/segundocaptulo2-141129153112-conversion-gate01/85/LAS-FUNCIONES-POLINOMIALES-11-320.jpg)








![FUNCIONES POLINOMIALES
84
Se tiene entonces que q(x) = 2x3 –ax2 –a2x –3a3y r(x) = 0. En este caso, el polinomio p(x)
es divisible por el polinomio q(x) = x – a.
EJERCICIOS.
Aplicando la regla de Ruffini, calcular el cociente y el residuo de las siguientes divisiones.
1. (2x ) 2 + 3x – 3 (x + 2 )
2. (3x ) 2 + 5x – 7 ( x + 3)
3. (x ) 3 + x2 – 6x + 7 ( x – 1)
4. 2y3 + 5y2 – 4y – 1 y + 3
5. (x ) 4 –5ax3 + 6a2x2 + a3x- 3a4 (x – 3a)
6.
3x2 –
77
10
x +
5
6
x –
5
2
7.
3
4
x2 - x + 1
x –
2
3
8.
3
5
x2 –
13
6
bx + b2
x –
5
2
b
9.
2
3
x3 –
3
2
x2 +
13
12
x – 1
x –
3
2
10.
3
5
x4 –
3
10
x3 –
1
2
x2 +
9
4
x – 1
x –
1
2
11.
3
2
x4 +
1
2
bx3 –
1
3
b2x2 +
1
9
b4
x +
b
3
12. (ax ) 3 + b(a + b)x2 – a(a + b)2x – b(a + b)3 (x – a - b)
13. [x ] 3 – c x2 – (a + b)2x – c(a + b)2 (x – a – b – c )
14. [x ] 3 – (a + b +c) x2 + (ab + bc + ac)x – abc [ (x – a) (x – b)]
Extensión de la regla de Ruffini al caso en el cual el divisor es un binomio
del tipoax – b
Si queremos dividir un polinomio p(x) por un binomio del tipo ax – b, de la relación
fundamental
p(x) = q(x) (ax - b) + r
dividiendo ambos miembros por a, obtenemos:](https://image.slidesharecdn.com/segundocaptulo2-141129153112-conversion-gate01/85/LAS-FUNCIONES-POLINOMIALES-20-320.jpg)

![FUNCIONES POLINOMIALES
86
7.
3
2
x3 – 5 x2 +
55
24
x +
5
8
3
2
x - 4
8. [ax ] 3 + (1 – a ) 2 x2 – 1 (ax + 1)
9.
2
3
2 1 .
a b b a
x x x
b a a b
EL TEOREMA DEL RESIDUO
Dado un polinomio cualquiera p(x), sabemos que:
p(x) = (x – a) q(x) + r.
La identidad precedente es válida para todo número real x, en particular para x a. Se tiene
entonces que:
( ) ( )
0 ( )
.
p a a a q x r
q a r
r
es decir que: p(a) r; que expresa el siguiente resultado, que recibe el nombre de teorema
del residuo.
El residuo de la división de un polinomio p(x) por el binomio x – a es igual al valor
que asume el polinomio p(x) en x = a.
El teorema permite encontrar directamente el residuo de la división, sin tener que realizar
toda la división.
Así por ejemplo, el residuo de la división del polinomio p(x) = 2x3 – 5x2 + 3x – 4 por el
binomio x – 1 es r = p(1) = 2 13 – 5 12 + 3 1 – 4 = 4 .
El residuo de la división del polinomio p(x) = x4 + 2x3 + 5x – 18 por el binomio x + 3 es:
r = p( 3) = ( 3)4 + 2( 3)3 + 5( 3) – 18 = 81 – 54 – 15 –18 = 6.
La utilidad del teorema del residuo radica en que nos permite establecer cuándo un
polinomio p(x) es divisible por el binomio x k.
Se tiene el siguiente criterio de divisibilidad:
Condición necesaria y suficiente para que un polinomio p(x) sea divisible por el
binomio x – k, es quep(k) = 0.
En símbolos:
(x – k) | p(x) p(k) = 0,](https://image.slidesharecdn.com/segundocaptulo2-141129153112-conversion-gate01/85/LAS-FUNCIONES-POLINOMIALES-22-320.jpg)

