Este documento presenta 15 problemas de trigonometría relacionados con ángulos y sectores circulares. Los problemas involucran calcular longitudes de arcos, áreas de sectores y relaciones entre radios y longitudes de arcos. El documento proporciona las soluciones detalladas para cada problema utilizando conceptos básicos de trigonometría como la relación entre la longitud del arco y el radio del círculo.

![[ÁNGULO TRIGONOMÉTRICO]
3 TRIGONOMETRÍA | LIC. RODOLFO CARRILLO VELASQUEZ
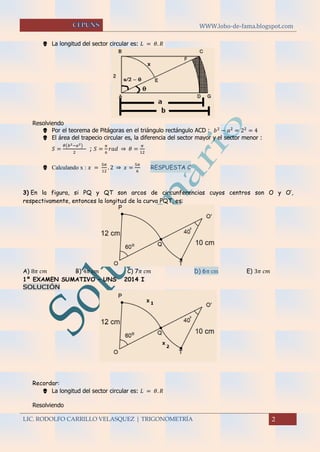
Según los datos :𝑥 = 𝑥1 + 𝑥2
Reemplazando: 𝑥 = 12 ∗ 60º ∗
𝜋
180º
+ 10 ∗ 40 𝑔
∗
𝜋
200 𝑔 ⇒ 𝑥 = 6𝜋 𝑐𝑚 RESPUESTA D
4) En la figura , si los perímetros de los sectores circulares son equivalentes, entonces el valor de
“𝜃” es:
A)
(π−2)
2
B)
(𝜋−2)
3
C)
(𝜋−2)
5
D) (𝜋 − 2) E) 𝜋
1º EXAMEN SUMATIVO – UNS 2013 III
SOLUCIÓN
Recordar:
La longitud del sector circular es: 𝐿 = 𝜃. 𝑅
El perímetro es : 𝑃 = 2𝑅 + 𝐿
Resolviendo
Según los datos :𝑃1 = 2𝑅 + 𝐿1 y 𝑃2 = 2(2𝑅) + 𝐿2
Reemplazando: 2(2𝑅) + 2𝑅 ∗ 𝜃 = 2𝑅 + (𝜋 − 𝜃) ∗ 2𝑅
2𝑅 + 4𝑅𝜃 = 2𝜋𝑅 ⇒ 𝜃 =
𝜋−2
3
RESPUESTA B
5) En un círculo se inscribe un triángulo isósceles, el ángulo formado por los lados congruentes
mide 14º y la base intercepta un arco de longitud 66m. Calcular la longitud del radio de dicho
círculo. ( Considerar
7
22
)
a) 140m b) 270m c) 40m d) 135m e) 120m
1º EXAMEN SUMATIVO – UNS 2013 II
SOLUCIÓN](https://image.slidesharecdn.com/solucionariosemana22-170419212415/85/Solucionario-semana-2-2-3-320.jpg)

![[ÁNGULO TRIGONOMÉTRICO]
5 TRIGONOMETRÍA | LIC. RODOLFO CARRILLO VELASQUEZ
a) x – y b) 2( x - y ) c) 2( y - x ) d) 4 ( x – y ) e) 4( y - x)
1º EXAMEN SUMATIVO – UNS 2013 I
SOLUCIÓN
Recordar:
El área del sector circular es: 𝑆 =
𝜃.𝑅2
2
Resolviendo
Según los datos, los sectores circulares AOB y COD , tiene igual área : 𝑆 =
𝑥∗22
2
Reemplazando en el sector circular OBE: 𝑆 + 𝐴𝑠 =
𝑦∗22
2
⇒ 𝐴𝑠 = 2(𝑦 − 𝑥) RESPUESTA D
8) Calcule: 2 3
1
S S
M
S
Donde S1, S2 y S3 son las áreas de las regiones sombreadas
S2
S1
S3
2
A) 12
7
B)
13
2 C) 1
12
D) 5 + 2 E) 5 2
SOLUCIÓN
Resolviendo
Según los datos 𝑀 =
𝑆2+𝑆3
𝑆1
=
3𝑘+10𝑘
2𝑘
⇒ 𝑀 =
13
2
RESPUESTA B
9) Del gráfico, determinar
NMP
BA
L
L
, Si AOB es sector circular.](https://image.slidesharecdn.com/solucionariosemana22-170419212415/85/Solucionario-semana-2-2-5-320.jpg)

![[ÁNGULO TRIGONOMÉTRICO]
7 TRIGONOMETRÍA | LIC. RODOLFO CARRILLO VELASQUEZ
Recordar:
La longitud del sector circular es: 𝐿 = 𝜃. 𝑅
Resolviendo
Según los datos : 𝜃 =
80
𝑅
=
45
𝑟
⇒
𝑟
𝑅
=
9
16
Reemplazando : 𝐹 = 16 (
9
16
) − 2 = 7 RESPUESTA A
11) Se tiene un sector circular cuya longitud de arco es numéricamente igual a la mitad del
área de un cuadrado, cuyo lado es igual al radio del sector. ¿Cuánto mide la longitud de arco del
sector, si la medida del ángulo central expresado en radianes, toma su mayor valor entero posible?
A) 12 B) 24 C) 48 D) 72 E) 144
SOLUCIÓN
Recordar:
La longitud del sector circular es: 𝐿 = 𝜃. 𝑅
Resolviendo
Según los datos : 𝐿 =
𝑅2
2
; 𝜃. 𝑅 =
𝑅2
2
⇒ 𝑅 = 2𝜃 y 𝐿 =
𝑅2
2
Reemplazando : 𝐿 = 2𝜃2
, 𝐿 = 2 ∗ 62
⇒ 𝐿 = 72 RESPUESTA D
12) En la figura se muestran las A1, A2 y A3, que están en progresión aritmética, además
, y
Calcular:
A) ½ B) 2/3 C)2 D) 3 E) 3–1
SOLUCIÓN
Recordar:
La longitud del sector circular es: 𝐿 = 𝜃. 𝑅
EF
L a CD
L b AB
L c
2 2
2
b a
c
E
C
A
F
D
B
A1
A3](https://image.slidesharecdn.com/solucionariosemana22-170419212415/85/Solucionario-semana-2-2-7-320.jpg)

![[ÁNGULO TRIGONOMÉTRICO]
9 TRIGONOMETRÍA | LIC. RODOLFO CARRILLO VELASQUEZ
15) A partir del gráfico, calcular la longitud recorrida por la esferita, hasta impactar en CD. Si
AB = BC = 4m. longitud de la rueda es 10m.
a) 5 m b) 5/2 m c) 2 m d) 3/2 m e) 8 m
SOLUCIÓN
Recordar:
La longitud del sector circular es: 𝐿 = 𝜃. 𝑅 , además 𝐿 𝐴 = 𝐿 𝐵
Resolviendo
Según los datos : 𝐿 = 𝐿1 + 𝐿2 + 𝐿3
Reemplazando : 𝐿 =
𝜋
3
∗ 10 +
𝜋
6
∗ 6 +
𝜋
3
∗ 2 ⇒ 𝐿 = 5𝜋 𝑚 RESPUESTA A
16) En el grafico mostrado r = 1 y R = 3 , además O es el centro del sector circular AOB,
entonces el perímetro de la región sombreada es:
a) b)
3
11 c)
3
5 d)
3
7 e)
SOLUCIÓN](https://image.slidesharecdn.com/solucionariosemana22-170419212415/85/Solucionario-semana-2-2-9-320.jpg)

![[ÁNGULO TRIGONOMÉTRICO]
11 TRIGONOMETRÍA | LIC. RODOLFO CARRILLO VELASQUEZ
A) B) C) D) E)
SOLUCIÓN
Primero dividimos 1305° entre 360° , lo cual indica que da dos vueltas y queda como residuo 225° , por lo
tanto la altura seria : 𝐻 = 𝑅 +
𝑅√2
2
⇒ 𝐻 =
𝑅
2
(2 + √2)
RESPUESTA D
PROBLEMA DE REPASO
1) Determine el número de vueltas que da la rueda de ir de A hacia B. Si AC = CE = 9r/2 , R = 9r
A) 6 B) 5 C) 3 D) 8 E) 9
SOLUCIÓN
Resolvemos 𝑁𝑉 =
𝐿 𝑐
2𝜋𝑟
=
𝑎+𝑏+𝑐+𝑑
2𝜋𝑟
⇒ 𝑁𝑉 =
9𝜋𝑟
2
+
𝜋𝑟
3
+
9𝜋𝑟
2
+
8𝜋𝑟
3
2𝜋𝑟
R
A
2 1 R
1 2 2
R
2
1 2 2
R
2
2 2
R
2
2 2 1
R
2
](https://image.slidesharecdn.com/solucionariosemana22-170419212415/85/Solucionario-semana-2-2-11-320.jpg)

![[ÁNGULO TRIGONOMÉTRICO]
13 TRIGONOMETRÍA | LIC. RODOLFO CARRILLO VELASQUEZ
𝑁 𝑉 =
( 𝑅 + 𝑟)
𝜋
3
+ ( 𝑅 − 𝑟)
2𝜋
3
2𝜋𝑟
⇒ 𝑁 𝑉 =
3𝑅 − 𝑟
6𝑟
RESPUESTA E
5) Determinar el valor de “L”
A) 3 B)6 C) 12 D) 15 E) 10
SOLUCIÓN
Recordar:
La longitud del ángulo, es : 𝜃 =
𝐿1−𝐿2
𝑛
Resolviendo
Según los datos :
𝐿−4
3
=
14−𝐿
2
Reemplazando : 𝑋 = 10 RESPUESTA E
6) En la figura, ABC es un triángulo equilátero de 18cm de perímetro. Hallar la longitud de la curva que une
los puntos D,E,F, y B, sabiendo que BAF, FCE y EBD son sectores circulares.
A) 12cm B) 16 cm C)18cm D)24 cm E) 30 cm
SOLUCIÓN
Como el perímetro es 18 el lado del triángulo es 6cm.
𝐿 = (6 + 12 + 18 )(
2𝜋
3
) = 24𝜋 RESPUESTA D
7) Los radios de las ruedas de una bicicleta, son entre sí como 3 es a 4. Calcular el número de
vueltas que da la rueda mayor cuando la rueda menor gire 8 radianes.
A) 2 B) 3 C) 4 D) 6 E) 8
SOLUCIÓN
Recordar:
La longitud del sector circular es: 𝐿 = 𝜃. 𝑅 , además 𝐿 𝐴 = 𝐿 𝐵
Calculo del número de vueltas : 𝑁𝑉 =
𝐿
2𝜋𝑅
Resolviendo
Según los datos : 𝐿 𝐴 = 𝐿 𝐵
Reemplazando : 4𝜃 = 3 ∗ 8𝜋 → 𝜃 = 6𝜋](https://image.slidesharecdn.com/solucionariosemana22-170419212415/85/Solucionario-semana-2-2-13-320.jpg)
![[ÁNGULO TRIGONOMÉTRICO]
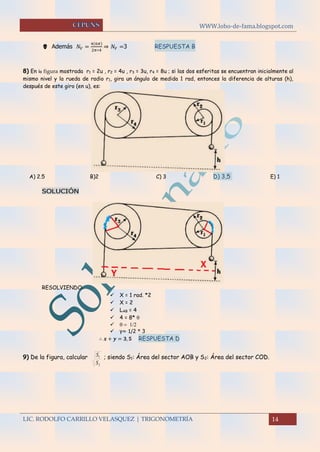
15 TRIGONOMETRÍA | LIC. RODOLFO CARRILLO VELASQUEZ
a)
ba
a
b)
ba
a
c)
ba
a
2
d)
ba
a
2
e)
ba
a
2
SOLUCIÓN
Calculo de las áreas: 𝑆1 =
𝜃𝑎2
2
𝑆2 =
𝜃(𝑎−2𝑏)2
2
Calculamos: ∴ √
𝑆1
𝑆2
=
𝑎
𝑎−2𝑏
RESPUESTA C
10) De la figura mostrada determinar el número de vueltas que da la rueda de radio “r” en su
recorrido de A hasta B (R=7r).
A) 2 B) 3 C) 4 D) 5 E) 6
SOLUCIÓN
𝑁𝑉 =
𝐿 𝑐
2𝜋𝑟
=
3𝜋
4
(8𝑟)
2𝜋𝑟
= 3
RESPUESTA B
11) Cuánto avanza la rueda de la figura adjunta si el punto “A” vuelve a tener contacto otras 7
veces y al detenerse el punto “B” está es contacto con el piso (r=12u).
135º
R
R
A
B
r
r](https://image.slidesharecdn.com/solucionariosemana22-170419212415/85/Solucionario-semana-2-2-15-320.jpg)
