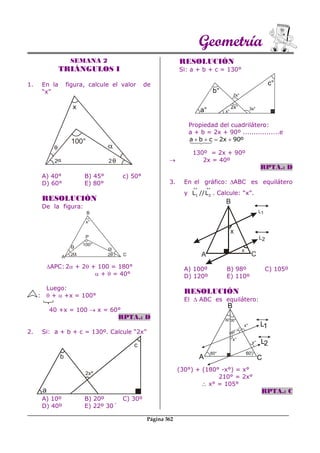
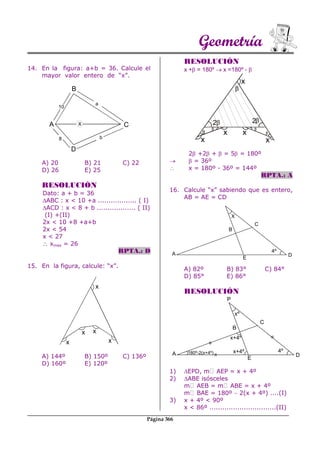
Este documento presenta 20 problemas de geometría sobre triángulos. Cada problema incluye una figura, datos y una resolución que conduce a una respuesta. Los problemas cubren temas como ángulos, lados, bisectrices y propiedades de triángulos isósceles y equiláteros.