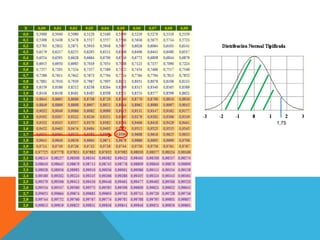
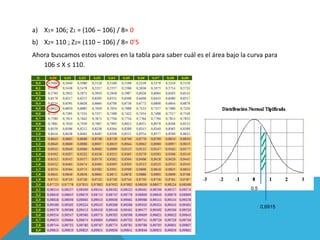
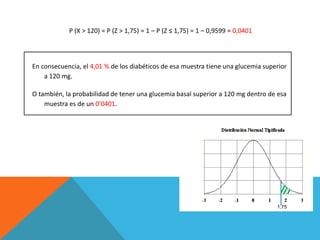
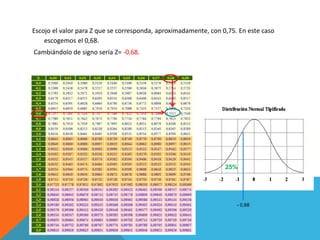
Este documento presenta 4 ejercicios estadísticos sobre la glucemia basal de diabéticos atendidos en una consulta de enfermería. Los ejercicios calculan: 1) la proporción con glucemia ≤ 120 mg/100ml (95.99%), 2) la proporción entre 106-110 mg/100ml (19.15%), 3) la proporción > 120 mg/100ml (4.01%), 4) el primer cuartil es 100.56 mg/100ml. En todos los casos se asume una distribución normal de la glucemia con media 106 mg/100

1. ESTADÍSTICA Y TICS
EJERCICIO OBLIGATORIO
SEMINARIO 7
M A R Í A J O S É J U R A D O C O R PA S
G R U P O 3 - VA L M E
C U R S O 2 0 1 4 - 2 0 1 5

2. 3.1. Calcula la proporción de diabéticos con una glucemia basal inferior o igual a 120.
Datos:
P (X ≤ 120)
Media = = 106
Desviación típica = σ = 8
Para resolver este ejercicio, lo primero que tenemos que hacer es tipificar el valor de la
variable (Z) para poder buscarlos en la tabla de la distribución normal.
Para ello utilizaremos la siguiente fórmula:
Z = (X - ) / σ = (120 – 106) / 8 = 1’75
Ahora buscamos este valor en la tabla para saber el área de la curva por debajo de Z, es
decir, ¿cuál es el área bajo la curva para X ≤ 120?
La glucemia basal de los diabéticos atendidos en la consulta de
enfermería puede considerarse como una variable normalmente
distribuida con media 106 mg por 100ml y desviación típica de 8 mg
por 100 ml N (106;8)

3. h
1,75

4. Mediante la tabla obtenemos que P (Z ≤ 1’75) = P (X ≤ 120) = 0’9599
En consecuencia, el 95’99 % de los diabéticos de esa muestra tiene una glucemia
inferior o igual a 120 mg.
O también, la probabilidad de tener una glucemia basal inferior o igual a 120 mg
dentro de esa muestra es de un 0’9599.

5. 3.2. La proporción de diabéticos con una glucemia basal comprendida entre 106 y 110
mg por ml.
Datos:
P (106 ≤ x ≤ 110)
Media = = 106
Desviación típica = σ = 8
Para resolver este ejercicio, tenemos que tipificar ambos valores de la variable para
poder buscarlos en la tabla de la distribución normal, como en el ejercicio anterior.
Para ello utilizaremos la misma fórmula:
Z = (X - ) / σ
La glucemia basal de los diabéticos atendidos en la consulta de
enfermería puede considerarse como una variable normalmente
distribuida con media 106 mg por 100ml y desviación típica de 8 mg
por 100 ml N (106;8)

6. a) X1= 106; Z1 = (106 – 106) / 8= 0
b) X2= 110 ; Z2= (110 – 106) / 8= 0’5
Ahora buscamos estos valores en la tabla para saber cuál es el área bajo la curva para
106 ≤ X ≤ 110.
0,6915
0,5

7. Mediante la tabla obtenemos que
P (0 ≤ Z ≤ 0’5) = P (106 ≤ X ≤ 110) = P (Z ≤ 0,5) – P( Z ≤ 0) = 0,6915 - 0,5= 0,1915
En consecuencia, el 19,15 % de los diabéticos de esa muestra tiene una glucemia basal
comprendida entre 106 y 110 mg por ml.
O también, la probabilidad de tener una glucemia basal comprendida entre 106 y 110
mg por ml dentro de esa muestra es de un 0,1915.

8. 3.3. La proporción de diabéticos con una glucemia basal mayor de 120 mg por 100 ml.
Datos:
P (X > 120)
Media = = 106
Desviación típica = σ = 8
En este caso tendríamos que tipificar y hacer el mismo procedimiento que en el ejercicio
1, pero como ya sabemos la P que indica los diabéticos con una glucemia basal
inferior o igual a 120 y sabemos que el área total bajo la curva es 1 es resto de
individuos corresponderá a los que tienen una glucemia superior a 120 mg/ml:
La glucemia basal de los diabéticos atendidos en la consulta de
enfermería puede considerarse como una variable normalmente
distribuida con media 106 mg por 100ml y desviación típica de 8 mg
por 100 ml N (106;8)

9. P (X > 120) = P (Z > 1,75) = 1 – P (Z ≤ 1,75) = 1 – 0,9599 = 0,0401
En consecuencia, el 4,01 % de los diabéticos de esa muestra tiene una glucemia superior
a 120 mg.
O también, la probabilidad de tener una glucemia basal superior a 120 mg dentro de esa
muestra es de un 0’0401.
1,75

10. 3.4. El nivel de glucemia basal tal que por debajo de él están el 25% de los diabéticos, es
decir, el primer cuartil.
Ahora debemos calcular el valor de Z. Sabemos que dicho valor tiene que ser negativo
puesto que se encuentra a la izquierda de la campana. Como la campana es
simétrica, calculamos el 0,75 y lo cambio de signo (para que sea 0,25 o primer
cuartil).
La glucemia basal de los diabéticos atendidos en la consulta de
enfermería puede considerarse como una variable normalmente
distribuida con media 106 mg por 100ml y desviación típica de 8 mg
por 100 ml N (106;8)

11. Escojo el valor para Z que se corresponda, aproximadamente, con 0,75. En este caso
escogemos el 0,68.
Cambiándolo de signo sería Z= -0,68.
- 0,68
25%

12. Por último tengemos que despejar X de la fórmula:
Z = (X - ) / σ ; -0,68 = ( X – 106) / 8; X = 100,56
En consecuencia, podemos decir que el 25% de los diabéticos de la muestra estudiada
tienen una glucemia basal de 100,56 mg o menos.

13. FIN