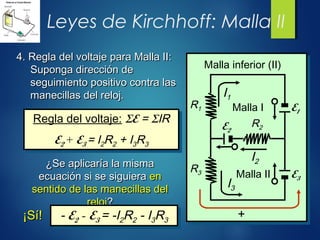
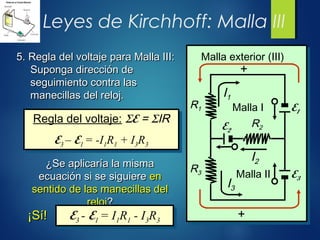
El documento discute los conceptos básicos de circuitos eléctricos, incluyendo símbolos, conexiones en serie y paralelo, y cómo calcular la resistencia equivalente, voltaje y corriente en diferentes configuraciones. Se presentan ejemplos prácticos para ilustrar cómo aplicar la Ley de Ohm y las leyes de Kirchhoff en circuitos simples y complejos. Además, se detallan las convenciones de signos para las fuentes de fuerza electromotriz y las caídas de voltaje en los circuitos.

1. CIRCUITOS
ELÉCTRICOS

2. Símbolos de circuito
eléctrico
Con frecuencia, losCon frecuencia, los circuitos eléctricoscircuitos eléctricos contienencontienen
uno o más resistores agrupados y unidos a unauno o más resistores agrupados y unidos a una
fuente de energía, como una batería.fuente de energía, como una batería.
Los siguientes símbolos se usan conLos siguientes símbolos se usan con
frecuencia:frecuencia:
+ - + -
- + - + -
Tierra Batería
-+
Resistor

3. Resistencias en serie
Se dice que los resistores están conectados enSe dice que los resistores están conectados en
serieserie cuando haycuando hay una sola trayectoriauna sola trayectoria para lapara la
corriente.corriente.
La corrienteLa corriente II es la misma paraes la misma para
cada resistorcada resistor RR11, R, R22 yy RR33..
La energía ganada a través deLa energía ganada a través de EE
se pierde a través dese pierde a través de RR11, R, R22 yy RR33..
Lo mismo es cierto para losLo mismo es cierto para los
voltajes:voltajes:
Para conexiones
en serie:
Para conexiones
en serie:
I = I1 = I2 = I3 VT
= V1 + V2 + V3
I = I1 = I2 = I3 VT
= V1 + V2 + V3
R1
I
VT
R2
R3
Sólo una corriente

4. Resistencia equivalente:
Serie
LaLa resistencia equivalente Rresistencia equivalente Ree de algunosde algunos
resistores conectados en serie es igual a laresistores conectados en serie es igual a la
sumasuma de las resistencias individuales.de las resistencias individuales.
VVTT = V= V11 + V+ V22 + V+ V33 ; (V = IR); (V = IR)
IITTRRee = I= I11RR11+ I+ I22RR22 + I+ I33RR33
Pero. . . IPero. . . ITT = I= I11 = I= I22 = I= I33
Re = R1 + R2 + R3
Re = R1 + R2 + R3
R1
I
VT
R2
R3
Resistencia equivalente

5. Ejemplo 1: Encuentre la resistencia
equivalente Re. ¿Cuál es la corriente I en el
circuito?
2 Ω
12 V
1 Ω3 Ω
Re = R1 + R2 + R3
Re = 3 Ω + 2 Ω + 1 Ω = 6 Ω
Re equivalente = 6 ΩRe equivalente = 6 Ω
La corriente se encuentra a partir de la ley de Ohm:La corriente se encuentra a partir de la ley de Ohm: V = IRV = IRee
12 V
6e
V
I
R
= =
Ω I = 2 AI = 2 A

6. Ejemplo 1 (Cont.): Muestre que las caídas
de voltaje a través de los tres resistores
totaliza la fem de 12 V.
2 Ω
12 V
1 Ω3 Ω
Re = 6 ΩRe = 6 Ω I = 2 AI = 2 A
VV11 = IR= IR11; V; V22 = IR= IR2;2; VV33 = IR= IR33
Corriente I = 2 A igual en cada R.Corriente I = 2 A igual en cada R.
VV11 == (2 A)(1(2 A)(1 Ω) = 2 V
VV11 == (2 A)(2(2 A)(2 Ω) = 4 V
VV11 == (2 A)(3(2 A)(3 Ω) = 6 V
VV11 + V+ V22 + V+ V33 = V= VTT
2 V + 4 V + 6 V = 12 V2 V + 4 V + 6 V = 12 V
¡Compruebe!¡Compruebe!

7. Fuentes de FEM en serie
LaLa dirección de salidadirección de salida de unade una
fuente de fem es desde el ladofuente de fem es desde el lado ++:: E
+-
a b
Por tanto, dePor tanto, de aa aa bb elel potencial aumentapotencial aumenta enen E; de; de
bb aa aa, el, el potencial disminuyepotencial disminuye enen E..
Ejemplo:Ejemplo: EncuentreEncuentre ∆∆VV parapara
la trayectoriala trayectoria ABAB y luego paray luego para
la trayectoriala trayectoria BABA..
R
3 V
+-
+
-
9 V
A
B
AB:AB: ∆∆V = +9 V – 3 V =V = +9 V – 3 V = +6 V+6 V
BA:BA: ∆∆V = +3 V - 9 V =V = +3 V - 9 V = -6 V-6 V

8. Un solo circuito completo
Considere el siguienteConsidere el siguiente circuito en seriecircuito en serie simple:simple:
2 Ω
3 V
+-
+
-
15 V
A
C B
D
4 Ω
Trayectoria ABCD: La
energía y V aumentan a
través de la fuente de 15 V y
disminuye a través de la
fuente de 3 V.
15 V - 3 V = 12 VΣE =
La ganancia neta en potencial se pierde aLa ganancia neta en potencial se pierde a
través de los dos resistores: estas caídas detravés de los dos resistores: estas caídas de
voltaje están envoltaje están en IRIR22 ee IRIR44, de modo que, de modo que la sumala suma
es cero para toda la mallaes cero para toda la malla..

9. Encontrar I en un circuito
simple
2 Ω
3 V
+-
+
-
18 V
A
C B
D
3 Ω
Ejemplo 2:Ejemplo 2: Encuentre la corrienteEncuentre la corriente II en el siguiente circuito:en el siguiente circuito:
18V 3 V 15VΣ − =E =
+ 2 5RΣ Ω Ω = Ω= 3
Al aplicar la ley de Ohm:Al aplicar la ley de Ohm:
15 V
5
I
R
Σ
= =
Σ Ω
E
I = 3 A
En general, para unEn general, para un
circuito de una sola malla:circuito de una sola malla:
I
R
Σ
=
Σ
E

10. Resumen
Circuitos de malla sencilla:
Regla de resistencia: Re = ΣR
Regla de voltaje: ΣE = ΣIR
R2
E1
E2
R1
∑
∑=
R
I:Corriente
ε

11. Circuitos complejos
Un circuitoUn circuito complejocomplejo eses
aquel que contiene másaquel que contiene más
de una malla y diferentesde una malla y diferentes
trayectorias de corriente.trayectorias de corriente.
R2 E1
R3 E2
R1
I1
I3
I2
m nEn los nodos m y n:En los nodos m y n:
II11 = I= I22 + I+ I33 oo II22 + I+ I33 = I= I11
Regla de nodo:
ΣI (entra) = ΣI (sale)
Regla de nodo:
ΣI (entra) = ΣI (sale)

12. Conexiones en paralelo
Se dice que los resistores están conectados enSe dice que los resistores están conectados en paraleloparalelo
cuando hay más de una trayectoria para la corriente.cuando hay más de una trayectoria para la corriente.
2 Ω 4 Ω 6 Ω
Conexión en serie:
Para resistores en serie:Para resistores en serie:
II22 = I= I44 = I= I66 = I= ITT
VV22 + V+ V44 + V+ V66 = V= VTT
Conexión en paralelo:
6 Ω2 Ω 4 Ω
Para resistores enPara resistores en
paralelo:paralelo:
VV22 = V= V44 = V= V66 = V= VTT
II22 + I+ I44 + I+ I66 = I= ITT

13. Resistencia equivalente:
Paralelo
VVTT = V= V11 = V= V22 = V= V33
IITT = I= I11 + I+ I22 + I+ I33
Ley deLey de
Ohm:Ohm:
V
I
R
=
31 2
1 2 3
T
e
VV V V
R R R R
= + +
1 2 3
1 1 1 1
eR R R R
= + +
Resistencia equivalente
para resistores en paralelo:
Resistencia equivalente
para resistores en paralelo: 1
1 1N
ie iR R=
= ∑
Conexión en paralelo:
R3R2
VT
R1

14. Ejemplo 3. Encuentre la resistencia
equivalente Re para los tres resistores
siguientes.
R3R2VT R1
2 Ω 4 Ω 6 Ω1
1 1N
ie iR R=
= ∑
1 2 3
1 1 1 1
eR R R R
= + +
1 1 1 1
0.500 0.250 0.167
2 4 6eR
= + + = + +
Ω Ω Ω
1 1
0.917; 1.09
0.917
e
e
R
R
= = = Ω Re = 1.09 ΩRe = 1.09 Ω
Para resistores en paralelo, Re es menor que la más baja Ri.Para resistores en paralelo, Re es menor que la más baja Ri.

15. Ejemplo 3 (Cont.): Suponga que una fem de
12 V se conecta al circuito que se muestra.
¿Cuál es la corriente total que sale de la
fuente de fem?
R3R2
12 V
R1
2 Ω 4 Ω 6 Ω
VT
VVTT == 12 V;12 V; RRee = 1.09= 1.09 ΩΩ
VV11 = V= V22 = V= V33 = 12= 12 VV
IITT = I= I11 + I+ I22 + I+ I33
Ley de Ohm:Ley de Ohm:
V
I
R
=
12 V
1.09
T
e
e
V
I
R
= =
Ω
Corriente total: IT = 11.0 A

16. Ejemplo 3 (Cont.): Muestre que la corriente
que sale de la fuente IT es la suma de las
corrientes a través de los resistores R1, R2 y
R3.
R3R2
12 V
R1
2 Ω 4 Ω 6 Ω
VT
IITT == 11 A;11 A; RRee = 1.09= 1.09 ΩΩ
VV11 = V= V22 = V= V33 == 12 V12 V
IITT = I= I11 + I+ I22 + I+ I33
1
12 V
6 A
2
I = =
Ω
2
12 V
3 A
4
I = =
Ω
3
12 V
2 A
6
I = =
Ω
6 A + 3 A + 2 A = 11 A6 A + 3 A + 2 A = 11 A ¡Compruebe!¡Compruebe!

17. Combinaciones en serie y en
paralelo
En circuitos complejos, los resistores conEn circuitos complejos, los resistores con
frecuencia se conectanfrecuencia se conectan tanto entanto en serieserie comocomo enen
paraleloparalelo..
VT
R2 R3
R1
En tales casos, es mejor
usar las reglas para
resistencias en serie y en
paralelo para reducir el
circuito a un circuito
simple que contenga una
fuente de fem y una
resistencia equivalente.
En tales casos, es mejor
usar las reglas para
resistencias en serie y en
paralelo para reducir el
circuito a un circuito
simple que contenga una
fuente de fem y una
resistencia equivalente.
VT
Re

18. Ejemplo 4. Encuentre la resistencia
equivalente para el circuito siguiente
(suponga VT = 12 V).
3,6
(3 )(6 )
2
3 6
R
Ω Ω
= = Ω
Ω + Ω
RRee = 4= 4 ΩΩ + 2+ 2 ΩΩ
Re = 6 ΩRe = 6 Ω
VT 3 Ω 6 Ω
4 Ω
12 V 2 Ω
4 Ω
6 Ω12 V

19. Ejemplo 4 (Cont.) Encuentre la corriente total
IT.
VT 3 Ω 6 Ω
4 Ω
12 V 2 Ω
4 Ω
6 Ω12 V
IT
Re = 6 ΩRe = 6 Ω
IT = 2.00 AIT = 2.00 A
12 V
6
T
e
V
I
R
= =
Ω

20. Ejemplo 4 (Cont.) Encuentre las
corrientes y los voltajes a través de cada
resistor.
I4 = IT = 2 AI4 = IT = 2 A
VV44 == (2 A)(4(2 A)(4 ΩΩ) = 8 V) = 8 V
El resto del voltaje (12 V – 8 V =El resto del voltaje (12 V – 8 V = 4 V4 V) cae a) cae a
través detravés de CADA UNOCADA UNO de los resistores paralelos.de los resistores paralelos.
V3 = V6 = 4 VV3 = V6 = 4 V
Esto también se puede encontrar de
V3,6 = I3,6R3,6 = (2 A)(2 Ω)
Esto también se puede encontrar de
V3,6 = I3,6R3,6 = (2 A)(2 Ω)
VT 3 Ω 6 Ω
4 Ω
(Continúa. . .)(Continúa. . .)

21. Ejemplo 4 (Cont.) Encuentre las corrientes y
los voltajes a través de cada resistor.
V6 = V3 = 4 VV6 = V3 = 4 VV4 = 8 VV4 = 8 V
VT 3 Ω 6 Ω
4 Ω
3
3
3
4V
3
V
I
R
= =
Ω I3 = 1.33 AI3 = 1.33 A
6
6
6
4V
6
V
I
R
= =
Ω I6 = 0.667 AI6 = 0.667 A I4 = 2 AI4 = 2 A
Note que laNote que la regla del notoregla del noto se satisface:se satisface:
IT = I4 = I3 + I6
IT = I4 = I3 + I6ΣI (entra) = ΣI (sale)ΣI (entra) = ΣI (sale)

22. Leyes de Kirchhoff para circuitos
CD
Primera ley de Kirchhoff:Primera ley de Kirchhoff: La suma de lasLa suma de las
corrientes que entran a un nodo es igual a lacorrientes que entran a un nodo es igual a la
suma de las corrientes que salen del nodo.suma de las corrientes que salen del nodo.
Primera ley de Kirchhoff:Primera ley de Kirchhoff: La suma de lasLa suma de las
corrientes que entran a un nodo es igual a lacorrientes que entran a un nodo es igual a la
suma de las corrientes que salen del nodo.suma de las corrientes que salen del nodo.
Segunda ley de Kirchhoff:Segunda ley de Kirchhoff: La suma de las fem alrededorLa suma de las fem alrededor
de cualquier malla cerrada debe ser igual a la suma dede cualquier malla cerrada debe ser igual a la suma de
las caídas de IR alrededor de la misma malla.las caídas de IR alrededor de la misma malla.
Segunda ley de Kirchhoff:Segunda ley de Kirchhoff: La suma de las fem alrededorLa suma de las fem alrededor
de cualquier malla cerrada debe ser igual a la suma dede cualquier malla cerrada debe ser igual a la suma de
las caídas de IR alrededor de la misma malla.las caídas de IR alrededor de la misma malla.
Regla del nodo: ΣI (entra) = ΣI (sale)Regla del nodo: ΣI (entra) = ΣI (sale)
Regla de voltaje: ΣE = ΣIRRegla de voltaje: ΣE = ΣIR

23. Convenciones de signos para
fem
 Cuando aplique las leyes de Kirchhoff debe suponerCuando aplique las leyes de Kirchhoff debe suponer
unauna dirección de seguimientodirección de seguimiento positiva y consistente.positiva y consistente.
 Cuando aplique laCuando aplique la regla del voltajeregla del voltaje, las fem son, las fem son
positivaspositivas si la dirección de salida normal de la fem essi la dirección de salida normal de la fem es
enen la dirección de seguimiento supuesta.la dirección de seguimiento supuesta.
 Si el seguimiento es deSi el seguimiento es de A a BA a B,,
esta fem se consideraesta fem se considera positivapositiva..
E
A B
++
 Si el seguimiento es deSi el seguimiento es de B a AB a A,,
esta fem se consideraesta fem se considera negativanegativa..
E
A B
++

24. Signos de caídas IR en circuitos
 Cuando aplique laCuando aplique la regla del voltajeregla del voltaje, las, las caíadas IRcaíadas IR
sonson positivaspositivas si la dirección de corriente supuestasi la dirección de corriente supuesta
eses enen la dirección de seguimiento supuesta.la dirección de seguimiento supuesta.
 Si el seguimiento es deSi el seguimiento es de A aA a
BB, esta caída IR es, esta caída IR es positivapositiva..
 Si el seguimiento es deSi el seguimiento es de B aB a
AA, esta caída IR es, esta caída IR es negativanegativa..
I
A B
++
I
A B
++

25. Leyes de Kirchhoff: Malla I
R3
R1
R2E2
E1
E3
1. Suponga posibles flujos de1. Suponga posibles flujos de
corrientes consistentes.corrientes consistentes.
2. Indique direcciones de salida2. Indique direcciones de salida
positivas para fem.positivas para fem.
3. Indique dirección de3. Indique dirección de
seguimiento consistenteseguimiento consistente
(sentido manecillas del reloj)(sentido manecillas del reloj)
+
Malla I
I1
I2
I3
Regla del nodo: I2 = I1 + I3
Regla del nodo: I2 = I1 + I3
Regla del voltaje: ΣE = ΣIR
E1 + E2 = I1R1 + I2R2
Regla del voltaje: ΣE = ΣIR
E1 + E2 = I1R1 + I2R2

26. Leyes de Kirchhoff: Malla II
4. Regla del voltaje para Malla II:4. Regla del voltaje para Malla II:
Suponga dirección deSuponga dirección de
seguimiento positivo contra lasseguimiento positivo contra las
manecillas del reloj.manecillas del reloj.
Regla del voltaje: ΣE = ΣIR
E2 + E3 = I2R2 + I3R3
Regla del voltaje: ΣE = ΣIR
E2 + E3 = I2R2 + I3R3
R3
R1
R2E2
E1
E3
Malla I
I1
I2
I3
Malla II
Malla inferior (II)
+
¿Se aplicaría la misma¿Se aplicaría la misma
ecuación si se siguieraecuación si se siguiera enen
sentido de las manecillas delsentido de las manecillas del
relojreloj??
- E2 - E3 = -I2R2 - I3R3
- E2 - E3 = -I2R2 - I3R3¡Sí!¡Sí!

27. Leyes de Kirchhoff: Malla III
5. Regla del voltaje para Malla III:5. Regla del voltaje para Malla III:
Suponga dirección deSuponga dirección de
seguimiento contra lasseguimiento contra las
manecillas del reloj.manecillas del reloj.
Regla del voltaje: ΣE = ΣIR
E3 – E1 = -I1R1 + I3R3
Regla del voltaje: ΣE = ΣIR
E3 – E1 = -I1R1 + I3R3
¿Se aplicaría la misma¿Se aplicaría la misma
ecuación si se siguiereecuación si se siguiere enen
sentido de las manecillas delsentido de las manecillas del
relojreloj??
E3 - E1 = I1R1 - I3R3
E3 - E1 = I1R1 - I3R3¡Sí!¡Sí!
R3
R1
R2E2
E1
E3
Malla I
I1
I2
I3
Malla II
Malla exterior (III)
+
+

28. Cuatro ecuaciones
independientes
6. Por tanto, ahora se tienen6. Por tanto, ahora se tienen
cuatro ecuacionescuatro ecuaciones
independientes a partir de lasindependientes a partir de las
leyes de Kirchhoff:leyes de Kirchhoff:
R3
R1
R2E2
E1
E3
Malla I
I1
I2
I3
Malla II
Malla exterior (III)
+
+
II22 = I= I11 + I+ I33
EE11 ++ EE22 = I= I11RR11 + I+ I22RR22
EE22 ++ EE33 = I= I22RR22 + I+ I33RR33
EE33 -- EE11 = -I= -I11RR11 + I+ I33RR33

29. Ejemplo 5. Use las leyes de Kirchhoff
para encontrar las corrientes en el
circuito siguiente.
10 Ω
12 V
6 V
20 Ω
5 Ω
Regla del nodo: I2 + I3 = I1
Regla del nodo: I2 + I3 = I1
12 V = (512 V = (5 ΩΩ))II11 + (10+ (10 ΩΩ))II22
Regla del voltaje:Regla del voltaje: ΣΣEE == ΣΣIRIR
Considere el seguimiento de laConsidere el seguimiento de la
Malla IMalla I en sentido de lasen sentido de las
manecillas del relojmanecillas del reloj para obtener:para obtener:
Al recordar queAl recordar que V/V/ΩΩ = A= A, se obtiene, se obtiene
5I1 + 10I2 = 12 A5I1 + 10I2 = 12 A
I1
I2
I3
+
Malla I

30. Ejemplo 5 (Cont.) Encuentre las
corrientes.
6 V = (206 V = (20 ΩΩ))II33 - (10- (10 ΩΩ))II22
Regla del voltaje:Regla del voltaje: ΣΣEE == ΣΣIRIR
Considere el seguimiento de laConsidere el seguimiento de la
Malla IIMalla II en sentido de lasen sentido de las
manecillas del relojmanecillas del reloj para obtener:para obtener:
10I3 - 5I2 = 3 A10I3 - 5I2 = 3 A
10 Ω
12 V
6 V
20 Ω
5 ΩI1
I2
I3
+
Loop IISimplifique: al dividir entre 2Simplifique: al dividir entre 2
yy V/V/ΩΩ = A= A, se obtiene, se obtiene

31. Ejemplo 5 (Cont.) Tres ecuaciones
independientes se pueden resolver para I1, I2 e
I3.
(3) 10I3 - 5I2 = 3 A(3) 10I3 - 5I2 = 3 A 10 Ω
12 V
6 V
20 Ω
5 ΩI1
I2
I3
+
Malla II
(1) I2 + I3 = I1
(1) I2 + I3 = I1
(2) 5I1 + 10I2 = 12 A(2) 5I1 + 10I2 = 12 A
Sustituya la Ec.Sustituya la Ec. (1)(1) parapara II11 enen (2)(2)::
5(5(II22 + I+ I33) + 10) + 10II33 = 12 A= 12 A
Al simplificar se obtiene:Al simplificar se obtiene:
5I2 + 15I3 = 12 A5I2 + 15I3 = 12 A

32. Ejemplo 5 (Cont.) Se pueden resolver
tres ecuaciones independientes.
(3) 10I3 - 5I2 = 3 A(3) 10I3 - 5I2 = 3 A(1) I2 + I3 = I1
(1) I2 + I3 = I1
(2) 5I1 + 10I2 = 12 A(2) 5I1 + 10I2 = 12 A 15I3 + 5I2 = 12 A15I3 + 5I2 = 12 A
Elimine IElimine I22 al sumar las ecuaciones de la derecha:al sumar las ecuaciones de la derecha:
10I3 - 5I2 = 3 A
15I3 + 5I2 = 12 A
2525II33 == 1515 AA
I3 = 0.600 A
Al poner IAl poner I33 = 0.6 A en (3) produce:= 0.6 A en (3) produce:
10(0.6 A) – 510(0.6 A) – 5II22 = 3= 3 AA
I2 = 0.600 AI2 = 0.600 A
Entonces, de (1):Entonces, de (1): I1 = 1.20 AI1 = 1.20 A