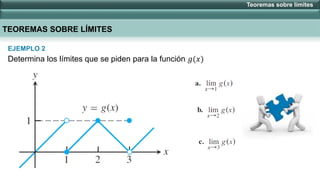
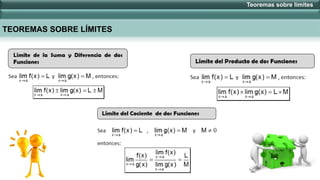
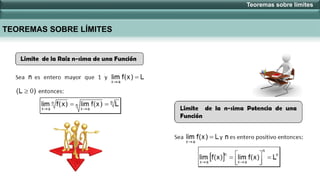
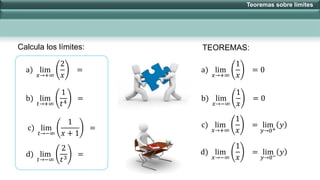
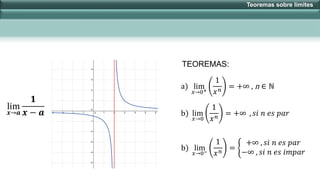
Este documento presenta varios teoremas sobre límites infinitos y límites al infinito. Explica cómo calcular límites cuando x tiende a infinito o cuando x decrece/crece ilimitadamente aplicando dichos teoremas. También cubre cómo calcular límites cuando x se acerca a cero y define los límites como +∞ o -∞ dependiendo de si n es par o impar. Finalmente, incluye ejemplos de aplicación de los teoremas.

1. EJEMPLO 1:
Encuentra los límites que se piden para la función 𝑓(𝑡)
Teoremas sobre límites
TEOREMAS SOBRE LÍMITES

2. EJEMPLO 2
Determina los límites que se piden para la función 𝑔(𝑥)
Teoremas sobre límites
TEOREMAS SOBRE LÍMITES

3. Teoremas sobre límites
TEOREMAS SOBRE LÍMITES

4. Calcula los límites aplicando teoremas:
a) lim
𝑥→−4
8𝑥 +
3𝑥
𝑥 + 1
=
b) lim
𝑢→6
2 −
𝑢
𝑢 − 3
=
c) lim
𝑣→𝜋/2
𝑠𝑒𝑛𝑣 − 2 𝑣𝑐𝑠𝑐𝑣 =
d) lim
𝑡→ 3
3𝑡 − 1
𝑡 − 1
=
Teoremas sobre límites
TEOREMAS SOBRE LÍMITES
EJEMPLO 2

5. Teoremas sobre límites
TEOREMAS SOBRE LÍMITES

6. EJEMPLOS
a) lim
𝑥→3
𝑥 − 2 =
b) lim
𝑡→6
0,75 −
𝑡
5
=
c) lim
𝑣→𝜋/2
𝜋 +
2
𝑣
=
d) lim
𝑢→1/3
= 𝑢 +
1
𝑢
=
Calcula los límites aplicando teoremas:
Teoremas sobre límites
TEOREMAS SOBRE LÍMITES

7. Teoremas sobre límites
TEOREMAS SOBRE LÍMITES

8. a) lim
𝑥→1
𝑥3 − 3𝑥2 + 0,3𝑥7 =
b) lim
𝑢→2
𝑢 + 7 =
c) lim
𝑣→2
6
𝑣4 + 16𝑣 =
d) lim
𝑡→ 𝜋
𝑡4
− 2𝑡 =
Calcula los límites aplicando teoremas:
Teoremas sobre límites
TEOREMAS SOBRE LÍMITES
EJEMPLOS

10. 𝐥𝐢𝐦
𝒙→+∞
𝒇 𝒙 = 𝒃 ↔ ∀𝜺 > 𝟎; ∃ 𝑲 ∈ ℝ/𝒙 ∈ Dom(f ) ∧ 𝒙 < 𝑲 → 𝒇 𝒙 − 𝒃 < 𝜺
❑ Un número real “ 𝑏” se dice que es el límite de 𝑓(𝑥)
cuando𝑥tiende a +∞ o cuando 𝑥crece ilimitadamente
❑ Un número real “ 𝑏 ” se dice que es el límite de 𝑓(𝑥)
cuando𝑥tiende a −∞ o cuando 𝑥 decrece ilimitadamente
𝐥𝐢𝐦
𝒙→−∞
𝒇 𝒙 = 𝒃 ↔ ∀𝜺 > 𝟎; ∃ 𝑲 ∈ ℝ/𝒙 ∈ Dom(f ) ∧ 𝒙 < 𝑲 → 𝒇 𝒙 − 𝒃 < 𝜺
LÍMITES INFINITOS Y LÍMITES AL INFINITO

11. a) lim
𝑥→+∞
2
𝑥
=
b) lim
𝑡→+∞
1
𝑡4
=
Calcula los límites:
c) lim
𝑡→−∞
1
𝑥 + 1
=
d) lim
𝑡→−∞
2
𝑡3
=
TEOREMAS:
a) lim
𝑥→+∞
1
𝑥
= 0
b) lim
𝑥→−∞
1
𝑥
= 0
c) lim
𝑥→+∞
1
𝑥
= lim
𝑦→0+
𝑦
d) lim
𝑥→−∞
1
𝑥
= lim
𝑦→0−
𝑦
Teoremas sobre límites

12. lim
𝒙→𝒂
𝟏
𝒙 − 𝒂
TEOREMAS:
a) lim
𝑥→0+
1
𝑥 𝑛
= +∞ , n ∈ ℕ
b) lim
𝑥→0
1
𝑥 𝑛
= +∞ , 𝑠𝑖 𝑛 𝑒𝑠 𝑝𝑎𝑟
b) lim
𝑥→0−
1
𝑥 𝑛
= ቊ
+∞ , 𝑠𝑖 𝑛 𝑒𝑠 𝑝𝑎𝑟
−∞ , 𝑠𝑖 𝑛 𝑒𝑠 𝑖𝑚𝑝𝑎𝑟
Teoremas sobre límites

13. TEOREMAS:LÍMITES AL INFINITO
a) lim
𝑥→+∞
1
𝑥
= 0
b) lim
𝑥→−∞
1
𝑥
= 0
c) lim
𝑥→+∞
1
𝑥
= lim
𝑦→0+
𝑦
d) lim
𝑥→−∞
1
𝑥
= lim
𝑦→0−
𝑦
TEOREMAS: LÍMITES INFINITOS
a) lim
𝑥→0+
1
𝑥 𝑛
= +∞ , n ∈ ℕ
b) lim
𝑥→0
1
𝑥 𝑛
= +∞ , 𝑠𝑖 𝑛 𝑒𝑠 𝑝𝑎𝑟
b) lim
𝑥→0−
1
𝑥 𝑛
= ቊ
+∞ , 𝑠𝑖 𝑛 𝑒𝑠 𝑝𝑎𝑟
−∞ , 𝑠𝑖 𝑛 𝑒𝑠 𝑖𝑚𝑝𝑎𝑟
TEOREMAS SOBRE LÍMITES