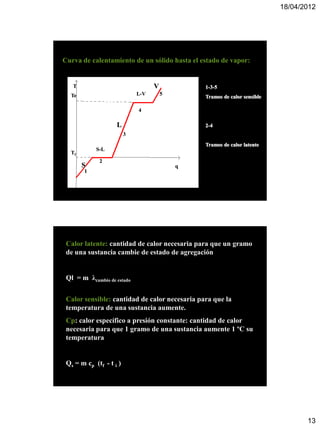
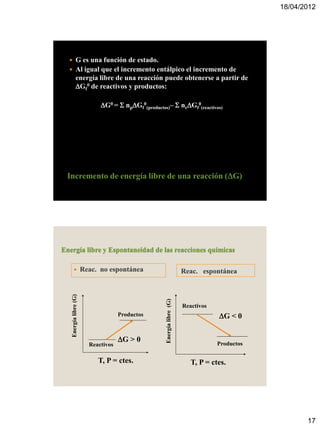
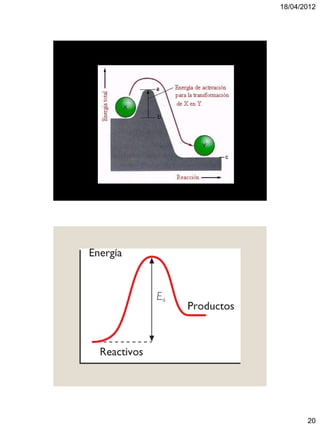
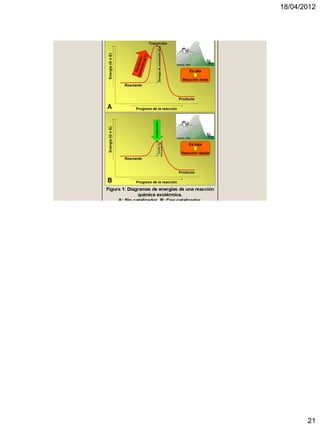
El documento trata sobre termoquímica. Explica que la termoquímica estudia el intercambio energético de sistemas químicos con el exterior. Define conceptos como sistemas abiertos, cerrados y aislados, y reacciones exotérmicas y endotérmicas. También introduce variables de estado, funciones de estado, calor, temperatura y energía interna.

1. 18/04/2012
Termoquímica
Termoquímica:
Es la parte de la Química que se
encarga del estudio del intercambio
energético de un sistema químico con
el exterior.
1

2. 18/04/2012
Sistema:
Parte pequeña del universo que se aísla para
someter a estudio.
El resto se denomina Entorno.
Pueden ser:
Abiertos (intercambia materia
y energía).
Cerrados (no intercambia materia
y sí energía).
Aislados (no intercambia ni materia
ni energía).
Hay sistemas químicos que evolucionan de
reactivos a productos desprendiendo energía.
Son las reacciones exotérmicas.
Otros sistemas químicos evolucionan de
reactivos a productos precisando energía.
Son las reacciones endotérmicas.
2

3. 18/04/2012
Variables de estado
Magnitudes que pueden variar a lo largo de un
proceso (por ejemplo, en el transcurso de una
reacción química) .
Ejemplos: Presión, Temperatura, Volumen,
Concentración.
Funciones de Estado
Tienen un valor único para cada estado del
sistema.
Su variación solo depende del estado inicial y
final y no del camino desarrollado.
SÍ son: Presión, temperatura, energía interna,
entalpía.
NO son: calor, trabajo
3

4. 18/04/2012
Calor
El calor es energía transferida entre dos cuerpos o
sistemas. Representa la energía total del
movimiento molecular
El joule (J) es la unidad de energía del SI
Temperatura
Es una magnitud escalar relacionada con la
energía interna de un sistema termodinámico
La temperatura es una medida de la energía
molecular media.
En el SI, la unidad de temperatura es el grado
Kelvin
Energía interna (U)
Es la energía total el sistema.
Es imposible medir.
Su variación sí se mide.
U=Q+W
U es función de estado.
Q: calor
W: trabajo ( fundamentalmente expansivo ; W = P  V
P = presión ;  V= variación de volumen
4

5. 18/04/2012
Primer principio de la Termodinámica
CALOR CALOR
Q>0 U=Q+W Q<0
TRABAJO TRABAJO
W< 0 W>0
U=Q+W
Calor a volumen constante:
Es el intercambio de energía en un recipiente
cerrado que no cambia de volumen.
Si V= constante, es decir, V = 0
W= PV = 0 
Qv = U
5

6. 18/04/2012
Calor a presión constante
La mayoría de los procesos químicos ocurren a presión
constante, normalmente la atmosférica.
Si P = cte  W = – P ·  V
 U = Qp – P ·  V
U2 – U1 = Qp – P · (V2 – V1)
Qp + U1 + P· V1 = U2 + P · V2
H1 H2
H es función de estado
Qp = H2 – H1 =  H (entalpía)
H1= U1 + P · V1  Qp = H 2 – H1 =  H
H2= U2 + P · V2
Qp + H 1 = H 2
H es una función de estado.
Reac. endotérmica
Reac. endotérmica Reac. exotérmica
Productos Reactivos
Entalpia (H)
Productos
H < 0
Entalpia (H)
H > 0
Entalpia (H)
Reactivos
H > 0
Reactivos Productos
6

7. 18/04/2012
Calor molar de formación:
Entalpía de formación
Es la variación de entalpía (H) que se produce en la reacción
de formación de un mol de un determinado compuesto a partir
de los elementos en estado físico normal (más abundante).
Cuando se lo mide a 25ºC y 1 atm de Presión se lo denomina
calor standard
Se expresa como Hfº. Se mide en kJ/mol.
Ejemplos:
C (s) + O2 (g)  CO2 (g) Hf º = – 393,13 kJ/mol
H2 (g) + ½ O 2(g)  H2O (l) Hf º = – 285,8 kJ/mol
Recuerda
Hfº de todos los elementos en estado original es 0.
7

8. 18/04/2012
Calor de reacción:
Es la variación de entalpía de una reacción y se calcula:
Hr = ∑ np  Hproductos – ∑ nr  Hreactivos
Cuando, tanto reactivos como productos están en condiciones
estándar (P = 1 atm; T = 298 K = 25 ºC).
Se expresa como Hº, se mide en J o kJ depende de cómo se
ajuste la reacción.
O sea que el calor de formación es un caso particular de calor
de reacción
Ecuaciones termoquímicas:
Expresan tanto los reactivos como los productos indicando entre
paréntesis su estado físico, y a continuación la variación
energética expresada como H (habitualmente como Hº).
Ejemplos:
H 2(g) + ½ O 2(g)  H2O (g) Hº = –241,4 kJ/mol
H2 (g) + ½ O2 (g)  H2O(l) Hº= – 285,8 kJ/mol
Por lo tanto
H2O (l) H 2O (g) Hº= 44,4 kJ
8

9. 18/04/2012
Ejemplos:
H 2(g) + ½ O 2(g)  H2O (g) Hºf = –241,4 kJ/mol
H 2 (g) + ½ O2 (g)  H2O(l) Hºf= – 285,8 kJ/mol
Por lo tanto para
H2O (l) H 2O (g)
si
Hr = ∑ Hproductos – ∑ Hreactivos
Hcambio de estado liq a vapor = -241,4 – (-285,8) = 44,4 kJ
H2O (l) H 2O (g) Hvº= 44,4 kJ
Importante:
El Hºr
2 H2 (g) + O2 (g)  2 H2O (l) Hºr – 571,6 kJ
es el doble del de
H2 (g) + ½ O2 (g)  H2O(l) Hºr – 285,8 kJ
9

10. 18/04/2012
CH4(g) + 2 O2(g)  CO2(g) + 2 H2O(l) Hº = –890 kJ
Hr = ∑ np  Hproductos – ∑ nr  Hreactivos
Hr = (2 Hºf H2O + Hºf CO2) – (Hºf CH4)
 Hproductos <  Hreactivos  reacción exotérmica
Calor de combustión:
Cantidad de calor liberada al quemar un mol de un compuesto en
presencia de oxígeno gaseoso, para obtener fundamentalmente
dióxido de carbono gaseoso y agua líquida
Calor de disolución:
Calor puesto en juego al disolver 1 mol de un compuesto en un
solvente dado
Calor de neutralización:
Calor puesto en juego al neutralizar 1 mol de un ácido con una base
o viceversa
Calor de cambio de estado:
Cantidad de calor puesta en juego al ( fundir, solidificar,
condensar…..) 1 mol de una sustancia
10

11. 18/04/2012
Ejemplo: Conocidas las entalpías estándar de formación
del butano (C4H10), agua líquida y CO2, cuyos valores son
respectivamente –124,7, –285,8 y –393,5 kJ/mol, calcular la
entalpía estándar de combustión del butano.
La reacción de combustión del butano es:
C4H10(g) +13/2O2(g)  4 CO2(g) + 5H2O (l) Hºcomb = ?
Hº =  npHfº(product.) –  nrHfº(reactivos)
= 4 mol(– 393,5 kJ/mol) + 5 mol(– 285,8 kJ/mol)
–1 mol(– 124,7 kJ/mol) = – 2878,3 kJ
Luego la entalpía estándar de combustión será:
 Hºcombustión = – 2878,3 kJ/mol
LEY Termoquímicas
Ley de Hess:
La entalpía en una reacción química es constante con
independencia de que la reacción se produzca en una o más
etapas. Como la H es función de estado, si una ecuación
química se puede expresar como combinación lineal de otras,
podremos igualmente calcular H de la reacción global
combinando los H de cada una de las reacciones.
Ley de Lavoisier:
La variación de entapía de la reacción directa es
numéricamente igual al de la reacción inversa pero con el signo
contrario
11

12. 18/04/2012
Esquema de la ley de Hess
H2(g) + ½ O2(g)
H
H 0 = – 241,8 kJ
D bv 1
H20 = – 285,8 kJ H2O(g)
H30 = 44 kJ
H2O(l)
C4H10(g) +13/2 O2(g)  4 CO2(g) + 5 H2O (l)
Hº = – 2878,3 kJ/mol
4 CO2(g) + 5 H2O (l)  C4H10(g) + 13/2 O2(g)
Hº= + 2878,3 kJ/mol
12

13. 18/04/2012
Curva de calentamiento de un sólido hasta el estado de vapor:
T V 1-3-5
Te L-V 5
Tramos de calor sensible
4
L 2-4
3
Tramos de calor latente
S-L
Tf
2
S q
1
Calor latente: cantidad de calor necesaria para que un gramo
de una sustancia cambie de estado de agregación
Ql = m λcambio de estado
Calor sensible: cantidad de calor necesaria para que la
temperatura de una sustancia aumente.
Cp: calor específico a presión constante: cantidad de calor
necesaria para que 1 gramo de una sustancia aumente 1 ºC su
temperatura
Qs = m cp (tf - t i )
13

14. 18/04/2012
Entropía (S)
 Es una medida del desorden del sistema que sí puede
medirse y tabularse.
S = Sfinal – Sinicial
 Existen tablas de S0 (entropía molar estándar) de diferentes
sustancias.
 En una reacción química:
S0 =  np· S0productos –  nr· S0reactivos
 La entropía es una función de estado.
Ejemplo: Calcula S0 para las siguientes reacciones químicas:
a) N2(g) + O2(g)  2 NO(g);
b) 3 H2(g) + N2(g)  2 NH3(g).
Datos: S0 (J·mol–1·K–1): H2(g) = 130,6; O2(g) =205; N2(g) = 191,5;
NO(g) = 210,7; NH3(g) =192,3
S0 =  np· S0productos –  nr· S0reactivos
a) S0 = 2 mol · 210,7 J ·mol–1 ·K–1 –
(191,5 J·K–1 + 205 J·K–1 ) = 24,9 J·K–1
b) S0 = 2·192,3 J·K–1 –
(3 mol ·130,6 J· mol–1·K–1 + 191,5 J·K–1 ) = –198,7 J·K–1
14

15. 18/04/2012
 “En cualquier proceso espontáneo la entropía
total del universo tiende a aumentar siempre”.
 Suniverso = Ssistema + Sentorno  0
 A veces el sistema pierde entropía (se ordena)
espontáneamente. En dichos casos el entorno se
desordena.
Segundo principio de la Termodinámica.
 “La entropía de cualquier sustancia a 0 K es igual a 0”
(máximo orden).
 Equivale a decir que no se puede bajar de dicha temperatura.
 ¡CUIDADO! Las S de los elementos en condiciones estándar
no son 0 sino que es positiva.
Tercer principio de la Termodinámica
15

16. 18/04/2012
 En procesos reversibles y a temperatura constante se puede calcular
S de un sistema como:
S = Q—T
 y si el proceso químico se produce a presión constante:
 Hsistema
Ssistema = ——— ; – Hsistema
Sentorno= ————
T T
 S0 (entropía molar estándar) se mide en
J·mol–1·K–1.
 Sreacción se mide en J·K–1.
Energía libre de Gibbs (G)
 En procesos a T constante se define como:
G=H–T·S G =  H – T · S
 En condiciones estándar: G0 = H0 – T· S0
 Suniverso = Ssistema + Sentorno > 0 (p. espontáneos)
Multiplicando por “–T” y como “–T Sentorno = Hsist
 –T · Suniverso = – T · Ssist + Hsist = G < 0
 En procesos espontáneos: G < 0
 Si G. > 0 la reacción no es espontánea
 Si G. = 0 el sistema está en equilibrio
16

17. 18/04/2012
 G es una función de estado.
 Al igual que el incremento entálpico el incremento de
energía libre de una reacción puede obtenerse a partir de
Gf0 de reactivos y productos:
G0 =  npGf0(productos)–  nrGf0(reactivos)
Incremento de energía libre de una reacción (G)
Energía libre y Espontaneidad de las reacciones químicas
 Reac. no espontánea Reac. espontánea
Energía libre (G)
Energía libre (G)
Reactivos
Productos G < 0
G > 0 Productos
Reactivos
T, P = ctes. T, P = ctes.
17

18. 18/04/2012
 No siempre las reacciones exotérmicas son espontáneas.
 Hay reacciones endotérmicas espontáneas:
◦ Evaporación de líquidos.
◦ Disolución de sales...
Ejemplos de reacciones endotérmicas espontáneas:
 NH4Cl(s)  NH4+(aq) + Cl– (aq)  H0 = 14,7 kJ
 H2O(l)  H2O(g) H0 = 44,0 kJ
Espontaneidad en las reacciones químicas
Espontaneidad de las reacciones químicas
Una reacción es espontánea cuando
G (H – T x S) es negativo
Según sean positivos o negativos los valores de H y S (T
siempre es positiva) se cumplirá que:
  H < 0 y  S > 0  G < 0 Espontánea
  H > 0 y  S < 0  G > 0 No espontánea
  H < 0 y  S < 0  G < 0 a T bajas
 G > 0 a T altas
  H > 0 y  S > 0  G < 0 a T altas
 G > 0 a T bajas
18

19. 18/04/2012
Espontaneidad de las reacciones químicas
H < 0 S H > 0
S > 0 S > 0
Espontánea a todas Espontánea por
las temperaturas encima de una T
H > 0 H
H < 0
S < 0 S < 0
Espontánea por No Espontánea a
debajo de una T cualquier temperaturas
Ejemplo: ¿Será o no espontánea la siguiente reacción
2H2O2(l) 2H2O (l) + O2(g)
en condiciones estándar? Datos: H0f (kJ/mol) H2O(l) = –285,8; H2O2(l) = –
187,8 ; S0 (J·mol 1 K·1) H2O(l) = 69,9; H2O2(l) = 109,6; O2(g) =205,0.
 H0 =  npHf0(productos)–  nrHf0(reactivos) =
= 2 Hf0(H2O) + Hf0(O2) – 2 Hf0(H2O2) =
2 mol(–285,8 kJ/mol) – 2 mol(–187,8 kJ/mol) = –196,0 kJ
S0 =  np· S0productos –  nr· S0reactivos =
2 S0(H2O) + S0(O2) – 2 S0(H2O2) =
2 mol(69,9 J/mol·K) + 1 mol(205, J/mol·K)
– 2mol(109,6 J/mol·K) = 126,0 J / K = 0,126 kJ / K
G0 =  H0 – T ·  S0 = –196,0 kJ – 298 K · 0,126 kJ/ K =
G0 = – 233,5 kJ luego será espontánea
19

20. 18/04/2012
20

21. 18/04/2012
21