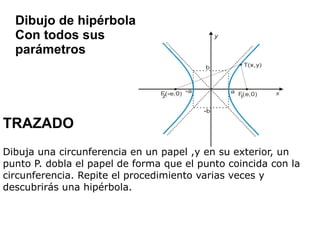
Este documento resume las secciones cónicas más importantes: la elipse, la hipérbola y la parábola. Define cada una en términos de sus parámetros y focos. Explica cómo trazar cada curva manualmente y a través de fórmulas analíticas. Además, proporciona ejemplos comunes de cada sección cónica en la naturaleza y la ingeniería.

1. TRABAJO DE CÓNICAS Carolina Herrera Silvia Cid Pavón Pablo Ernst Sastre 1º Bach CCNN Fecha de entrega: 2- dic.-10

2. INDICE Secciones cónicas de un cono

3. Elipse

4. Hipérbola

5. Parábola

6. Hoja del visionado

7. Opinión personal

8. Secciones cónicas

9. ELIPSE DEFINICIÓN Es el lugar geométrico de los puntos del plano cuya suma de las distancias a dos puntos fijos, llamados focos, es constante. PARAMETROS DE LA ELIPSE 2a=eje mayor AB 2b=eje menor CD 2c=distancia focal FF Los tres parámetros configuran un triangulo rectángulo por lo que se cumple: a2=b2+c2

10. ELIPSE DEFINICIÓN Es el lugar geométrico de los puntos del plano cuya suma de las distancias a dos puntos fijos, llamados focos, es constante. PARAMETROS DE LA ELIPSE 2a=eje mayor AB 2b=eje menor CD 2c=distancia focal FF Los tres parámetros configuran un triangulo rectángulo por lo que se cumple: a2=b2+c2

11. Dibujo de la elipse con los parámetros:

12. TRAZADO Método del jardinero: Para trazar elipses de grandes dimensiones podemos usar una cuerda de longitud igual al eje mayor , colocamos sus extremos sobre los focos y estiramos la cuerda para dibujar la curva . ESTUDIO ANALÍTICO x2/a2 + y2/b2 = 1 Con la formula reducida de la elipse podemos conocer las coordenadas de todos sus puntos.

13. EJEMPLOS REALES -> Órbitas planetarias -> Formas circulares -> Bóvedas elipsoidales -> Iluminación -> Diseño Formas circulares ← Formas gráficas

14. HIPÉRBOLA DEFINICIÓN La hipérbola es el lugar geométrico de los puntos tal que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos , es constante. PARAMETROS DE LAS HIPÉRBOLAS: 2a=eje real V_1V_2 2b=eje virtual 2c=distancia focal FF Los tres parámetros configuran un triangulo rectángulo por lo que se cumple: a2=b2+c2

15. Dibujo de hipérbola Con todos sus parámetros TRAZADO Dibuja una circunferencia en un papel ,y en su exterior, un punto P. dobla el papel de forma que el punto coincida con la circunferencia. Repite el procedimiento varias veces y descubrirás una hipérbola.

16. EJEMPLOS REALES -> Iluminación -> Reloj solar -> LORAN, navegación hiperbólica -> Telescopios de tipo classegrain luminación I ← Reloj solar ESTUDIO ANALITICO Formula x2/a2 - y2/b2 = 1