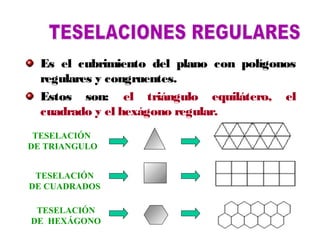
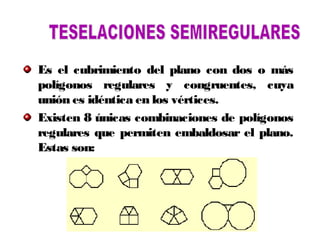
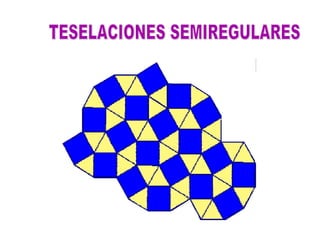
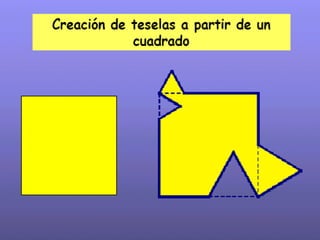
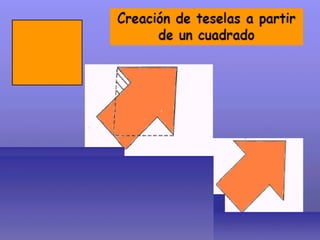
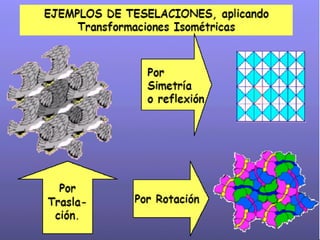
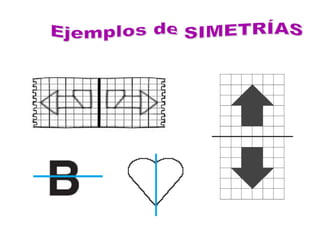
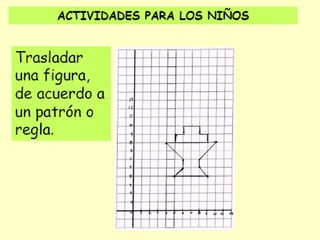
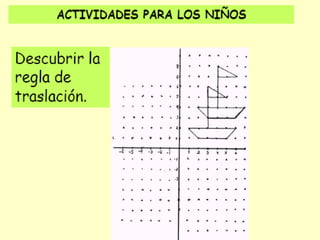
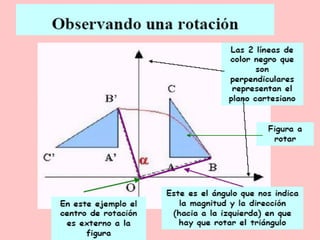
El documento describe las transformaciones isométricas, que son movimientos que mantienen la forma y tamaño de una figura geométrica. Explica los tipos de transformaciones isométricas como simetrías, traslaciones, giros o rotaciones, teselaciones y embaldosamientos. También describe los principios de las isometrías y define la teselación como el cubrimiento del plano con figuras que se repiten sin superponerse.

2. Son movimientos que pueden realizarse con un
figura geométrica, a la cual se le mantiene su
forma y tamaño.
Existen tipos de transformaciones isométricas:
SIMETRÍASIMETRÍA
TRASLACIONESTRASLACIONES
GIROS O ROTACIONESGIROS O ROTACIONES
TESELACIONESTESELACIONES
OO
EMBALDOSAMIENTOSEMBALDOSAMIENTOS

3. Cumplen con 4 principios:
 PRINCIPIODE IDENTIDAD:PRINCIPIODE IDENTIDAD: no altera el objeto.no altera el objeto.
 PRINCIPIODE COMPOSICIÓN:PRINCIPIODE COMPOSICIÓN:
del producto de dos isometrías surge una nueva isometría.del producto de dos isometrías surge una nueva isometría.
PRINCIPIODE ORDEN:PRINCIPIODE ORDEN:
el orden de las composiciones de isometría no alteran alel orden de las composiciones de isometría no alteran al
objeto.objeto.
 PRINCIPIODE INVERSA DE UNA ISOMETRÍA:PRINCIPIODE INVERSA DE UNA ISOMETRÍA:
si existe una isometría, también existe otra isometría quesi existe una isometría, también existe otra isometría que
puede deshaceraquella.puede deshaceraquella.

4. Consiste en recubrir el plano con figuras que se repiten,
de modo que:
 Al unirlas figuras se recubre completamente el plano.
 La intersección de dos figuras es vacía.(no se
superponen)
La figura con la que se realiza la teselación se llama
TESELA.
Tipos de teselaciones: REGULARES,
SEMIREGULARES e IRREGULARES.
Act. 1

5. ReflexionemosReflexionemos
……
• ¿Qué polígonos regulares nos permiten cubrir el plano,
siguiendo las reglas de una teselación?
• ¿Qué otras teselas podemos originar a partir de la
unión de polígonos regulares?
• ¿Cómo podemos generar una nueva tesela, a través de
quitar y agregar partes a una tesela ya definida como
tal?
• ¿Qué aplicaciones prácticas le ven a esta
transformación?

6. Es el cubrimiento del plano con polígonos
regulares y congruentes.
Estos son: el triángulo equilátero, el
cuadrado y el hexágono regular.
TESELACIÓN
DE TRIANGULO
TESELACIÓN
DE CUADRADOS
TESELACIÓN
DE HEXÁGONO

7. Es el cubrimiento del plano con dos o más
polígonos regulares y congruentes, cuya
unión es idéntica en los vértices.
Existen 8 únicas combinaciones de polígonos
regulares que permiten embaldosar el plano.
Estas son:

9. Es el cubrimiento del plano con figuras que
no siguen formas regulares, sino que
representan animales, caras, etc.
Cumplen con el principio “quito-pongo”.

16. Maurits Cornelis Escher, arquitecto,

17. Maurits Cornelis
Escher

18. Maurits Cornelis Escher, arquitecto,
1898

19. Es una isometría fijada por una recta, llamado eje de
reflexión o eje de simetría, cuyos puntos están
equidistantes de ella.
Significa “algo bien proporcionado, equilibrado.”
Son dos subregiones congruentes que en conjunto
forman una región, las cuales son divididas por el eje de
simetría.
Existen tres tipos de simetría:
SIMETRÍA PORREFLEXIÓNSIMETRÍA PORREFLEXIÓN
SIMETRÍA PORTRASLACIÓNSIMETRÍA PORTRASLACIÓN
SIMETRÍA PORROTACIÓNSIMETRÍA PORROTACIÓN
Act. 2, 3 y 4

20. ReflexionemosReflexionemos
……
• ¿Qué sucede con los espejos?
• ¿En qué cosas de la naturaleza encontramos simetría?
• ¿Qué instrumentos necesitamos para dibujar una
figura simétrica?

22. Es el movimiento de una figura en el plano, con una
dirección determinada y una magnitud dada por la
distancia entre el punto de partida y el punto de llegada.
“Es el recorrido que realiza una figura determinado por
un vector”
Act. 5
Es un símbolo que nos indicaEs un símbolo que nos indica
un punto de partida, unaun punto de partida, una
dirección y un punto dedirección y un punto de
llegada en línea recta. (Nosllegada en línea recta. (Nos
indica la distancia y el sentidoindica la distancia y el sentido
en que debe trasladarse laen que debe trasladarse la
figura)figura)

25. Es un giro en torno a:
 un punto determinado de la figura o fuera de ella, el
cual se llama centro de rotación.
 con cierta magnitud, la cual se llama ángulo de
rotación. Esta amplitud se mide en grados.
Act. 6

27. ReflexionemosReflexionemos
……
• ¿A cuántos grados equivale:
… un giro completo?
… un cuarto de giro?
… un medio giro?
… tres cuartos de giro?
Respuesta: 360° , 90° , 180° , 270°,
respectivamente.