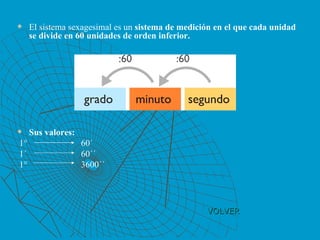
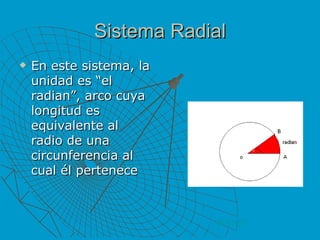
El documento presenta información sobre diferentes sistemas de medición de ángulos (sexagesimal, circular y radial), funciones trigonométricas (seno, coseno y tangente), y reducción de ángulos al tercer cuadrante. Explica las características y propiedades de cada sistema y función, incluyendo dominios, períodos de repetición, valores máximos y mínimos.

1. Sistemas de Medición Funciones seno, coseno, tangente Reducción al tercer cuadrante. SIGUIENTE

2. MENÚ DE SELECCIÓN SISTEMAS DE MEDICIÓN. FUNCIONES: SENO COSENO TANGENTE. REDUCCIÓN AL 3er CUADRANTE. VOLVER

3. VOLVER SISTEMA SEXAGESIMAL SISTEMA CIRCULAR SISTEMA RADIAL Sist. Circular al Sist. Sexagesimal Sist. Sexagesimal al Sist. Circular

4. Sist. Circular al Sist. sexagesimal Una vez dado un ángulo en el Sist. Circular, se necesitan multiplicar las medidas por 180°/ π para que el mismo esté expresado en grados sexagesimales. Ej: 3/5π . 180°/π= 108° VOLVER

5. VOLVER Una vez dado un ángulo en el Sist. Sexagesimal, se necesita multiplicar las medidas por π/180° para que el mismo esté expresado en el Sist. Circular. Ej.: 36° . π/180°= π/5 rad. 36° . π/180°= 0.628 rad. 36°= π/5 rad= 0.628. Sist. Sexagesimal al Sist. Circular

6. VOLVER El sistema sexagesimal es un sistema de medición en el que cada unidad se divide en 60 unidades de orden inferior. Sus valores: 1° 60´ 1´ 60´´ 1° 3600´´

7. VOLVER Este sistema se centra en la medición de ángulos basados en la medida del arco. En este sistema, cuya unidad es el radian, la magnitud viene dada por la medida del arco en un circulo de radio unidad. Una vuelta completa equivale a 2π radianes. Para un ángulo llano π radianes, para un ángulo recto π/2 radianes, etc. Toda una vuelta a la circunferencia es igual a 360° o lo que es lo mismo 2π. 1 giro= 360°= 2π VOLVER

8. Sistema Radial En este sistema, la unidad es “el radian”, arco cuya longitud es equivalente al radio de una circunferencia al cual él pertenece VOLVER

9. FUNCIÓN SENO La función Seno alcanza su valor máximo en: x = π/2 y = 1 Y, su valor mínimo x = 3/2π y = -1 VOLVER sin( θ ) = Opuesto / Hipotenusa

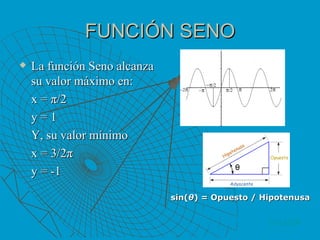
10. Características del Seno. Su dominio contiene a todos los reales. En cambio, su imagen es el intervalo [-1,1], ya que el seno de un ángulo siempre se encuentra entre estos valores. Esta función se repite exactamente igual cada 2π; es decir, los valores de la función en el intervalo del dominio [0,2π) son suficientes para conocer la función en cualquier punto. Se dice, en este caso, que la función es periódica, de período 2π. La función se anula en los valores x iguales a k π, siendo k un número entero. La función alcanza sus extremos máximos, es decir, los valores mayores de la y , cuando el seno del ángulo es 1, es decir, cuando la x es π 2 + 2 kπ , siendo k un número entero cualquiera. Sus extremos mínimos, es decir, los valores menores de la y (cuando el seno es -1), se encuentran cuando la x es 3 π 2 + 2 k π , siendo k cualquier número entero. VOLVER

11. FUNCIÓN COSENO La función coseno alcanza su valor máximo en: x = 0 y = 1 Y, su valor mínimo: x = π y = 1 VOLVER cos( θ ) = Adyacente / Hipotenusa

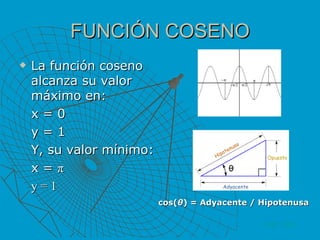
12. Características del Coseno. Su dominio contiene a todos los reales. En cambio, su imagen es el intervalo [-1,1], ya que el coseno de un ángulo siempre se encuentra entre estos valores. Esta función se repite exactamente igual cada 2π; es decir, los valores de la función en el intervalo del dominio [0,2π) son suficientes para conocer la función en cualquier punto. Así pues, es periódica, de período 2π. La función se anula en π 2 + k π, siendo k cualquier número entero. La función alcanza sus extremos máximos, es decir, los valores mayores de la y , cuando el coseno del ángulo es 1, es decir, cuando la x es 2 kπ, siendo k un número entero cualquiera. Sus extremos mínimos, es decir, los valores menores de la y (cuando el seno es -1), se encuentran cuando la x es π + 2 k π, siendo k cualquier número entero. VOLVER cos( θ ) = Adyacente / Hipotenusa

13. Función Tangente Gráfico

14. Características de la Tangente Dominio : R- { (2k+1). π /2, K e Z } = R – {…, - π /2, π /2, 3 π /2, …} Recorrido : R Continuidad : Continua en Ax e R – { ( π /2 + π . K) } Período : π rad. Cortes con el eje OX: X = { 0 + π . K} Impar: tg (-x) = tg x Creciente en: R Máximos : No tiene. Mínimos : No tiene.

15. Reducción al 3er Cuadrante Dado que en el tercer cuadrante las funciones básicas (de las que se derivan todas las demás) seno y coseno son negativas, par π< x < 3/2 π, se tiene sen x : negativo cos x : negativo . . . . . . sen x. . .negativo tan x = ──── = ────── = positivo . . . . . . cos x. . .negativo . . . . . . cos x. . .negativo ctg x = ──── = ────── = positivo . . . . . . sen x. . .negativo sec x = 1 / cos x = 1 / negativo = negativo csc x = 1 / sen x = 1 / negativo = negativo VOLVER + - - III TG COS SEN C °