Este documento describe dos sistemas para medir ángulos: el sistema sexagesimal y el sistema de radianes. Explica las equivalencias entre los sistemas y define las razones trigonométricas de un ángulo agudo, incluyendo seno, coseno, tangente y más. También cubre cómo resolver triángulos rectángulos usando las razones trigonométricas y el teorema de Pitágoras.

1. TRIGONOMETRÍA
SISTEMAS DE MEDIDAS DE ÁNGULOS
Para medir ángulos se utilizan:
1.− Sistema sexagesimal:
La unidad de medida en este sistema es el grado sexagesimal
Un ángulo mide un grado sexagesimal (10) si su arco central correspondiente, es la trescientas
sesentava parte de la circunferencia.
Por tanto:
• Un ángulo completo (aquél cuyo arco es una circunferencia) mide 3600.
• Un ángulo llano mide 1800.
• Un ángulo recto mide 900.
Cada uno de los 60 ángulos iguales en los que podemos dividir el ángulo de 10 mide 1 minuto
(1´), y cada uno de los 60 ángulos iguales en los que podemos dividir el ángulo de 1´ mide 1
segundo (1´´).
1 1
1´ = de 10 ⇒ 10 =60´; 1´´ = de 1´ ⇒ 1´=60´´
60 60
2.− Sistema natural
La unidad de medida en este sistema es el radián (1 rad.).
Un ángulo mide 1 radián si al trazar uno cualquiera de sus arcos, la
longitud de dicho arco coincide con la del radio con que se ha trazado.
La definición de radián no depende del radio elegido para trazar el
arco.
Un ángulo completo (3600) contiene 2·π radianes, ya que como la longitud de una circunferencia
2 ⋅π ⋅ r
es 2·π·r, contiene a su radio = 2 ⋅ π veces.
r
Luego: Un ángulo llano (1800) contendrá la mitad, es decir π radianes.
π
Un ángulo recto (900) contendrá radianes.
2
1

2. EQUIVALENCIA ENTRE LOS SISTEMAS DE MEDIDA DE ÁNGULOS
Acabamos de ver que:
π
3600 = 2·π rad. 1800 = π rad. 900 = rad.
2
Si queremos saber cuantos radianes (β rad.) mide un ángulo que mide α0, o viceversa, tendremos en
α0 180 0
cuenta la siguiente proporción: =
β rad. π rad.
EJERCICIOS:
1. −Expresa en radianes los siguientes ángulos:
450, 300, 600, 3000, 3300, 2100.
2. −Expresa en grados sexagesimales los ángulos.
3π 7π 3π 7π
rad , rad , rad , rad .
4 6 2 3
2. −¿Cuántos grados sexagesimales mide un ángulo de 1 rad.?
3. −Haz los ejercicios n0 32 y 36 de la página 136 de tu libro.
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO
Dado un ángulo α agudo (0< α <900), se definen para él los siguientes números constantes, llamados
razones trigonométricas de α.
Tomamos un punto A cualquiera, sobre cualquiera de sus lados y
trazamos la perpendicular a dicho lado por A, formándose un triángulo
rectángulo BAC.
Se definen los números siguientes:
cateto opuesto a α b
Seno de α = , sen α =
hipotenusa a
cateto contiguo a α c
Coseno de α = , cos α =
hipotenusa a
2

3. cateto opuesto a α b
Tangente de α = , tg α =
cateto contiguo a α c
Llamadas razones trigonométricas directas de α.
hipotenusa a
Cosecante de α = , cosec α =
cateto opuesto a α b
hipotenusa a
Secante de α = , sec α =
cateto contiguo a α c
cateto contiguo a α c
Cotangente de α = , cotg α =
cateto opuesto a α b
Llamadas razones trigonométricas inversas de α (por ser inversas de las anteriores).
• Veamos que las seis razones trigonométricas definidas para un ángulo α son números constantes,
es decir que, no dependen del triángulo rectángulo que hallamos formado:
Si formásemos otro triángulo rectángulo distinto BA´C´, sería
semejante al BAC (tienen los tres ángulos iguales), luego sus
lados serían proporcionales.
b a c
= =
b´ a´ c´
b b´
Por lo tanto: sen α = = ; nos daría el mismo número eligiendo un triángulo u otro.
a a´
Igual ocurre con las demás razones trigonométricas.
• Si nos fijamos en las definiciones, como la hipotenusa es mayor que cualquier cateto:
0< sen α < 1; 0<cos α <1; cosec α >1; sec α >1 (cuando α es agudo).
• Las razones trigonométricas no se expresan en ninguna unidad.
Ejemplo:
Calcula las razones trigonométricas de los ángulos agudos del siguiente triángulo rectángulo:
3 5 )
sen α = = 0,6 cosec α = = 1,6
5 3
4 5
cos α = = 0,8 sec α = = 1,25
5 4
3 4 )
tg α = = 0,75 cotg α = = 1,3
4 3
3

4. ¿Y para β? Sigue tú.
EJERCICIOS:
De la página 126 de tu libro (Santillana), haz el nº 1 y el nº 2.
De la página 136 los nº 26, 27, y 28.
RAZONES TRIGONOMÉTRICAS DE LOS ANGULOS: 30º, 45º, 60º
Estúdialo en tu libro (Ed. Santillana) (pregunta nº 3 de este tema).
EJERCICIOS:
De la página 128 los nº 7, 8 y 9.
De la página 137 los nº 45, 46, y 48.
RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS
Dado un ángulo agudo α, formamos un triángulo rectángulo cualquiera que lo tenga como uno de sus
ángulos agudos.
Se verifican las siguientes relaciones:
I) Relación fundamental de la trigonometría
Se cumple que (sen α ) 2 + (cos α ) 2 = 1 , o escrito de otra forma sen 2 α + cos 2 α = 1
Demostración:
b c
Si nos fijamos en el triángulo anterior, tenemos que sen α = , y cos α = ; por tanto
a a
b2 + c2 a 2
2 2
b c
2 2
sen α + cos α =   +   = = 2 = 1 c.q.d.
a a a2 a
T. de Pitágoras: b2 + c2 = a2
senα cos α
II) a) tg α = b) cotg α =
cosα senα
4

5. Demostración:
 b
 sen α a b·a b
= = = = tag α
b   cos α
a) c.q.d.
c c·a c
senα =  
a  a
⇒
c c
cos α =  
a  b) cosα = a = c·a = c = cotg α
 c.q.d.
 senα b b·a b

 a
1 1 1
III) a) cosec α = b) sec α = c) cotg α =
senα cos α tagα
Demostración:
b 1 1 a
a) Como sen α = , tendremos que = = = cosecα c.q.d.
a senα b b
a
Igual se demuestran las demás.
IV) Relaciones secundarias:
a) 1 + tg2 α = sec2 α b) 1 + cotg2 α = cosec2 α
Demostración:
 senα  sen 2α cos 2 α + sen 2α
2
1
2
a) 1 + tg α = 1 +   = 1+ = = = sec 2 α c.q.d.
 cosα  cos α
2
cos α
2
cos α
2
 cos α  cos 2α sen 2α + cos 2α
2
1
2
b) 1 + cotg α = 1 +   = 1+ = = = cosec 2α c.q.d.
 sen α  sen α
2
sen α
2
sen 2α
EJERCICIOS:
De la página 127 de tu libro, haz el nº 4 y el nº 5.
De la página 136 los nº 34, 35, 36, 40, 41, 42, 43, 44.
Uso de la calculadora.
RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
Resolver un triángulo es calcular todos sus elementos, es decir, calcular todos sus lados y ángulos
desconocidos.
Para ello es necesario conocer como mínimo tres de sus elementos, siendo por lo menos uno de ellos
un lado.
5

6. Si el triángulo que queremos resolver es rectángulo, tendremos en cuenta:
• El Teorema de Pitágoras a2 = b2 + c2
• B + C = 90º
ˆ ˆ
• ˆ ˆ
La definición de las razones trigonométricas de B y C , y las
relaciones entre ellas.
• El Teorema del cateto y el Teorema de la altura.
EJERCICIO:
En un triángulo rectángulo se conocen la hipotenusa a = 5 cm. y un cateto b = 4 cm. Calcula los
demás elementos.
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO CUALQUIERA
AMPLIACIÓN DEL CONCEPTO DE ÁNGULO
La interpretación del ángulo como la porción de plano limitado por dos semirrectas con un origen
común, limita los valores de los ángulos entre 0º y 360º. Sin embargo es posible y deseable para
muchas situaciones, disponer de una definición que permita la existencia de ángulos con amplitudes
superiores a 360º o, incluso, amplitudes negativas.
Ejemplo: Para echar del todo una cerradura hay que girar la llave dos vueltas y media.
a) ¿Qué ángulo, en grados, habrá que girar la llave para abrir la cerradura?
b) Si solo está echada una vuelta y quiere cerrar del todo, ¿qué ángulo habrá que girar la llave?
Solución:
a) Hay que girar la llave 2,5 vueltas a la izquierda. Como una vuelta completa son 360º, habrá
que girar la llave 2,5·360º = 900º a la izquierda.
b) Ahora debemos girar la llave 1,5 vueltas a la derecha, es decir 1,5·360º = 540º a la derecha.
Una forma alternativa de dar los resultados sin necesidad de escribir “a la izquierda” o “a la
derecha” es escribir +900º en el apartado a y −540º en el apartado b.
El signo − indica que el giro lo hemos dado hacia la derecha (sentido en el que se mueven las agujas
de un reloj) y el signo + indica que hemos girado hacia la izquierda (sentido contrario en el que se
mueven las agujas de un reloj).
6

7. REPRESENTACIÓN DE ÁNGULOS
Para representar ángulos comprendidos entre 0º y 360º, e incluso mayores de 360º o negativos, se
utiliza la circunferencia goniométrica. Se le llama así a la circunferencia que tiene de radio la
unidad. Normalmente se toma centrada en el origen de coordenadas.
Los ángulos se representan siempre haciendo coincidir su vértice con el origen de coordenadas y su
primer lado con el semieje positivo de abscisas.
Se consideran “positivos” si el giro se hace en sentido contrario en que se mueven las agujas de
un reloj, y “negativos” si se hace en el mismo en que se mueven las agujas de un reloj.
+α
−α
Utilizando esta representación, a todo ángulo se le puede asociar un ángulo positivo comprendido
ente 0º y 360º, llamado “ángulo reducido” del primero. En la circunferencia goniométrica, el
segundo lado de un ángulo y el de su reducido coinciden.
Ejemplo:
Calcula los ángulos reducidos asociados a 1000º, −210º.
Solución: 1000º = 2·360º + 280º, ya que al dividir 1000 entre 360 se obtiene 2 de cociente y
280 de resto. Luego el ángulo reducido de 1000º es 280º.
Como −210º +360 = 150º; el, ángulo reducido de −210º es 150º.
Cuando fijamos unos ejes de coordenadas cartesianas rectangulares, el plano queda dividido en
cuatro zonas o cuadrantes.
Si un ángulo α cumple que 0º< α <90º (0 rad.< α < π/2 rad.), como el
II I segundo lado del ángulo estaría en el primer cuadrante, diremos que α es
un ángulo del primer cuadrante.
Si 90º< α < 180º (π/2 rad. < α <π rad.) sería del segundo cuadrante,
III IV
etc…
Lo resumimos en la tabla siguiente:
7

8. 1er Cuadrante 2º Cuadrante 3er Cuadrante 4º Cuadrante
0º < α <90º 90º < α < 180º 180º < α < 270º 270º < α < 360º
π π 3π 3π
0 rad.< α < rad. rad. < α < π rad. π rad. < α < rad. rad. < α < 2π rad.
2 2 2 2
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO DEL 1er CUADRANTE
En la figura siguiente se ha representado un ángulo
A”
del primer cuadrante α.
Sea A el punto de corte del segundo lado del ángulo
con la circunferencia goniométrica y A´ su
proyección sobre el primer lado (eje OX).
α Sea B el punto de corte de la circunferencia
goniométrica con el eje OX y A´´ el punto de corte
del segundo lado del ángulo con la perpendicular al
eje OX en el punto B.
Recordando las definiciones de las razones
trigonométricas para ángulos agudos y teniendo en
cuenta que la hipotenusa del triángulo rectángulo OA´A mide 1, tendremos que:
____ ____
AA´ AA´ ____
sen α = = = AA´ , que es la ordenada del punto A.
OA 1
OA´ OA´ ____
cos α = = = OA´ , que es la abscisa del punto A.
OA 1
____
ordenada del punto A AA´ A" B A" B
tg α = = = = A" B , que es la ordenada del punto A”.
abscisa del punto A OA´ (∗) OB 1
(∗) Tma de Thales, pues OA´A ∼ OBA”
Esta nueva definición de las razones trigonométricas en función de las coordenadas de puntos se
puede extender y aplicar fácilmente a cualquier ángulo no agudo.
8

9. RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO DEL RESTO DE LOS CUADRANTES
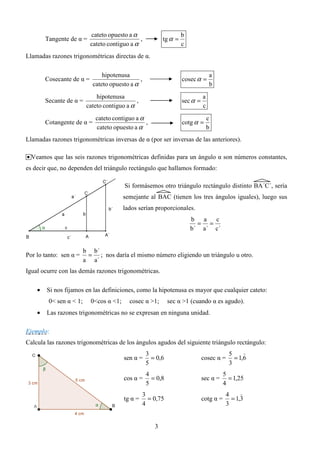
Si α es un ángulo del 2º, 3º, o 4º cuadrante, en todos los casos este ángulo determina los puntos A y
A”, cuyas coordenadas nos van a dar las razones trigonométricas de acuerdo con la definición
utilizada en el caso del primer cuadrante.
Así, si A(x, y) y A”(1, y”), se definen: sen α = y cos α = x tg α = y”
2º CUADRANTE: 3er CUADRANTE 4º CUADRANTE
α tg α
α α
α
tg α tg α
Teniendo en cuenta el signo de las coordenadas de un punto en los distintos cuadrantes, se determina
de forma inmediata el signo de las razones trigonométricas de un ángulo si se sabe en qué cuadrante
se encuentra su ángulo reducido correspondiente. α
Cuadrante de α sen α cos α tg α
I (+, +) + + +
II (−, +) + − −
III (−, −) − − +
IV (+, −) − + −
VALOR DE LAS RAZONES TRIGONOMÉTRICAS
A partir de la definición, es fácil ver que:
−1 ≤ sen α ≤ 1 −1 ≤ cos α ≤ 1 − ∞ < tg α < + ∞
Al ser la cosecante y la secante las razones inversas del seno y del coseno respectivamente, sus
signos coinciden con los de éstos y se cumple que:
cosec α ∈ (− ∞, −1] ∪ [1, + ∞] sec α ∈ (− ∞, −1] ∪ [1, + ∞)
En el caso de la cotangente, como inversa de la tangente, coincide con su signo en cada cuadrante y
puede tomar cualquier valor real. − ∞ < cotg α < + ∞
9

10. También aplicando la definición, tendremos que:
α sen α cos α tg α cosec α sec α cotg α
0º = 0 rad. 0 1 0 No definida 1 No definida
90º = π/2 rad. 1 0 No definida 1 No definida 0
180º = π rad. 0 −1 0 No definida −1 No definida
270º = 3π/2 rad −1 0 No definida −1 No definida −1
OBSERVACIÓN:
A”
Aunque se ha utilizado una circunferencia de radio la unidad
para extender la definición de las razones trigonométricas, el
r y´ procedimiento habría sido igual para un radio diferente.
y En este caso, las razones trigonométricas no serían
α
directamente las coordenadas de A y A”, sino divididas por el
x
radio de la circunferencia utilizada:
y x y´
sen α = cos α = tg α =
r r r
EJERCICIO: Indica el signo de las razones trigonométricas directas de los ángulos siguientes:
a) 120º b) −70º c) 256º d) 800º e) 315º f) 1200º
11π 4π 7π 9π
g) 55º h) −460º i) rad. j) rad. k) − rad. l) − rad.
3 3 6 4
REDUCCIÓN AL PRIMER CUADRANTE
Consiste en relacionar las razones trigonométricas de un ángulo cualquiera con las razones
trigonométricas de un ángulo agudo (ángulo que pertenece al primer cuadrante).
10

11. ÁNGULOS DEL SEGUNDO CUADRANTE: ÁNGULOS SUPLEMENTARIOS
Si β es un ángulo del segundo cuadrante, existe un
ángulo α del primer cuadrante (su suplementario) tal
r =1 que β = 180º − α (α + β = 180º y α=180º− β).
Los triángulos OA´A y OC´C son iguales, luego:
sen β = CC´ = AA´ = sen α
cos β = − OC´ = −OA´ = −cos α
tg β = − BD = −A" B = −tg α
Resumiendo:
Si la unidad angular que manejamos fuese el grado sexagesimal,
sen β = sen (180º −β) cos β = − cos (180º −β) tg β = −tg (180º −β)
Si la unidad fuese el radián,
sen β = sen (π −β) cos β = − cos (π − β) tg β = −tg (π −β)
EJERCICIO: Calcula las razones trigonométricas del ángulo de 150º, mediante la reducción al
primer cuadrante..
ÁNGULOS DEL TERCER CUADRANTE: ÁNGULOS QUE DIFIEREN EN 180º
Si β pertenece al tercer cuadrante, existe un ángulo α
del primer cuadrante (que se diferencia de β en 180º) tal
r =1 que β = 180º + α (α = β −180º).
Los triángulos OA´A y OC´C son iguales, luego:
sen β = − CC´ = −AA´ = −sen α
cos β = − OC´ = −OA´ = −cos α
tg β = A" B = tg α
Resumiendo:
Si la unidad angular que manejamos fuese el grado sexagesimal,
11

12. sen β = −sen (β − 180º)
β cos β = − cos (β − 180º)
β tg β = tg (β − 180)
β
Si la unidad fuese el radián,
sen β = −sen (β − π)
β cos β = − cos (β − π)
β tg β = tg (β −π)
β
EJERCICIO: Calcula las razones trigonométricas del ángulo de 210º, mediante la reducción al
primer cuadrante.
ÁNGULOS DEL CUARTO CUADRANTE: ÁNGULOS QUE SUMAN 360º. ÁNGULOS
OPUESTOS
•
Si β es un ángulo del cuarto cuadrante, existe un ángulo
α del primer cuadrante (que es la diferencia hasta 360º
de β), que cumple que β = 360º − α (α = 360º − β).
r =1
Los triángulos OA´A y OA´C son iguales, luego:
sen β = − A´C = − AA´ = −sen α
cos β = OA´ = cos α
D tg β = − BD = −A" B = −tg α
Resumiendo:
Si la unidad angular que manejamos fuese el grado sexagesimal,
sen β = −sen (360º −β ) cos β = cos (360º −β ) tg β = −tg (360º −β)
Si la unidad fuese el radián,
sen β = −sen (2π−β) cos β = −cos (2π − β) tg β = −tg (2π −β)
EJERCICIO: Calcula las razones trigonométricas del ángulo de 330º, mediante la reducción al
primer cuadrante.
• Dado un ángulo α, si representamos los ángulos
360º−α y −α (opuesto de α) en la circunferencia r =1
goniométrica; el segundo lado de ambos ángulos es el
mismo. Por tanto también lo serán sus razones
trigonométricas, luego podemos escribir:
12

13. sen(−α) = −sen(360º −α) = −sen α
− cos(−α) = cos(360º−α) = cos α
− −
tg(−α) = −tg(360º −α) = −tg α
−
RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ÁNGULOS
COMPLEMENTARIOS
Si β es el ángulo complementario de α, se cumple que
β = 90º −α (α +β =90º y α = 90º −β)
Los triángulos OA´A y OB´B son iguales, luego:
sen β = BB´ = OA´ = cos α
O cos β = OB´ = AA´ = sen α
sen β cos α
tg β = = = cotg α
cos β senα
Resumiendo:
Si la unidad angular que manejamos fuese el grado sexagesimal,
sen β = cos (90º −β ) cos β = sen (90º −β ) tg β = cotg (90º −β)
Si la unidad fuese el radián,
π −
sen β = cos (π/2−β) cos β = sen (π/2 − β)
π tg β = cotg (π/2 −β)
π
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS β ∉ [0, 360º)
Las razones trigonométricas de un ángulo β ∉ [0, 360º) son las de su ángulo reducido, ya que al
representarlos en la circunferencia goniométrica el segundo lado de ambos coincide.
Puede ocurrir que:
1. β ≥ 360º. En este caso para calcular el ángulo reducido habrá que dividir β entre 360º. Si
llamamos n al cociente y α al resto de dicha división, tendremos que β = 360·n + α. Por tanto
α es su ángulo reducido.
Ejemplo: Si β = 940º, dividimos 940 entre 360 y obtenemos 2 de cociente y 220 de resto.
Luego 940º = 360º·2 + 220. El ángulo reducido de 940º es 220º.
13

14. 2. β < 0º
a. Si −360º < β < 0, su ángulo reducido será α = β + 360º.
Ejemplo: Si β = −60º, su ángulo reducido es α = (−60º) + 360º = 300º. Las razones
trigonométricas de −60º serán las mismas que las de 300º.
b. Si β ≤ −360º, dividimos −β (que será positivo) entre 360º. Llamando n al cociente y α
al resto de dicha división (α<360º), tendremos que −β = 360·n + α. Multiplicando por
−1 los dos miembros, β = −360·n − α. Las razones trigonométricas de β serán iguales
a las de −α; y como −360º<−α <0º, se calculan como en el apartado “a”.
Ejemplo: Calcula las razones trigonométricas de β = −780º
Dividimos −(−780) = 780 entre 360, el cociente es 2 y el resto 60, luego
780 = 2·360 + 60 ⇒ −780 = −2·360 −60. Por tanto las razones trigonométricas de
−780º serán las mismas que las de −60º, (que ya vimos como se calculan en el
apartado “a”).
14