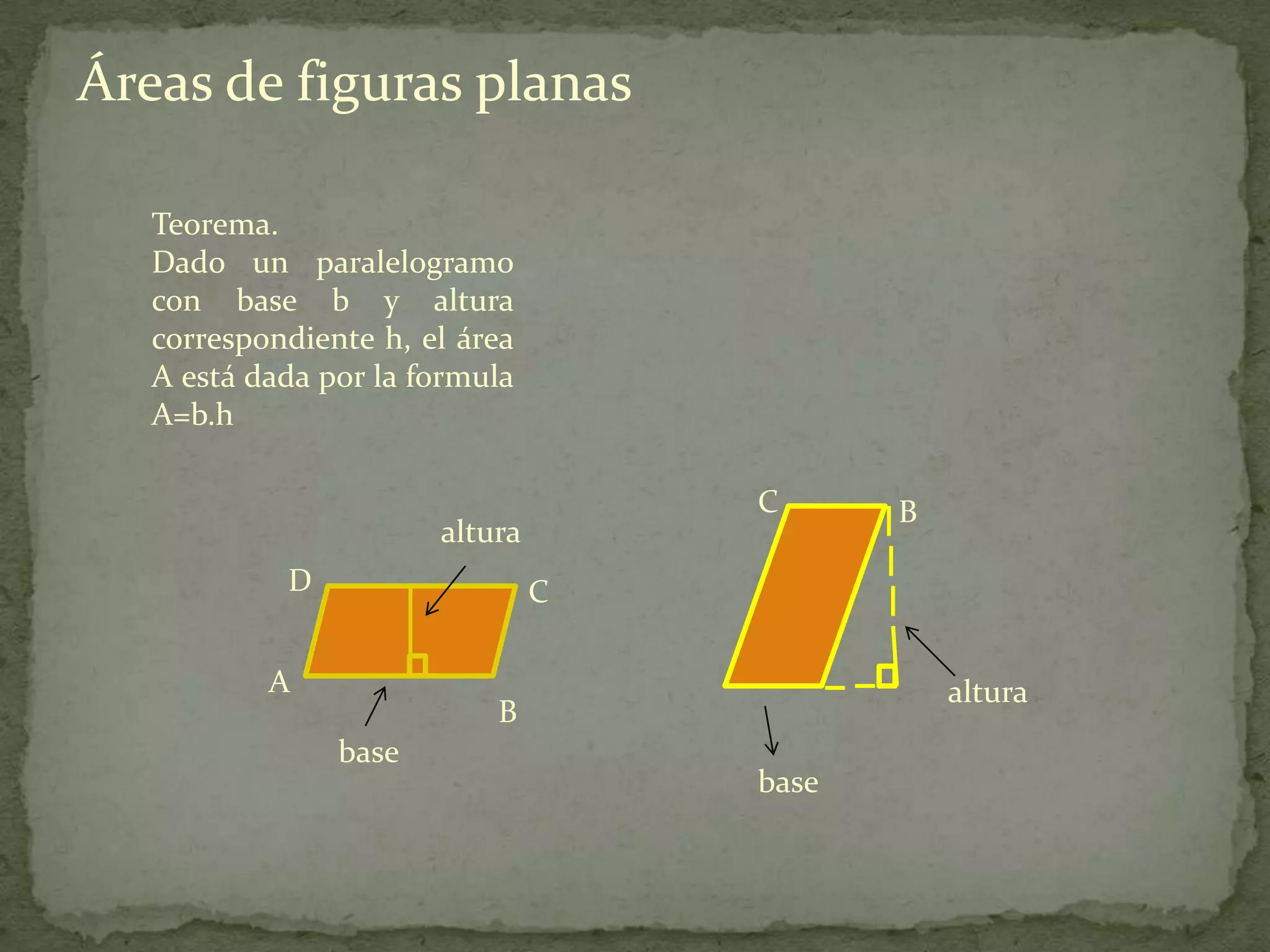
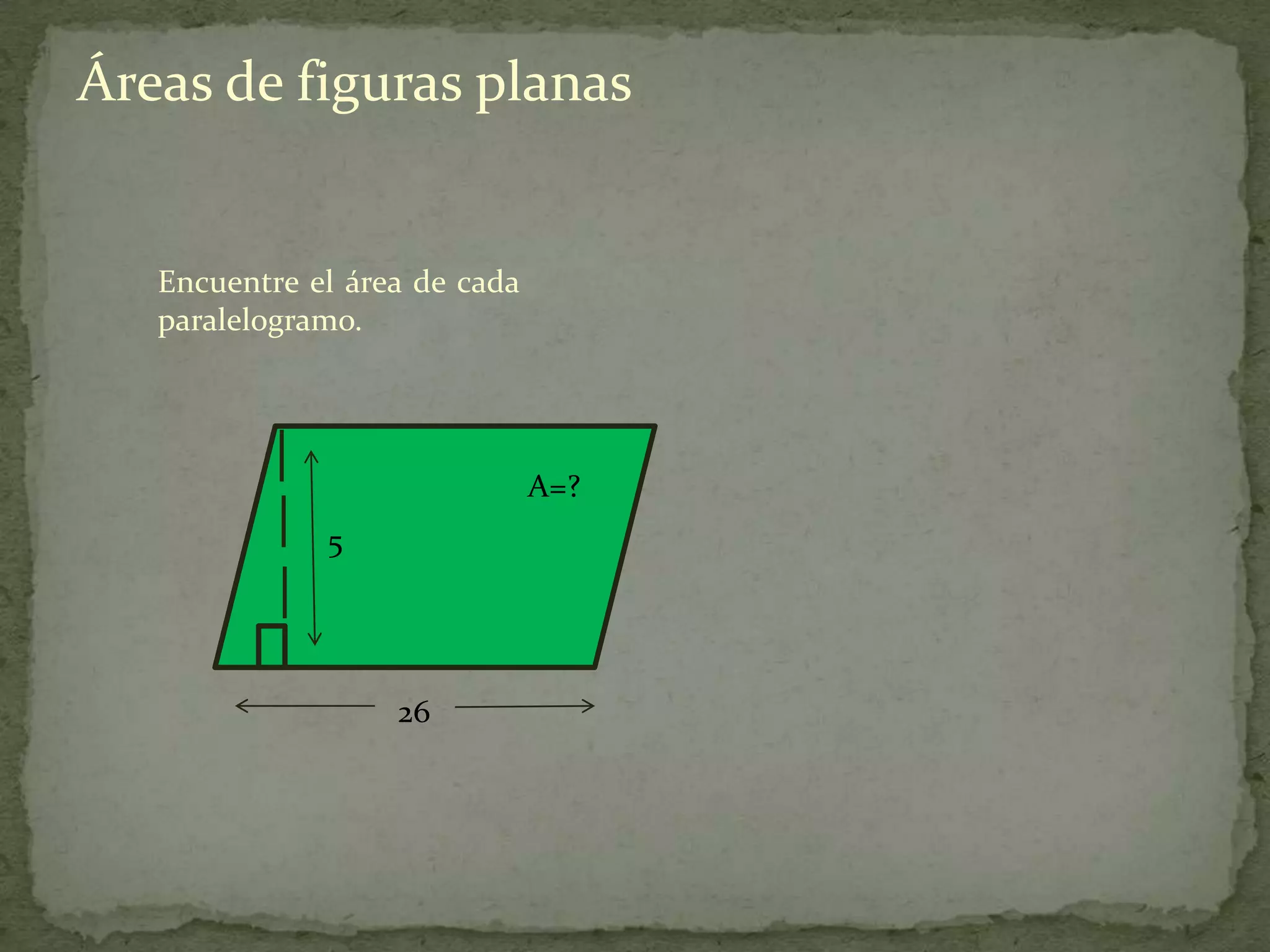
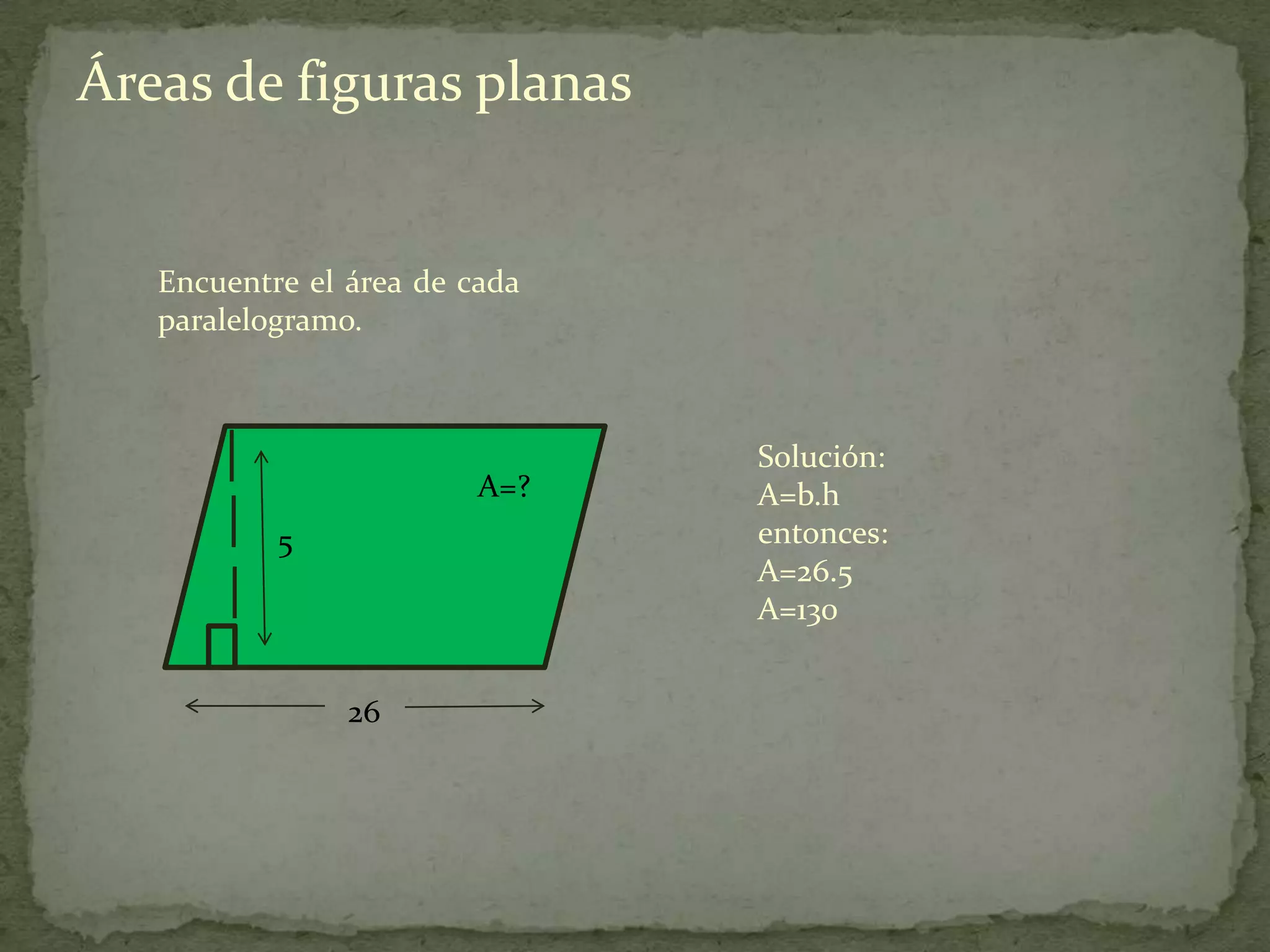
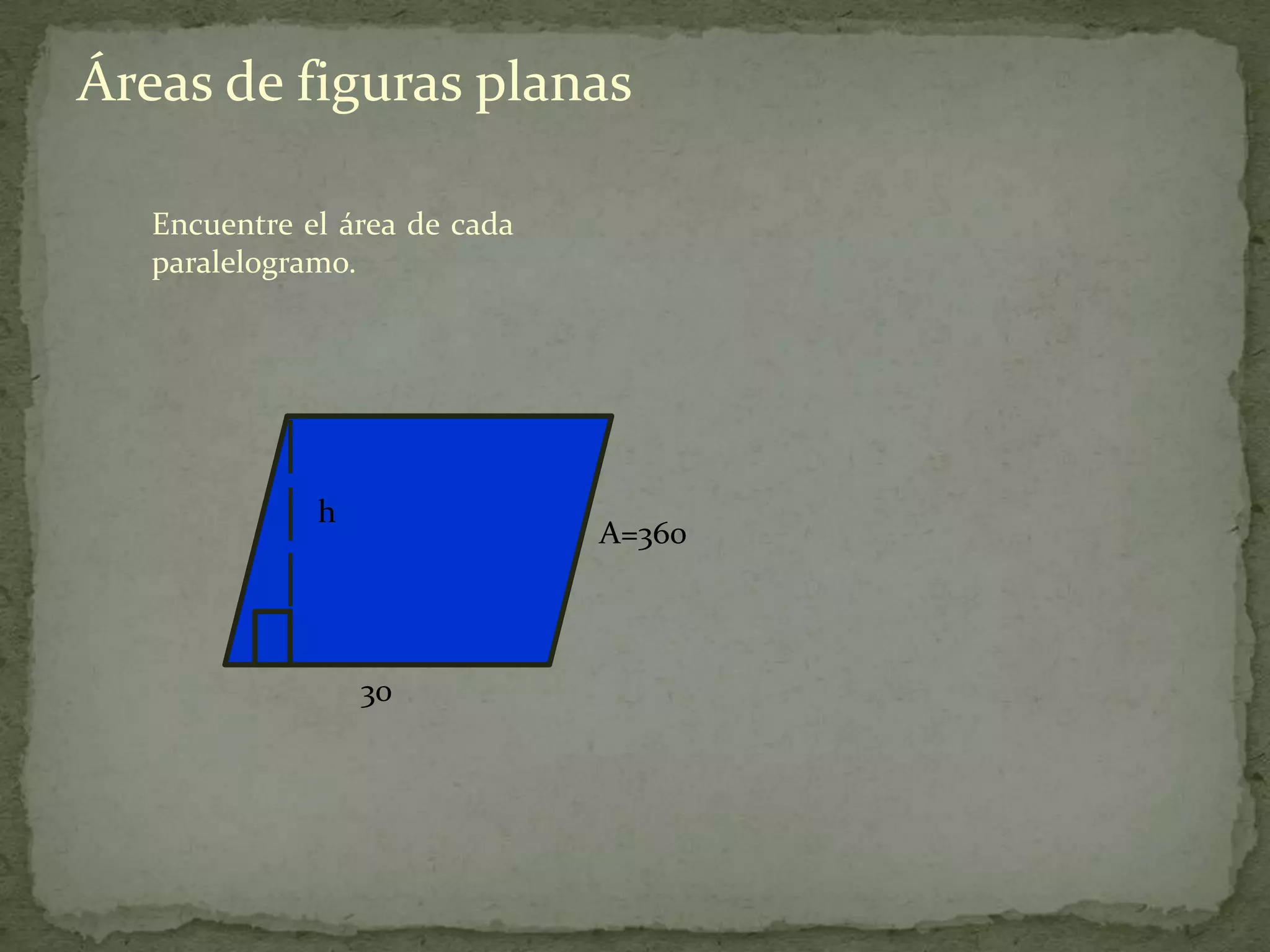
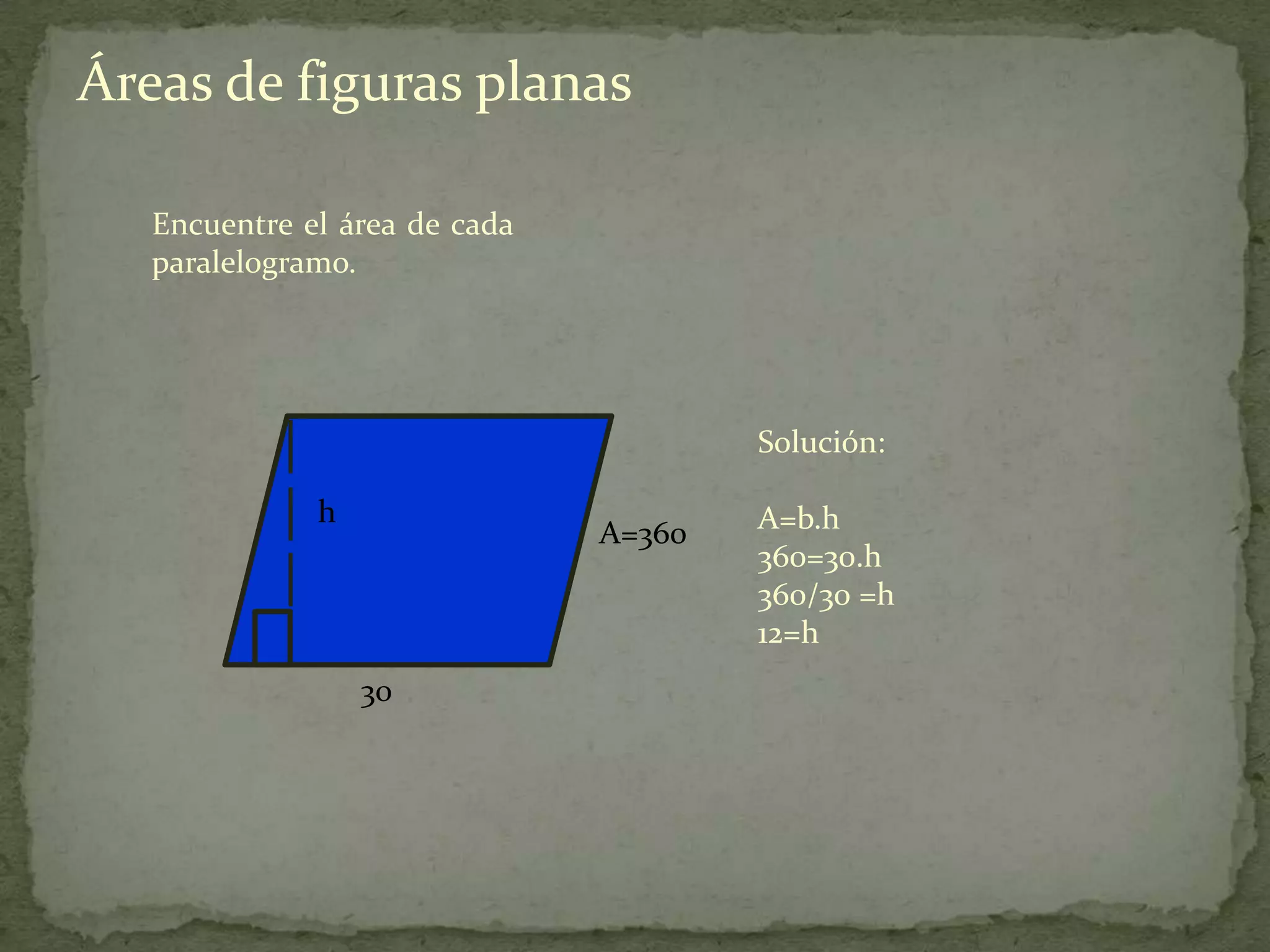
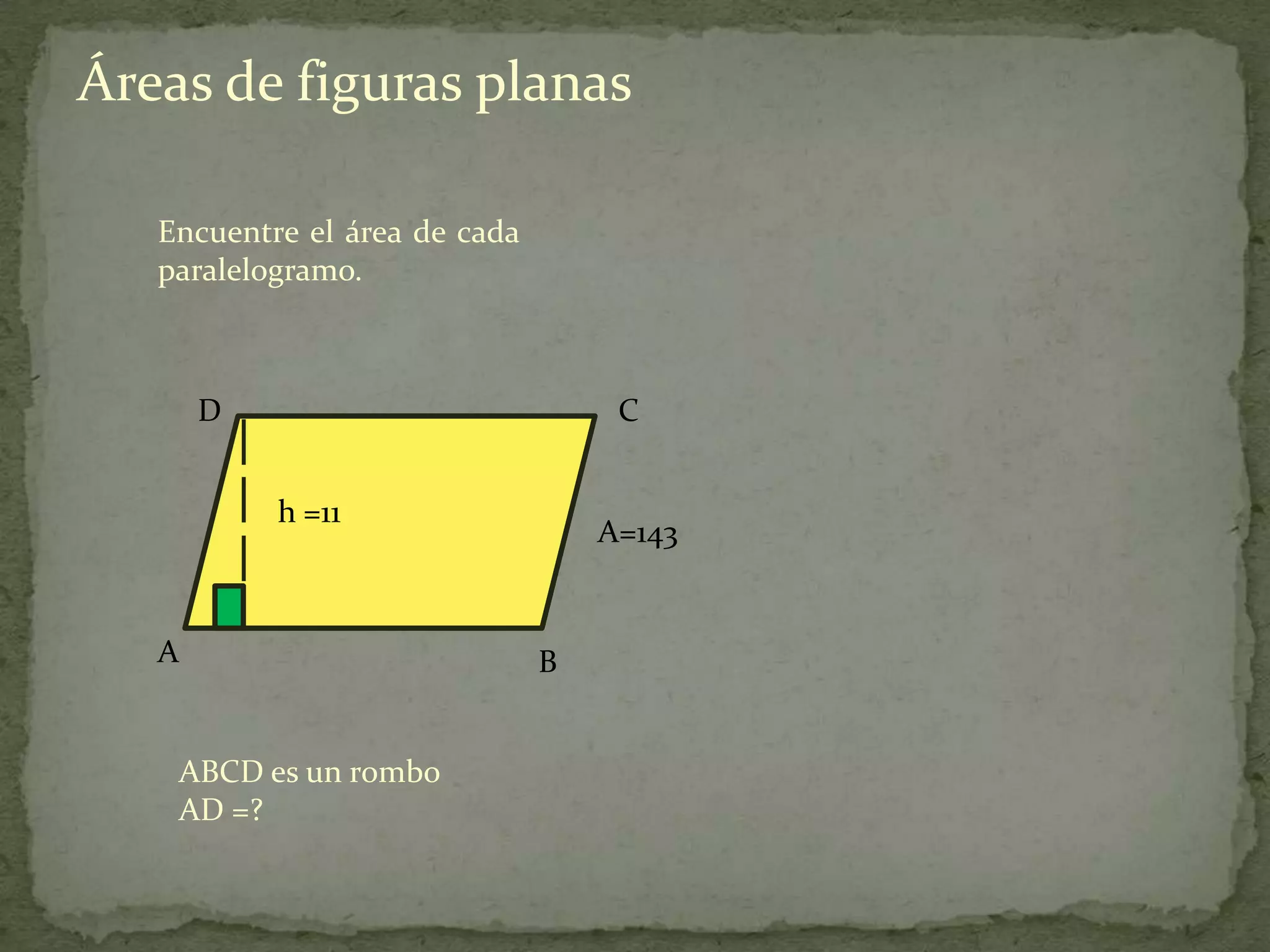
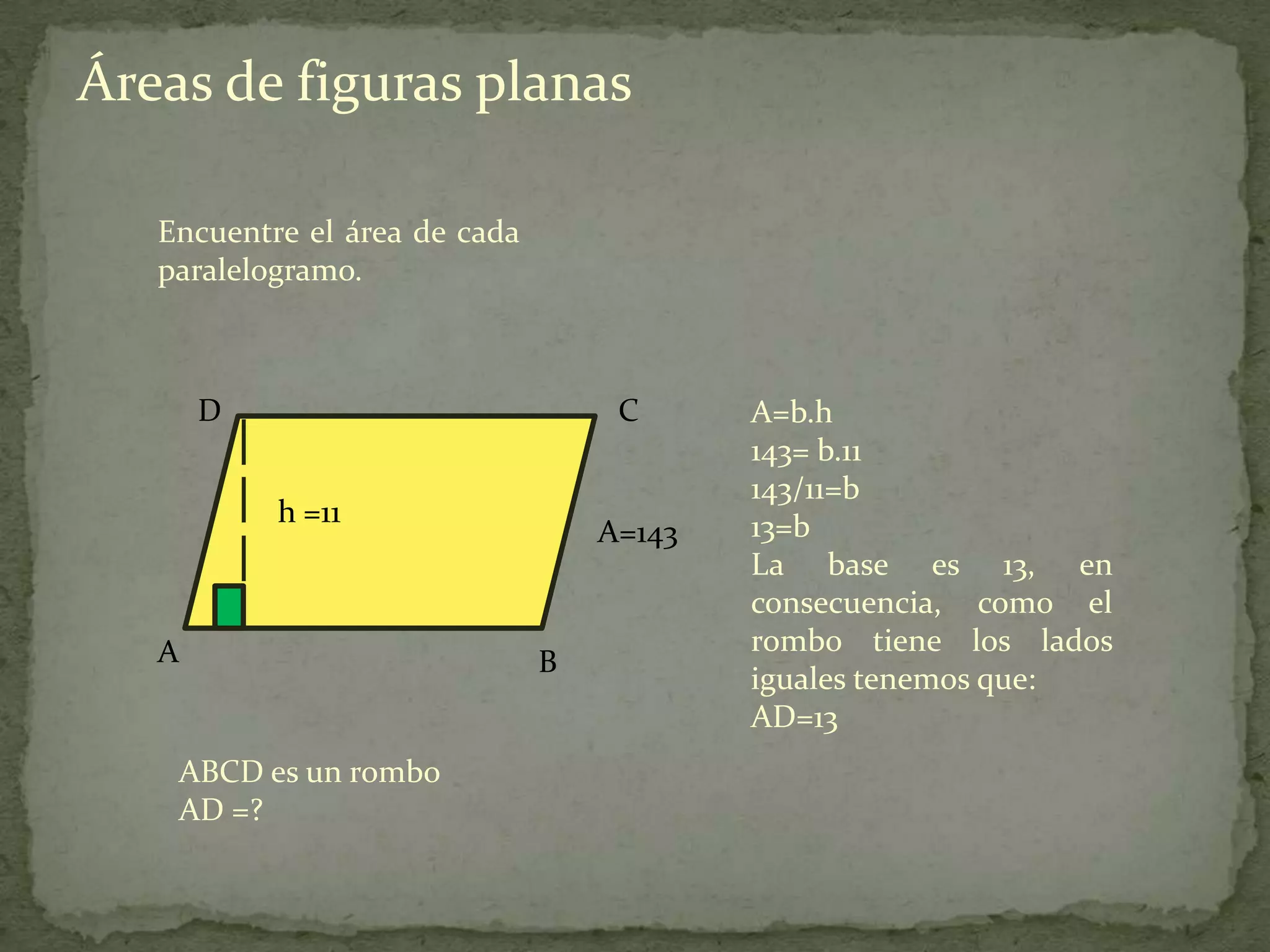
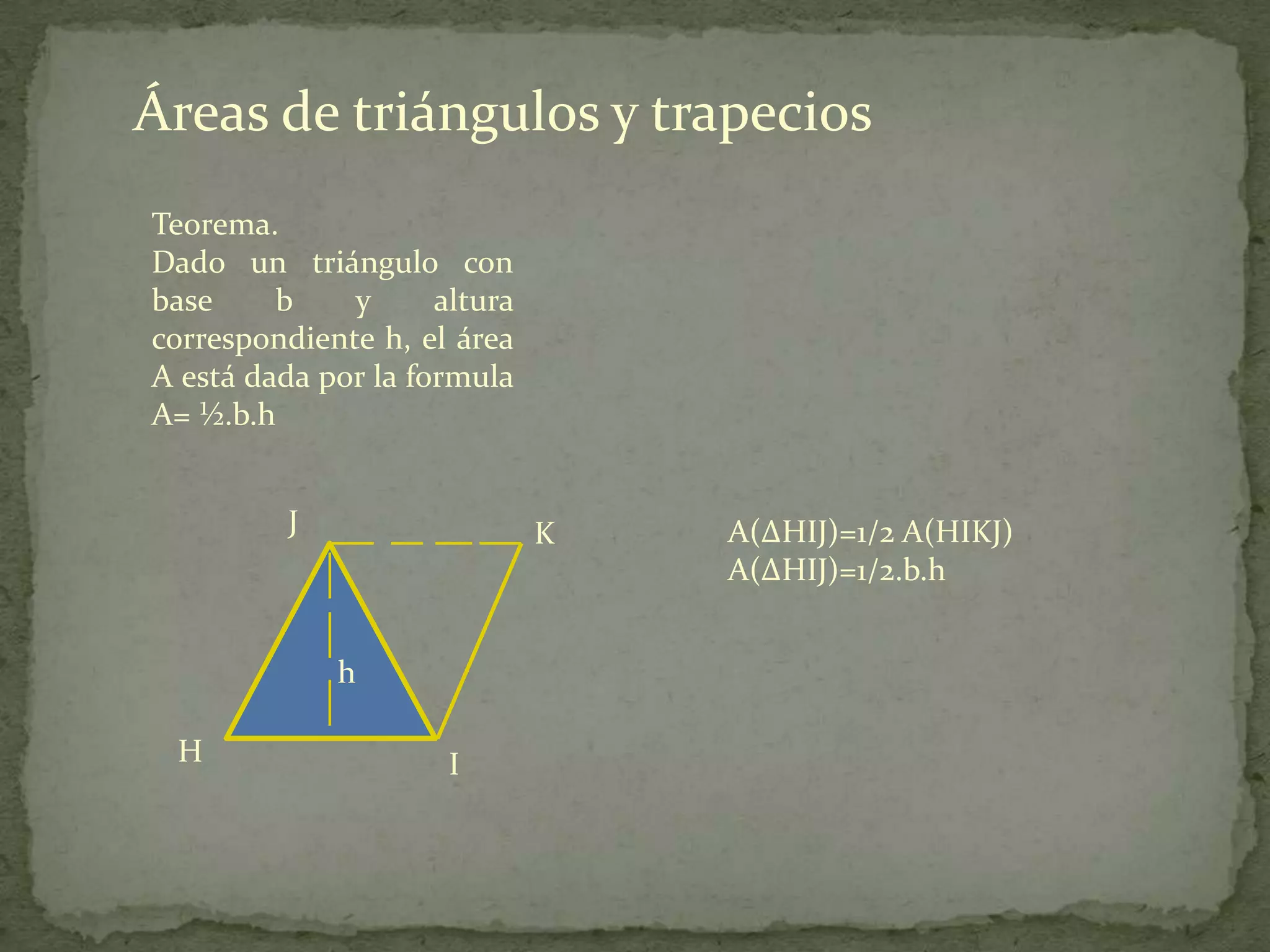
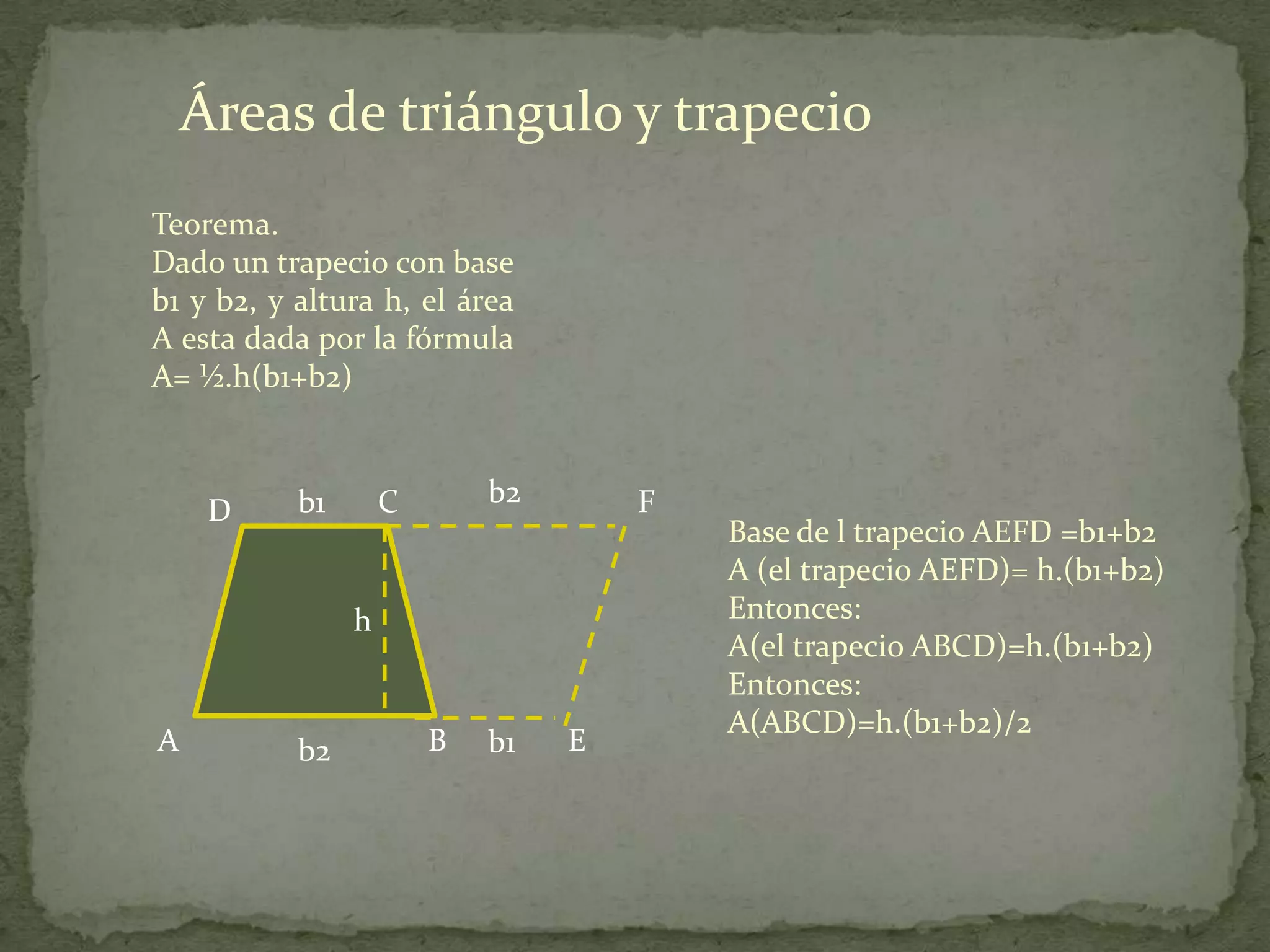
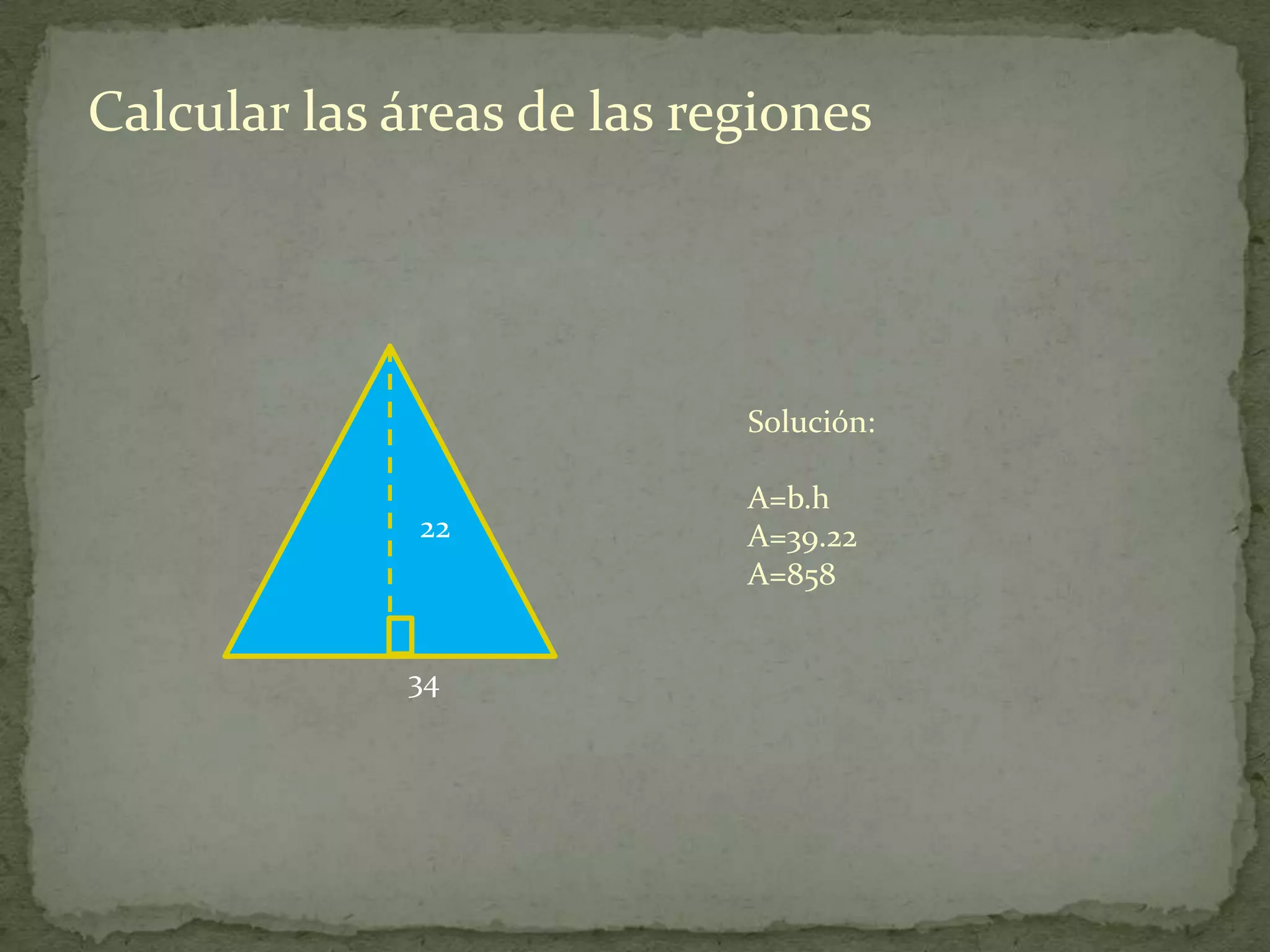
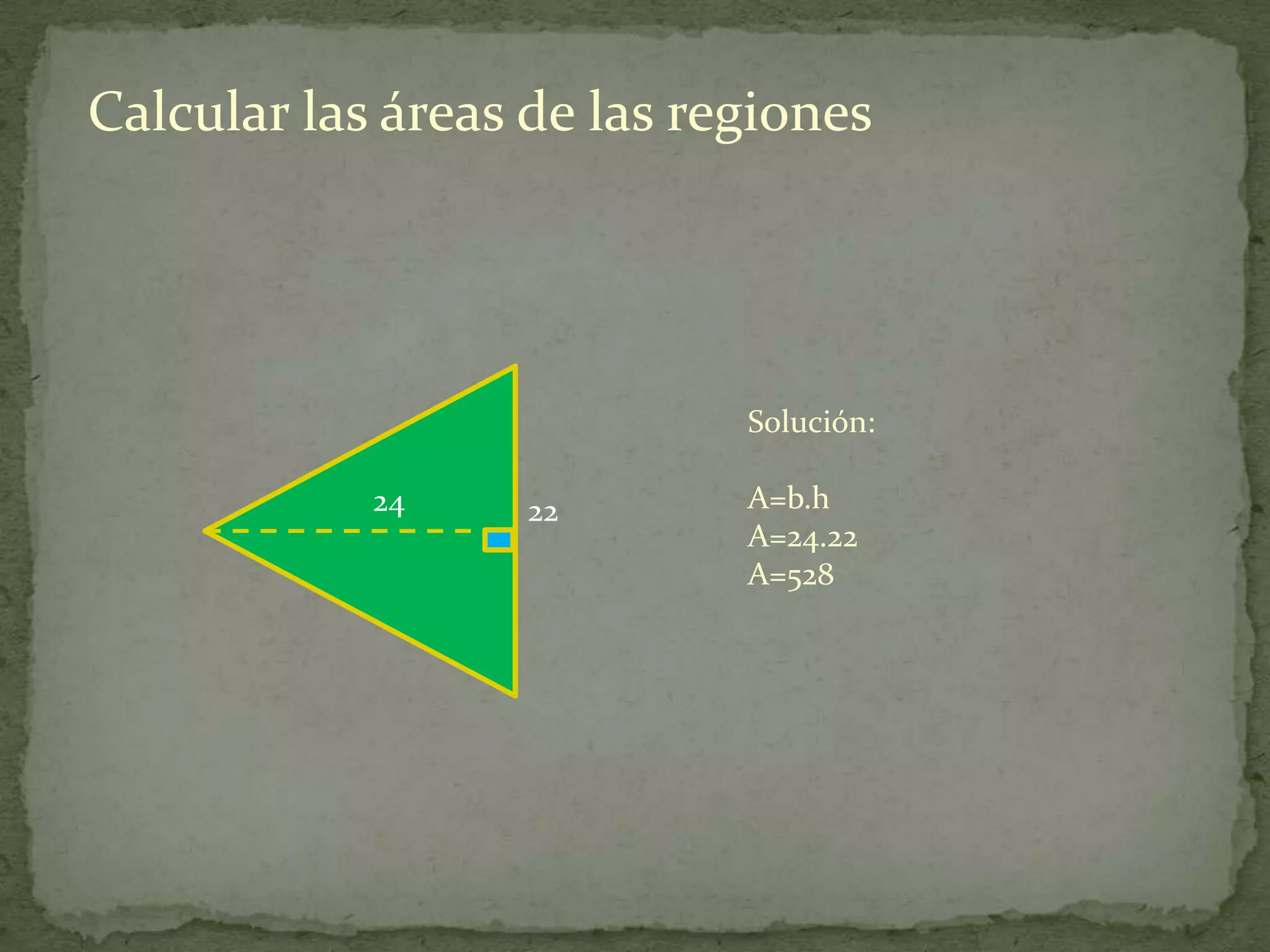
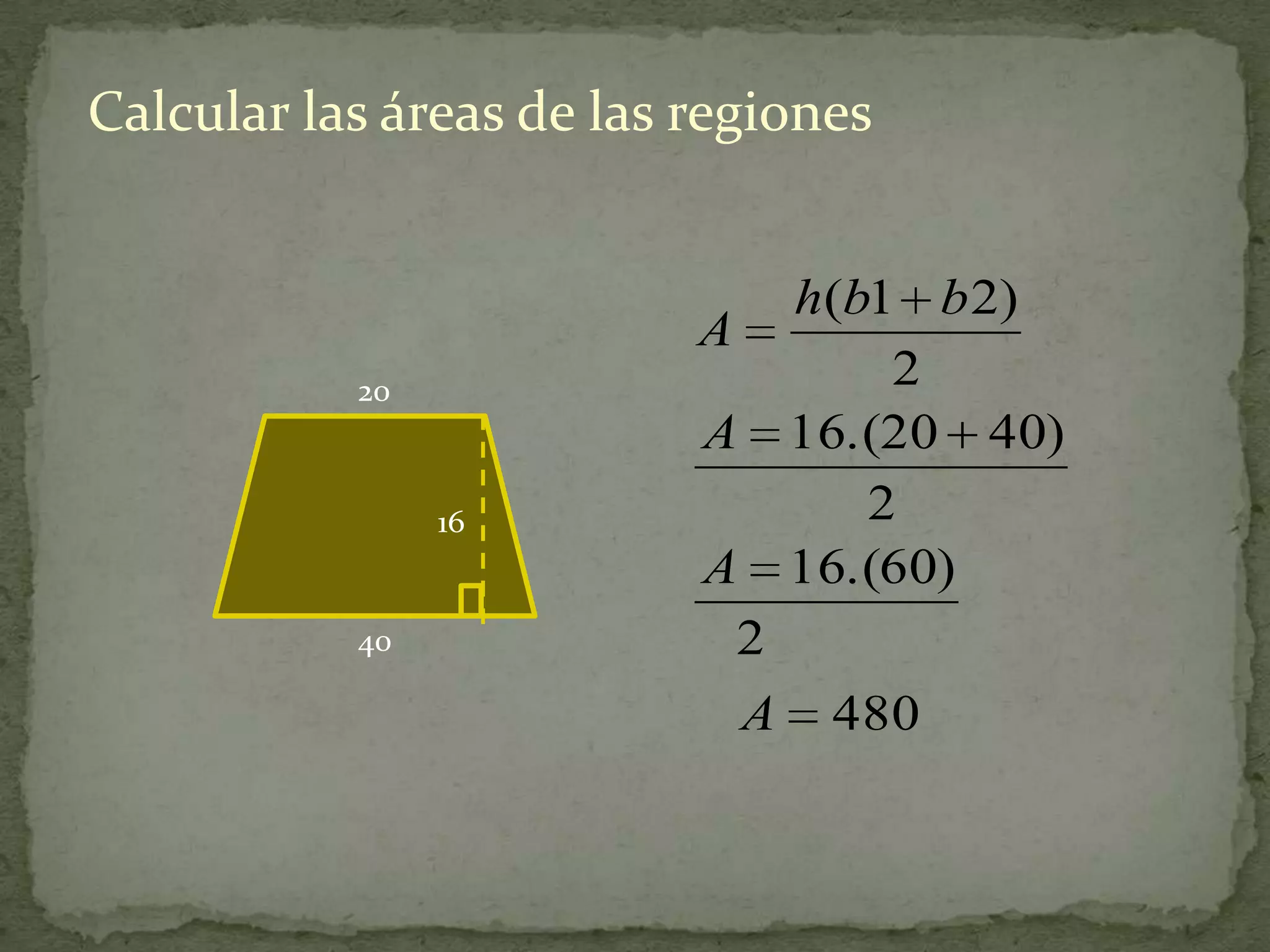
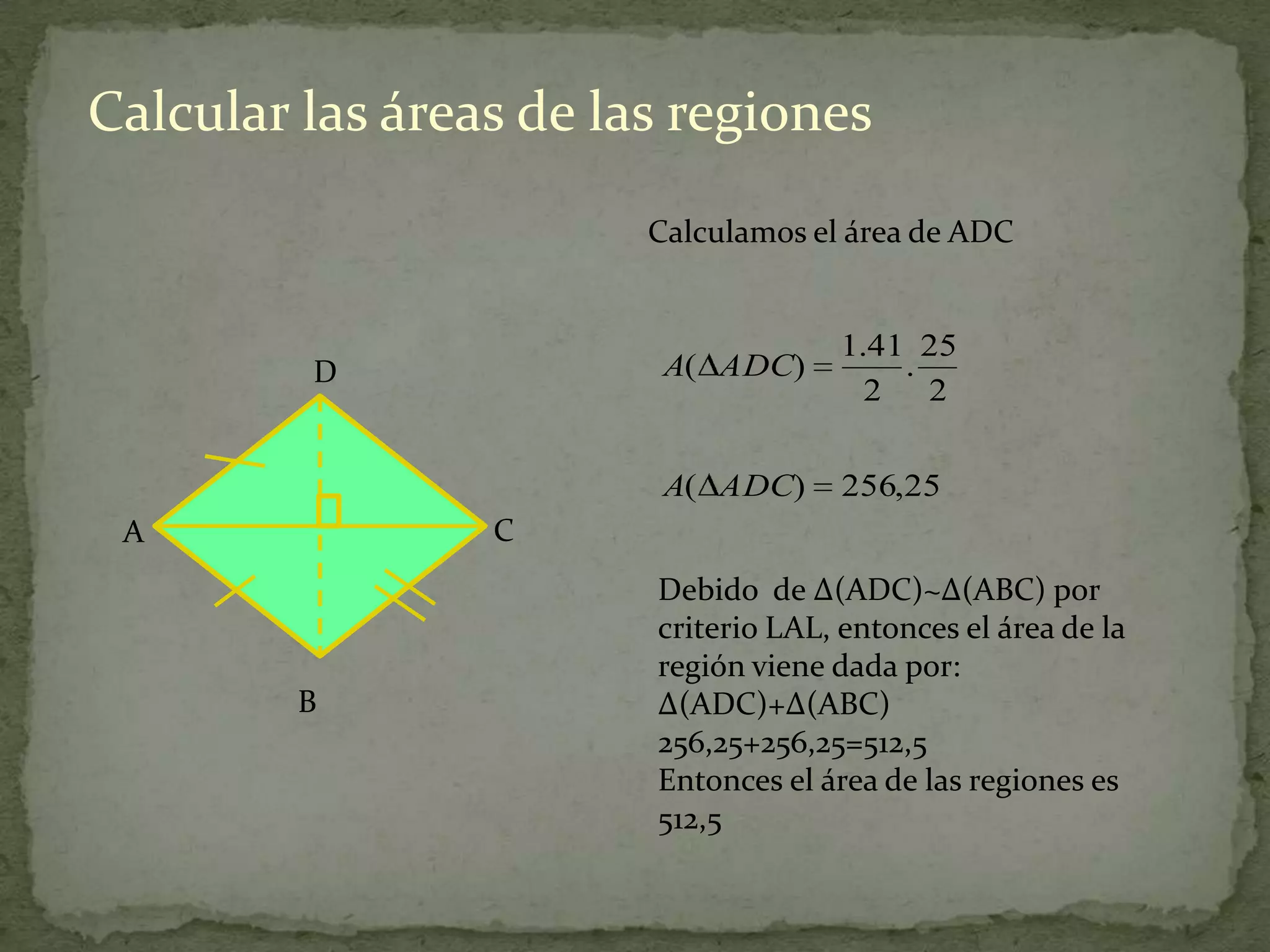
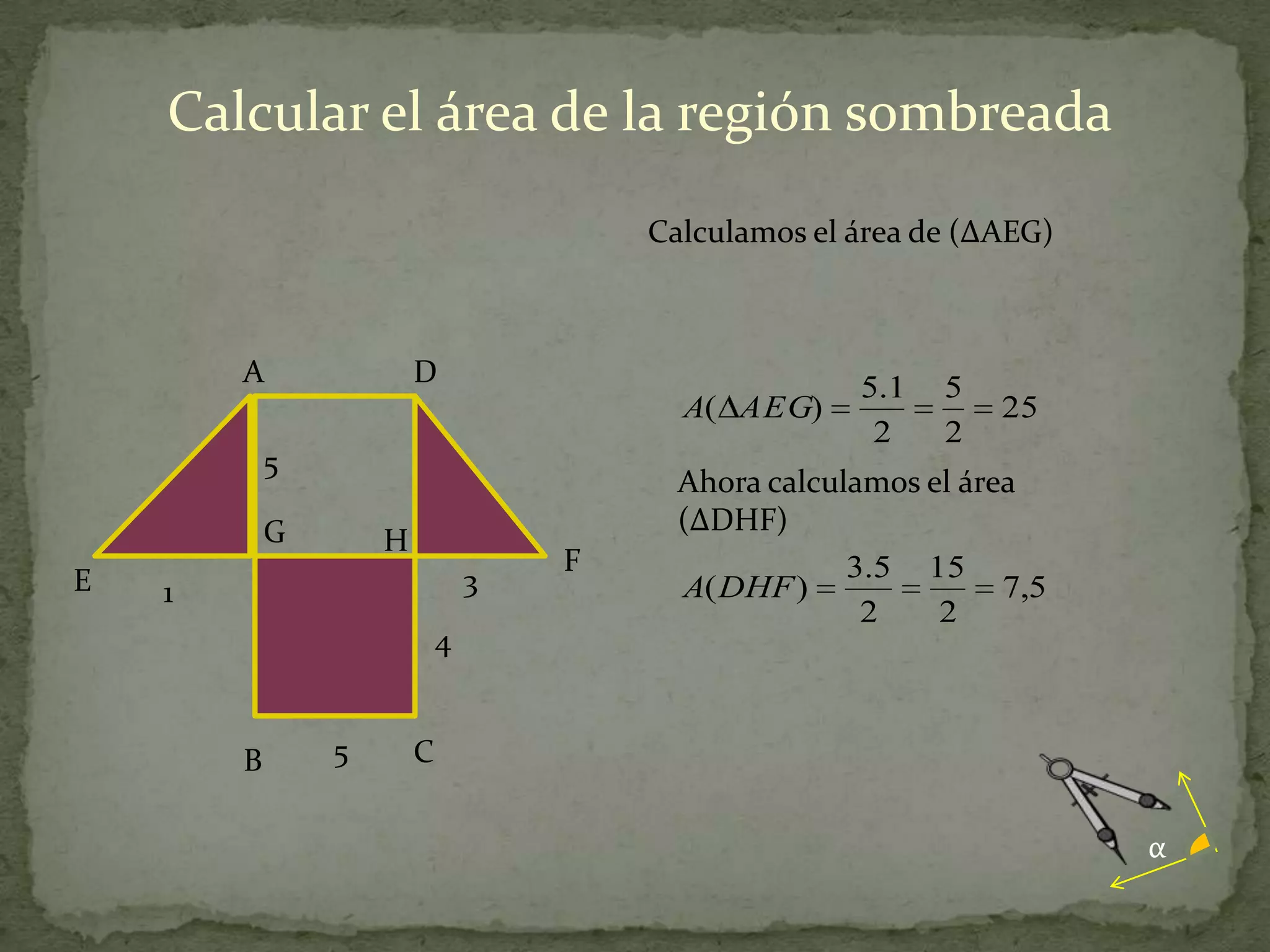
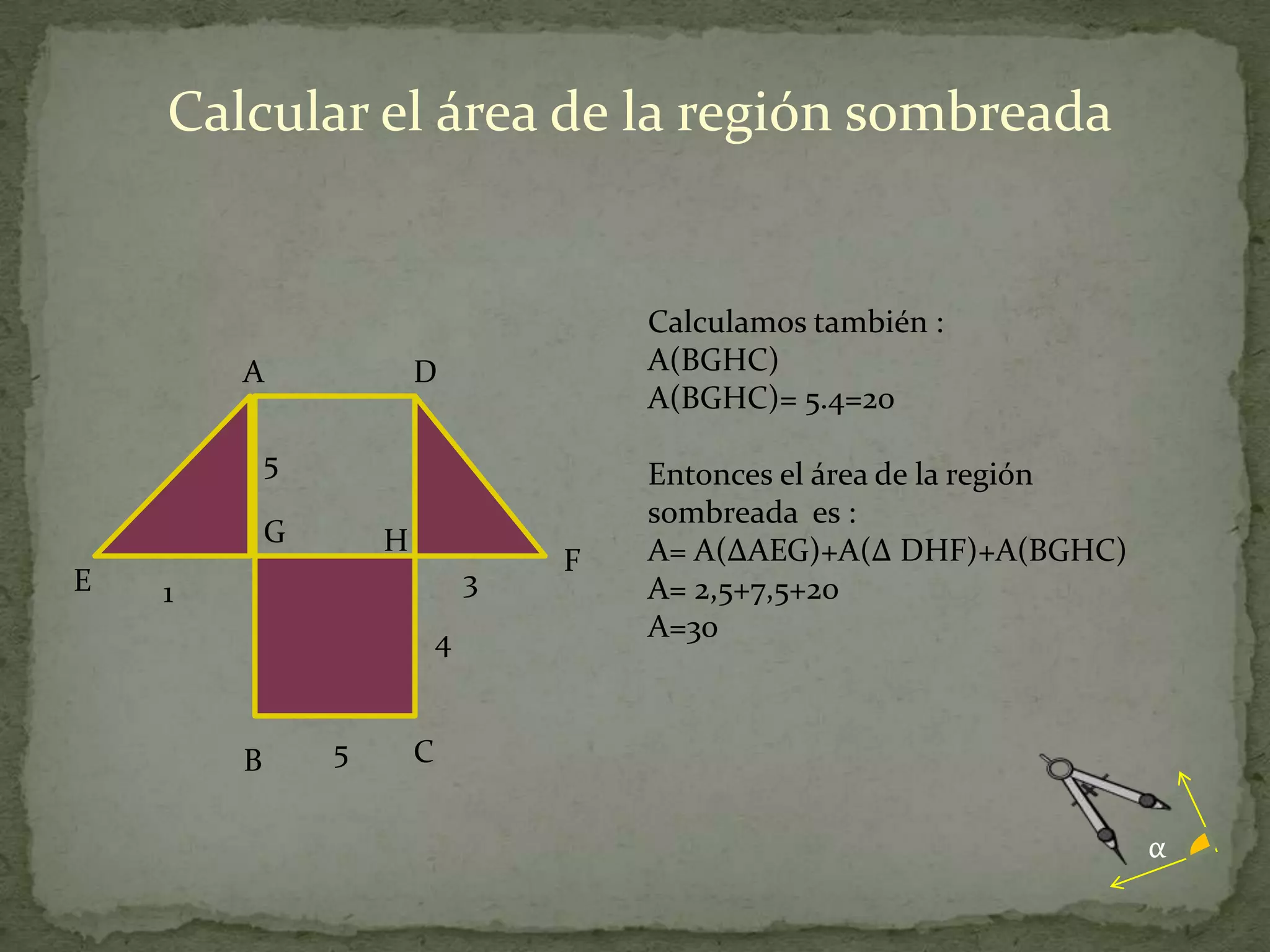
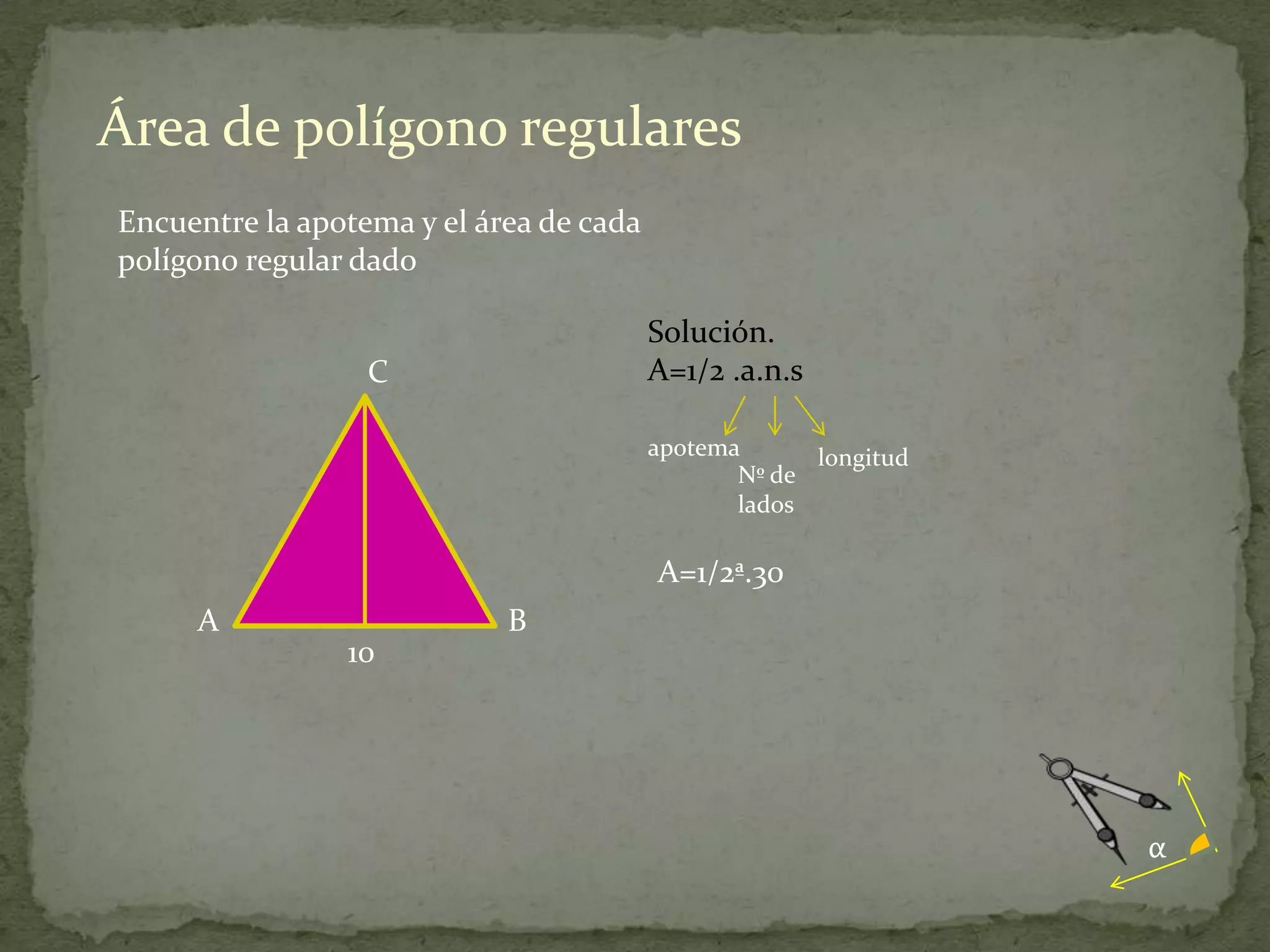
Este documento presenta información sobre cómo calcular el área de diferentes figuras planas como paralelogramos, triángulos, trapecios, polígonos regulares y regiones sombreadas. Explica las fórmulas para calcular el área de cada figura y proporciona ejemplos resueltos de cómo aplicar las fórmulas.

1. Aplicar las reglas correspondientes
para el calculo de áreas de figuras
planas.
Licdo. Víctor Monsalve

2. Áreas de figuras planas
Teorema.
Dado un paralelogramo
con base b y altura
correspondiente h, el área
A está dada por la formula
A=b.h
C B
altura
D C
A altura
B
base
base

3. Áreas de figuras planas
Encuentre el área de cada
paralelogramo.
A=?
5
26

4. Áreas de figuras planas
Encuentre el área de cada
paralelogramo.
Solución:
A=? A=b.h
5 entonces:
A=26.5
A=130
26

5. Áreas de figuras planas
Encuentre el área de cada
paralelogramo.
h
A=360
30

6. Áreas de figuras planas
Encuentre el área de cada
paralelogramo.
Solución:
h A=b.h
A=360
360=30.h
360/30 =h
12=h
30

7. Áreas de figuras planas
Encuentre el área de cada
paralelogramo.
D C
h =11
A=143
A B
ABCD es un rombo
AD =?

8. Áreas de figuras planas
Encuentre el área de cada
paralelogramo.
D C A=b.h
143= b.11
143/11=b
h =11 13=b
A=143
La base es 13, en
consecuencia, como el
A rombo tiene los lados
B
iguales tenemos que:
AD=13
ABCD es un rombo
AD =?

9. Áreas de triángulos y trapecios
Teorema.
Dado un triángulo con
base b y altura
correspondiente h, el área
A está dada por la formula
A= ½.b.h
J K A(∆HIJ)=1/2 A(HIKJ)
A(∆HIJ)=1/2.b.h
h
H I

10. Áreas de triángulo y trapecio
Teorema.
Dado un trapecio con base
b1 y b2, y altura h, el área
A esta dada por la fórmula
A= ½.h(b1+b2)
b1 C b2 F
D
Base de l trapecio AEFD =b1+b2
A (el trapecio AEFD)= h.(b1+b2)
h Entonces:
A(el trapecio ABCD)=h.(b1+b2)
Entonces:
A(ABCD)=h.(b1+b2)/2
A b2 B b1 E

11. Calcular las áreas de las regiones
Solución:
A=b.h
22 A=39.22
A=858
34

12. Calcular las áreas de las regiones
Solución:
24 22 A=b.h
A=24.22
A=528

13. Calcular las áreas de las regiones
h(b1 b 2)
A
20
2
A 16.(20 40)
16 2
A 16.(60)
40 2
A 480

14. Calcular las áreas de las regiones
Calculamos el área de ADC
1.41 25
D A( ADC) .
2 2
A( ADC) 256,25
A C
Debido de ∆(ADC)~∆(ABC) por
criterio LAL, entonces el área de la
región viene dada por:
B ∆(ADC)+∆(ABC)
256,25+256,25=512,5
Entonces el área de las regiones es
512,5

15. Calcular el área de la región sombreada
Calculamos el área de (∆AEG)
A D 5.1 5
A( AEG) 25
2 2
5
Ahora calculamos el área
G (∆DHF)
H
F 3.5 15
E 1 3 A( DHF ) 7,5
2 2
4
B 5 C
α

16. Calcular el área de la región sombreada
Calculamos también :
A D A(BGHC)
A(BGHC)= 5.4=20
5 Entonces el área de la región
sombreada es :
G H
F A= A(∆AEG)+A(∆ DHF)+A(BGHC)
E 1 3 A= 2,5+7,5+20
4 A=30
B 5 C
α

17. Área de polígono regulares
Encuentre la apotema y el área de cada
polígono regular dado
Solución.
C A=1/2 .a.n.s
apotema longitud
Nº de
lados
A=1/2ª.30
A B
10
α

18. Área de polígono regulares
Por teorema de Pitágoras
calculamos la altura de triángulo
a 2 10 2 5 2
a 2 100 25
a 2 75
C a 5. 3
Entonces el área del triángulo
ABC
a A( A B C)
10.5 3
25 3
2
Y la apotenusa la sacamos del
A B
10 despeje de:
1
A .a . p
2
2A 2.25 3 50 3 5
a a 3
p 30 30 3

19. Área de polígono regulares
1
a .a.n.s
El área de un hexágono regular es 50 3 2
p n.s
p 12cm
¿cuál es el perímetro y el apotema?
1
A .a. p
2
1
50 3 .a.12cm
2
2.50. 3
a
12cm
100 3
a
12
50
a 3
6
25
a 3
3