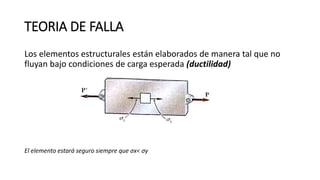
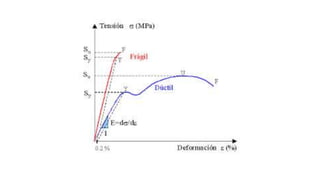
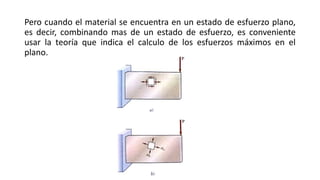
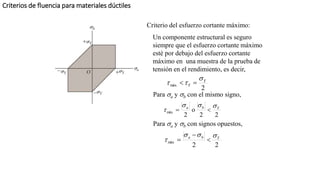
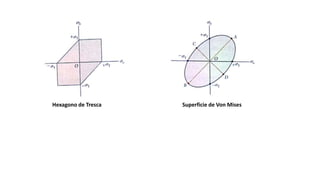
Este documento presenta diferentes criterios de falla para materiales dúctiles sometidos a esfuerzos. Explica que los elementos estructurales deben diseñarse para no fallar bajo las cargas esperadas y que el criterio del esfuerzo máximo puede usarse para un solo estado de esfuerzo. Sin embargo, cuando hay más de un estado de esfuerzo se deben usar criterios como el esfuerzo cortante máximo, la máxima energía de distorsión o los hexágonos de Tresca y Von Mises para predecir la falla. También

1. UNIDAD I
TRANSFORMACION DE ESFUERZOS
Dpto. de estructuras, UNI FTC
Tema: Criterios de falla

3. TEORIA DE FALLA
Los elementos estructurales están elaborados de manera tal que no
fluyan bajo condiciones de carga esperada (ductilidad)
El elemento estará seguro siempre que σx< σy

5. Pero cuando el material se encuentra en un estado de esfuerzo plano,
es decir, combinando mas de un estado de esfuerzo, es conveniente
usar la teoría que indica el calculo de los esfuerzos máximos en el
plano.

6. Criterios de fluencia para materiales dúctiles
Criterio del esfuerzo cortante máximo:
Un componente estructural es seguro
siempre que el esfuerzo cortante máximo
esté por debajo del esfuerzo cortante
máximo en una muestra de la prueba de
tensión en el rendimiento, es decir,
2
máx
Y
Y


 

Para a y b con el mismo signo,
2
2
o
2
máx
Y
b
a 


 

Para a y b con signos opuestos,
2
2
máx
Y
b
a 


 



7. Hexagono de Tresca Superficie de Von Mises

8. Criterios de fluencia para materiales dúctiles
Criterio de la máxima energía de distorsión:
Un componente estructural es seguro
siempre y cuando la energía de distorsión
por unidad de volumen sea inferior a la que
se produce en una muestra de prueba de
tensión en el rendimiento.
   
2
2
2
2
2
2
2
0
0
6
1
6
1
Y
b
b
a
a
Y
Y
b
b
a
a
Y
d
G
G
u
u






















9. EJERCICIO 1

11. EJERCICIO 2
Para el estado de esfuerzo plano mostrado, realice la transformación de
los esfuerzos además de el factor de seguridad asociado a los criterios
de falla de tresca y Von Mises. Considere un esfuerzo de fluencia del
material de 250MPa.

12. Ejercicio 3
La viga mostrada en la figura se encuentra sometida al esquema
de carga mostrada, determine los esfuerzos en el punto P del perfil
mostrado. Considere I = 67.4e-4 m4. Considere Fy del acero, 345MPa.