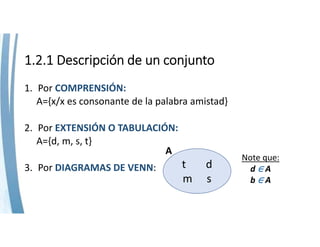
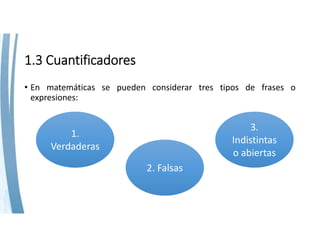
Este documento presenta conceptos básicos sobre conjuntos. Explica qué es un conjunto, cómo se pueden describir y representar conjuntos, la cardinalidad de un conjunto, y tipos de conjuntos como vacíos, unitarios, finitos e infinitos. También introduce nociones sobre cuantificadores, símbolos de la teoría de conjuntos, subconjuntos, relaciones entre conjuntos, operaciones entre conjuntos y propiedades de dichas operaciones. Finalmente incluye ejercicios de aplicación de los conceptos.

1. UNIVERSIDAD DE GUAYAQUIL
FACULTAD DE CIENCIAS ECONÓMICAS
Tic para la toma de decisiones
Computación II
CONJUNTOS
Docente: Ing. Francisco Arias Larrea, MBA.

2. Contenido
1.1. Pseudocódigo
1.2. Conjunto
1.3. Tablas de verdad
1.4. Lógica matemática
1.5. Proposiciones
1.6. Algoritmo (realizable, comprensible, preciso)
1.7. Resolución de problemas (comprender, planear, analizar soluciones)
1.8. Diagrama de Flujo
1.9. Aplicaciones para el aprendizaje de algoritmos
1.10. Practicas de la Unidad

3. 1.2. Conjunto
Nociones básicas

4. 1.2. Conjunto ‐ Nociones básicas
• Un conjunto es una colección de objetos.
• Se usan letras mayúsculas como A, B, X para denotar conjuntos
• Se usan letras minúsculas como a, b, c, x para denotar los objetos.

5. 1.2. Conjunto ‐ Nociones básicas
• Un objeto a que pertenece a un conjunto X se dice que es un miembro o
elemento de X.
Escribiremos a ∈ X para indicar que a es un elemento del conjunto X.
• En caso que a no pertenezca a X escribiremos a ∉ X.
• La expresión a ∈ X puede leerse
de varias maneras equivalentes:
• a pertenece a X,
• a es un elemento de X,
• a está en X.

6. 1.2.1 Descripción de un conjunto
• La descripción de un conjunto se puede realizar de las
siguientes maneras:
1. Por COMPRENSIÓN, para referirnos a alguna característica
de los elementos
2. Por EXTENSIÓN o TABULACIÓN, cuando se listan todos los
elementos.
3. Por medio de DIAGRAMAS DE VENN, cuando se desea
representarlo gráficamente.

7. 1.2.1 Descripción de un conjunto
1. Por COMPRENSIÓN:
A={x/x es consonante de la palabra amistad}
2. Por EXTENSIÓN O TABULACIÓN:
A={d, m, s, t}
3. Por DIAGRAMAS DE VENN: t d
m s
A
Note que:
d ∈ A
b ∈ A

8. 1.2.2 Cardinalidad ‐ Definición
• Es importante conocer el número de elementos con los que está
compuesto un conjunto, esta cantidad recibe el nombre de
cardinalidad, la cual se define como:
Es la cantidad de elementos de un conjunto A.
Se denota por el símbolo N(A).
A={x/x es un dígito impar en el sistema de numeración decimal}
N(A) = 5, porque A = {1, 3, 5, 7, 9}
Ejemplo:

9. 1.2.3 Conjuntos relevantes
• Sea A un conjunto, se pueden dar los siguientes casos:
• A es VACÍO si no tiene elementos
CONJUNTO ES SÍMBOLO/REPRESENTACIÓN
A VACÍO ∅. N(A) = 0
A UNITARIO N(A) = 1
A FINITO CANTIDAD FINITA DE ELEMENTOS
A INFINITO CANTIDAD INFINITA DE ELEMENTOS
A
REFERENCIAL
O UNIVERSO
Re o U

10. Ejemplo de conjuntos relevantes

11. 1.3 Cuantificadores
• En matemáticas se pueden considerar tres tipos de frases o
expresiones:
1.
Verdaderas
1.
Verdaderas
2. Falsas2. Falsas
3.
Indistintas
o abiertas
3.
Indistintas
o abiertas

12. Ejemplos
1. Expresiones que son
proposiciones
verdaderas
5 + 3 = 8
2 < 6
2. Expresiones que
son propiciaciones
falsas
5 + 3 = 10
2 > 6
3. Expresiones
indistintas o abiertas
5x + 3y = 8
2x < 6

13. • Las expresiones antes vistas, pueden ser expresiones
verdaderas, falsas o indistintas o abiertas, dependiendo de
las sustitución que se hagan para x o y.
• Se desea aplicar ahora el estudio de la lógica a las
expresiones abiertas y para ello, se debe restringir o
cuantificar la variable, diciendo que la expresión es
verdadera para todos o algunos de sus valores posibles.
• Para ello se hace necesario aplicar un símbolo que permita
obtener proposiciones a partir de expresiones abiertas.
• A continuación se definirán los cuantificadores Universal y
Existencial.

15. Ejemplo de Cuantificadores
• Estas expresiones si pueden ser calificadas como verdaderas o falsas,
lo cual las convierte en proposiciones de acuerdo a la definición de
proposición.
• Vemos que en el caso de una expresión abierta con cuantificadores,
se sugiere o se supone algún conjunto referencial, del cual se
obtienen los valores posibles de la variable.

16. Símbolos de la Teoría de
Conjuntos

17. Símbolos utilizados en la Teoría de conjuntos
• Los símbolos que frecuentemente son utilizados para hablar
de conjuntos son los siguientes: para todo ( ), existe ( ),
igual o identidad (=), variables u objetos individuales (x1, x2,
x3….). Símbolo de pertenencia ( ), no pertenencia ( ). En
general la negación particulares símbolos, se identificará con
una raya que lo atraviesa desde arriba, hasta abajo, por la
mitad.

20. Practicamos un poco con estos símbolos.
• Consideramos el conjunto de estudiantes de la UG. A este conjunto lo
podemos denominar U.
• Consideramos el conjunto de estudiantes de alguna asignatura de
Computación a la UG. Denominamos C este conjunto. Este conjunto
se puede definir así:
C ={x∈U / x cursa alguna asignatura de computación}
que se lee, C es el conjunto de los x pertenecientes a U tales que x
cursa una asignatura de Computación.
• Evidentemente C ⊂ U , pero U ⊄ C.
• Quienes leen este mensaje son la prueba que C ≠ ∅, es decir, que
C no es un conjunto vacío.

21. • Podemos decir, además que
∀x x ∈ C ⇒ x es un estudiante universitario
es decir, que para todo x que pertenezca a C, implica que x es un
estudiante universitario.
• También se puede afirmar que
∀x x ∈ C ⇔ x esta cursando una asignatura de computación
evidentemente, todo x que pertenezca a C cursa una asignatura de
Computación y, por lo demás, si x cursa una asignatura de Computación,
implica que pertenece al conjunto C.
• Se ha de ir con cuidado con la implicación. Es cierto que,
∀x x ∈ C ⇒ x ∈ U
• Ahora bien, la implicación contraria no es cierta (∀x x ∈ C ⇐ x ∈ U), porque
puede haber alumnos de la UG que no cursen asignaturas computación.

22. Subconjuntos

24. • La proposición (x ) es falsa, porque no existen
elementos que pertenezcan al conjunto vacío.
• Adicionalmente, la proposición 0p es siempre
verdadera, sin importar el valor de verdad de la
proposición p, con lo que podemos concluir que:
[(x )(x A)] ≡ 1, es decir que A. El conjunto
vacío es subconjunto de cualquier conjunto.
• Si realizáramos un análisis similar, podríamos concluir
también que todo conjunto es subconjunto de sí mismo:
A A.

25. Relaciones entre
conjuntos

26. Usando las definiciones de la lógica proposicional, se tiene que:

27. Operaciones entre conjuntos

28. • Es posible realizar
operaciones entre
conjuntos para
formar otros nuevos.
• Las operaciones más
utilizadas son:
Unión
Intersección
Diferencia
Diferencia simétrica
Complementación

29. UNIÓN ENTRE CONJUNTOS

30. INTERSECCIÓN ENTRE CONJUNTOS

31. DIFERENCIA ENTRE CONJUNTOS

32. DIFERENCIA SIMÉTRICA ENTRE CONJUNTOS

33. COMPLEMENTACIÓN ENTRE CONJUNTOS

34. Propiedades
de las
operaciones
entre
conjuntos

35. Propiedades de las operaciones entre
conjuntos
• Los operaciones entre conjuntos y algunas de sus más importantes
propiedades se incluyen en las denominadas Leyes del Álgebra de
Conjuntos. A continuación se presentan las de uso más frecuente:

36. Ejercicios

37. Ejercicios

38. Ejercicios

39. Ejercicios

40. Ejercicios

41. Ejercicios

42. Ejercicios

43. Ejercicios