Cuadernillo matemática ingreso2013

Para el ingreso a las carreras:
Contador Público Nacional – Licenciatura en Administración
– Ciclo General en Ciencias Económicas – Profesorado en
Ciencias Económicas – Profesorado en Matemática –
Licenciatura en Matemática
Facultad de Economía y Administración
Universidad Nacional del Comahue.
Año 2013.
Este cuadernillo está basado en el material realizado por las profesoras Valeria Castaño y Silvia Rodríguez y
modificado por el grupo de Docentes Tutores de la FaEA

Curso de Nivelación en Matemática
1
¡Bienvenidos!
Estos apuntes han sido pensados para ayudarte a recuperar y consolidar los
conocimientos matemáticos que seguramente adquiriste en el nivel medio, y que son la base
para afianzar otros más complejos relacionados con la profesión que elegiste.
Para que podamos alcanzar este propósito es necesario que emprendas esta nueva etapa
con responsabilidad y compromiso, sabiendo que nada es posible sin esfuerzo y que nada
es tan difícil, incomprensible o inalcanzable como parece, sólo se necesita constancia,
paciencia y horas de estudio.
Te sugerimos la lectura de este cuadernillo previa a la asistencia al curso. En
clase se desarrollarán algunos ejemplos, se trabajará en grupo y se podrán consultar las dudas
que hayan tenido en la resolución de los problemas.
Son objetivos de este curso que te habitúes a los tiempos disponibles en la Universidad
para estudiar un tema, que siempre son breves, y que fortalezcas tu capacidad de resolver
problemas de la manera más conveniente y en el menor tiempo posible, por lo que esperamos
que aproveches los horarios de clase para completar aquellos ejercicios en que hayas tenido
inconvenientes y verifiques los resultados que obtuviste, y no para comenzar a resolverlos
recién en la clase.
Cada persona tiene una modalidad de estudio, de trabajo. Sin embargo te recomendamos
que sigas el orden en que están presentados los temas y que trates de resolver la guía de
ejercicios de cada uno de ellos. Es posible que aparezcan dificultades, no te desanimes, volvé a
intentarlo. Si aún no llegás a la solución, anotá las dudas y buscá ayuda, un profesor o un
compañero pueden brindártela. No te desanimes, seguí adelante, todo es posible, sólo hay que
intentarlo.

2
IINNDDIICCEE::
Conjuntos Numéricos…………………………………………………. 3
Polinomios……………………………………………………………… 26
Expresiones Algebraicas Racionales………………………………. 44
Ecuaciones e Inecuaciones…………………………………………… 52
Funciones………………………………………………………………. 68
Trigonometría………………………………………………..………… 85
Bibliografía…………………………………………………………….. 94

3
CONJUNTOS NUMÉRICOS
La noción de número es tan antigua como el hombre mismo ya que son necesarios para resolver
situaciones de la vida diaria. Por ejemplo, usamos números para contar una determinada
cantidad de elementos (existen siete notas musicales, 9 planetas, etc.), para establecer un orden
entre ciertas cosas (el tercer mes del año, el cuarto hijo, etc.), para establecer medidas (3,2
metros, 5,7 kg, –4ºC, etc.), etc.
Problema 1: Escribir los dígitos 1, 2, 3, 4, 5, 6, 7, 8, 9 en las casillas de forma que la suma de
los tres números de cada fila, de cada columna, y de las dos diagonales, dé siempre el mismo
resultado. A esta distribución se le llama cuadrado mágico.
4 2
5
8
Podemos afirmar que todos los números que utilizamos para resolver este problema son
números naturales.
El conjunto de los números naturales está formado por aquellos que se utilizan para contar. Se
los designa con la letra ℕ y se representan:
ℕ = 1, 2, 3, 4, 5, …
Es un conjunto que tiene infinitos elementos pues si bien tiene primer elemento, el 1 que es el
menor de todos, no tiene último elemento ya que es suficiente con sumar 1 a un número para
obtener otro mayor. Así, podemos afirmar también que es un conjunto ordenado, por lo que
podemos representarlos sobre una recta de la siguiente manera:
Observación:
 Todo número natural 𝑛 tiene su sucesor 𝑛 + 1 y excepto el 1 también tiene su antecesor,
𝑛 − 1.
 Siempre que se sumen dos números naturales se obtendrá otro número natural mientras
que muchas veces, no sucede lo mismo si se restan.
1 2 3 4 5 6

4
Pregunta: ¿Es posible encontrar un número que al restárselo a 32 dé por resultado 38?
Si lo traducimos al lenguaje algebraico: 32 − 𝑥 = 38, donde 𝑥 representa al número buscado.
Es imposible encontrar un número natural que cumpla con estas condiciones. Decimos que esta
ecuación no tiene solución en el conjunto de los números naturales y lo escribimos así , 𝑆 = ∅ .
Para encontrar una solución a esta ecuación debemos buscarla en el conjunto de los números
enteros, que se simboliza ℞ y está formado por los números naturales, el cero y los opuestos de
los números naturales.
℞ = … , −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, … = ℕ−
∪ 0 ∪ ℕ
El conjunto de los números enteros es un conjunto infinito que no tiene ni primer ni último
elemento, por lo que todo elemento de este conjunto tiene su siguiente 𝑛 + 1 y su anterior,
𝑛 − 1.
Entre dos números enteros 𝑎 y 𝑏 hay siempre una cantidad finita de números enteros, esta
propiedad se conoce con el nombre de discretitud.
Observación:
 Al número – 𝑎 se lo llama opuesto de 𝑎. Dos números opuestos son aquellos que se
encuentran a la misma distancia (en unidades) del cero. Uno positivo y uno negativo, con
excepción del cero, cuyo opuesto es él mismo.
Por ejemplo: Si 𝑎 = 4 , su opuesto −𝑎 es −4
Si 𝑎 = −11, su opuesto – 𝑎 es − −11 = 11
 El valor absoluto o módulo de un número 𝑎 se define como la distancia de éste al cero.
-1 es el opuesto de 1
2 es el opuesto de -2
-3 -2 -1 0 1 2 3
3 unidades
3 3
1 unidad
1 1 
-3 -2 -1 0 1 2 3

5
 Dos números opuestos tienen igual distancia al cero, es decir, tienen el mismo valor
absoluto, es decir, 𝑎 = −𝑎 .
Actividad 1:
a) En la siguiente recta numérica están ubicados 0, 1 y 𝑎 .
¿Dónde ubicarías los números 𝑎 + 1, −𝑎 y −𝑎 + 1?
b) En la siguiente recta están ubicados los números 0 y 𝑎.
¿Dónde ubicarías al número – 𝑎 ?
Observación:
 La suma de dos números enteros da siempre un número entero.
 La multiplicación de dos números enteros da siempre un número entero.
¿Pasará lo mismo con la división?
4 ∶ 2 = 2 ya que 2 ∙ 2 = 4
−6 ∶ 3 = −2 ya que 3 ∙ −2 = −6
En general 𝑎 ∶ 𝑏 = 𝑐 , 𝑏 ≠ 0 si se verifica que 𝑏 ∙ 𝑐 = 𝑎
Pero, ¿Cuál será el resultado de 4 ∶ 3? Debemos pensar en un número entero tal que al
multiplicarlo por 3 dé como resultado 4. ¿Hay algún número entero que cumpla con esta
condición?
Para resolver esta situación habrá que introducir otro conjunto numérico, el conjunto de los
números racionales al que denotaremos con la letra ℚ.
Un número racional es el cociente (división) de dos números enteros 𝑚 y 𝑛, siendo 𝑛 ≠ 0. Por lo
tanto: ℚ =
𝑚
𝑛
, 𝑚, 𝑛 ∈ ℞ , 𝑛 ≠ 0 , donde 𝑚 es el numerador y 𝑛 el denominador. Notemos que
℞ ⊂ ℚ.
De la definición de número racional surge que todo número entero es racional, pues podemos
considerar al entero como un racional de denominador 1.
Por ejemplo: −3 =
−3
1
, donde −3 ∈ ℞, 1 ∈ ℞ y 1 ≠ 0 .
Podemos preguntarnos: ¿Por qué se excluye al 0 del denominador en la definición?
Representemos en la recta numérica algunos números racionales:
0 1 a
a 0
−1
3
0 1
4
3

6
Actividad 2: En cada caso, ubicar en la recta numérica los números racionales indicados.
a) −
4
3
b)
3
8
𝑦 − 1
c) 1 𝑦 −
1
3
d) 0 y
1
2
Actividad 3:
a) ¿Qué número representa p?
b) Encontrar las fracciones irreducibles que representan a y b.
Actividad 4: Ahora analicemos algunas expresiones decimales:
 0,3 es la expresión decimal de un número racional porque 0,3 =
3
10
y 3 y 10 son números
enteros.
 0, 5 = 0,555 …. es la expresión decimal de un número racional porque 0, 5 =
5
9
y 5 y 9 son
números enteros.
 0,15 = 0,1555 … … es la expresión decimal de un número racional porque 0,15 =
14
90
y 14
y 90 son números enteros.
Estos tres últimos ejemplos muestran los tres tipos diferentes de expresiones decimales que
puede tener un número racional:
 Expresión decimal finita: 0,3 ; −0,107 ; 12,001
 Expresión decimal periódica pura: 0, 23 = 0,2323 … ; 7, 20 = 7,202020 ….
 Expresión decimal periódica mixta: 0,15 = 0,1555 …. ; −5,2513 = −5,251313 … ..
0 2
3
0
−
3
4
0
−
1
2
1
8
−
2
3
3
2
1
2
𝑎+
7
4
a b
−
1
2
5
4
p

7
Todo número racional puede escribirse como una expresión decimal cuya parte decimal puede
tener un número finito de cifras o puede tener un número infinito de cifras pero periódicas,
pura o mixta.
Supongamos que nos dan el número decimal 23,35. Es una expresión decimal periódica mixta,
así que ya sabemos que es un número racional y por lo tanto se tiene que poder expresar como
una fracción (cociente de dos enteros). ¿Qué fracción es?
Para hallar esta fracción, existe una regla muy simple que podemos resumir así:
periódicasnodecimalescifrascomo0y tantosperiódicasdecimalescifrascomo9tantos
expresión)ladeperiódicasnocifras(lasexpresión)ladecifraslas(todas 
Aplicando esta regla al ejemplo, obtenemos: 23,35 =
2335−233
90
=
2102
90
Y simplificando la fracción obtenemos: 23,35 =
1051
45
Otro ejemplo: 32,1427 =
321427−321
9990
=
321106
9990
=
160553
4995
Observación:
 Siempre podemos verificar si la fracción que obtuvimos es correcta realizando la división y
verificando que el resultado coincide con la expresión decimal que teníamos.

8
Recordemos como realizábamos las cuatro operaciones fundamentales:
Adición y Sustracción Multiplicación División
Igual denominador:
a c a c
b b b

  , b 0
a c a c
b b b

 
Distinto denominador:
Cuando las fracciones tienen
distinto denominador se procede
a reemplazar a cada una de estas
por otras, respectivamente
equivalentes a las dadas, con
igual denominador. Luego se
suman o se restan como en el
caso anterior.
Ejemplo:
5 7 10 6 21
1
3 2 6 6 6
10 6 21 5
6 6
     
 
  
.
.
.
a c a c
b d b d
 , 0b d
Se multiplican los
numeradores y los
denominadores entre sí.
: .
a c a d
b d b c
 o
.
:
.
a c a d
b d b c

Ejemplo:
3 2 3 7 21
: .
5 7 5 2 10
    
 3 .73 2 21
:
5 7 5.2 10

   
Inverso multiplicativo:
Dos números racionales
(distintos del cero) son
inversos multiplicativos si
el numerador de uno es el
denominador del otro y
viceversa. De tal forma que
la multiplicación de ambos
es 1.
3 2 3 2 6
y donde . 1
2 3 2 3 6
 
Formalmente Definimos el
inverso de un número a  0
como el número racional
que multiplicado por a nos
da 1, es decir,
1
1a
a
 
 El inverso de
27
2
a  
es
1 2
27a
  pues
27 2
1
2 27
 
    
 

9
Actividad 5: Completar el siguiente triángulo numérico con las fracciones que faltan.
Observación:
 Veamos que estas expresiones son equivalentes:
a)
3
5
= 3 ∙
1
5
=
1
5
+
1
5
+
1
5
b) −
3
8
=
−3
8
=
3
−8
Recordemos que si necesitamos buscar fracciones equivalentes a otras dadas para realizar una
suma es aconsejable buscar el mínimo común múltiplo (m.c.m.) entre los denominadores.
Actividad 6:
1) En una fábrica se oye, cada 20 segundos, el golpe de un martillo y cada 45 segundos, el
escape de la presión de una válvula. Si se acaban de oír ambos ruidos simultáneamente ¿cuánto
tiempo transcurrirá hasta que vuelvan a coincidir?
2) Calcular el mínimo común múltiplo de los siguientes números:
a) 15 y 20 b) 30 y 45 c) 4, 6 y 10 d) 12 y 18
3) Resolver las siguientes sumas algebraicas:
a)
7
30
+
4
5
−
8
45
b)
11
4
−
5
6
+
1
18
−
9
10
Actividad 7: Si 𝑛 es un número racional, ¿es cierto que no existe ningún otro número racional
entre 𝑛 y 𝑛 + 1?
Si 𝑛 es un número entero, 𝑛 + 1 es el entero siguiente y no existe otro número entero entre
ellos. Pero, a diferencia del conjunto de los números enteros, en ℚ no tiene sentido hablar de
siguiente ni de anterior. Por ejemplo, si 𝑛 =
1
2
no podemos afirmar que
1
2
+ 1 =
3
2
sea su sucesor
inmediato pues existe el 1 o el
3
4
que están entre ellos y podríamos seguir encontrando otros
números racionales que cumplan con la misma condición.
1
1/2 1/2
1/3 1/31/6
1/4 1/41/12 1/12
1/301/20 1/201/5
1/6
1/7
1/30 1/60 1/60

10
Esta propiedad se expresa diciendo que el conjunto ℚ es un conjunto denso, en contraposición
a los naturales ℕ y los enteros ℞ que, como ya dijimos, son conjuntos discretos.
Problema: ¿Cuáles son las medidas de los catetos de un triángulo rectángulo isósceles si se
sabe que su área es 6,5 𝑐𝑚2
?
Como el triángulo es rectángulo isósceles, sus catetos son iguales por lo que el área que es de
6,5 cm2
queda expresada con la siguiente ecuación:
𝑥 ∙ 𝑥
2
= 6,5 ⟺ 𝑥2
= 13
Esta ecuación no tiene solución en el conjunto de los números racionales ℚ, porque no existe
ningún número racional que elevado al cuadrado dé por resultado 13.
Aparece entonces un nuevo conjunto numérico, el de los números irracionales que se simboliza
con 𝕀. Los elementos de este conjunto tienen desarrollo decimal infinito no periódico.
El lado del triángulo anterior mide 13 y es un número irracional. Otros números irracionales
son:
6,12123123412345….
𝜋 = 3,14159254 …
−15,161718192021 …
7
3
Los números irracionales también tienen su ubicación en la recta numérica.
El conjunto formado por los números racionales y por los irracionales se llama conjunto de los
números reales que se simboliza ℝ.
Observemos que entre dos números racionales, 𝑎 y 𝑏 , 𝑎 < 𝑏, existe el racional
𝑎+𝑏
2
que
verifica: 𝑎 <
𝑎+𝑏
2
< 𝑏
Conclusión: entre dos racionales distintos a y b existen infinitos números racionales.
𝑥
𝑥
x

11
ℝ = ℚ ∪ 𝕀
Los números reales tienen la propiedad de llenar por completo la recta numérica, por eso se la
llama recta real.
Dado un origen y una unidad, a cada punto de la recta le corresponde un número real y, a cada
número real, le corresponde un punto de la recta.
PROPIEDADES DE LAS OPERACIONES EN ℝ
Suma y producto
Las operaciones de suma y producto definidas en ℝ cumplen ciertas propiedades. Veamos
algunas de ellas:
Sean 𝑎, 𝑏 y 𝑐 números reales cualesquiera.
Propiedades
de la Suma del Producto
Ley de cierre
a b  ℝ a b  ℝ
Asociativa    a b c a b c     *    a b c a b c     *
Conmutativa a b b a   a b b a  
Existencia de elemento neutro
Es el 0:
0 0a a a   
Es el 1:
1 1a a a   
Existencia de inverso
Es el opuesto aditivo:
( ) ( ) 0a a a a     
Es el inverso multiplicativo:
1 1
1 0a a si a
a a
    
Distributiva del producto con
respecto a la suma
 a b c a c b c     
ℝ
ℚ
ℕ℞
𝕀
ℕ ⊂ ℞ ⊂ ℚ ⊂ ℝ
ℚ ∪ 𝕀 = ℝ

12
Observación:
*La propiedad asociativa nos permite prescindir del uso de paréntesis y escribir simplemente
𝑎 + 𝑏 + 𝑐 ó 𝑎 ∙ 𝑏 ∙ 𝑐 .
Actividad 8: Decir si las siguientes afirmaciones son verdaderas o falsas. En caso de ser
verdaderas, mencionar las propiedades utilizadas.
a)
1
3
∙ 5 + 4 =
4
3
+
5
3
b) −2 ∙
8
9
− 5 = −2 ∙
8
9
− 5
c) 2 + 𝑐 = 𝑐 + 2
d) 3 + 8 ∙ −9 = 3 + 8 ∙ 3 + −9
e)
1
𝑎
∙ 𝑎 = 1, ∀𝑎 ∈ 𝑅
f) Existe un número real 𝑥 para el cual
5
𝜋
+ 𝑥 = 0
Potenciación
Si 𝑎 es un número real y 𝑛 es un número natural, entonces decimos que 𝑎 𝑛
se obtiene
multiplicando 𝑛 veces el factor 𝑎, es decir:
...n
n veces
a a a a   
Ejemplo: 𝑎3
= 𝑎 ∙ 𝑎 ∙ 𝑎
Decimos entonces que 𝑎 𝑛
es una potencia que tiene 𝑎 como base y 𝑛 como exponente.
Extendemos la definición para exponentes enteros definiendo, para 𝑎 ≠ 0:
𝑎0
= 1
𝑎−𝑛
= 𝑎−1 𝑛
, 𝑛 ∈ ℕ
Actividad 9: Decir si los siguientes enunciados son verdaderos o falsos:
a) 28
= 22
∙ 26
= 25
∙ 23
f) −32
= −3 2
b) 8 + 3 2
= 82
+ 32
g) 54
= 45
c) 8 ∙ 3 2
= 82
∙ 32
h)
3
4
−2
=
4−2
3−2
d) 23 2
= 25
i) 5−2
= −10
e) 23 2
= 26
La actividad anterior ejemplifica algunas de las siguientes propiedades de la potencia:

13
Sean 𝑎, 𝑏 números reales distintos de 0 y sean 𝑚, 𝑛 números enteros.
Propiedades de la Potencia
Distributiva con respecto al producto 𝑎 ∙ 𝑏 𝑚
= 𝑎 𝑚
∙ 𝑏 𝑚
Distributiva con respecto a la división
𝑎
𝑏
𝑚
=
𝑎 𝑚
𝑏 𝑚
Producto de potencias de igual base 𝑎 𝑛
∙ 𝑎 𝑚
= 𝑎 𝑛+𝑚
División de potencias de igual base
𝑎 𝑛
𝑎 𝑚 = 𝑎 𝑛−𝑚
Potencia de potencia 𝑎 𝑛 𝑚
= 𝑎 𝑛∙𝑚
Como se vió en el ejercicio anterior la potencia no es distributiva con respecto a la suma ni a la
resta.
Actividad 10: ¿Qué sucede si a un número negativo lo elevamos a una potencia par? ¿Cuál es
el signo del resultado?
Radicación
Para los enteros positivos 𝑛 ya se ha definido la 𝑛-ésima potencia de 𝑏, a saber, 𝑏 𝑛
. Ahora
vamos a utilizar la ecuación 𝑎 = 𝑏 𝑛
para definir la 𝑛-ésima raíz de 𝑎.
La notación de la raíz cuadrada de 49 es 49. Su valor es
7 porque 72
= 49 y 7 > 0. Aun cuando −7 2
= 49, el
símbolo 49 se usa sólo con +7 y no con −7, así que se
tendrá un solo valor de 49. Claro que siempre es posible
escribir − 49 si se desea el valor negativo −7. Podemos
observar que −49 no tiene una raíz cuadrada real ya que
𝑏2
> 0 para todo número real 𝑏, por lo que 𝑏2
= −49 no
tiene solución en el conjunto de los números reales. En
general, la raíz cuadrada de 𝑎 se define como sigue, a
veces recibe el nombre de raíz cuadrada principal de 𝑎.
Si 𝑎 es un número real positivo, 𝑎 = 𝑏 si y sólo si 𝑎 = 𝑏2
y 𝑏 > 0
Además, 0 = 0.
Ejemplo: 25 = 5 , pues 52
= 25 (no es −5 ni ±5)
En el caso de las raíces cúbicas se puede utilizar tanto números positivos como negativos, así
como el cero. Por ejemplo, 23
= 8 y −5 3
= −125

14
Se puede decir entonces que,
Si 𝑎 y 𝑏 son números reales cualesquiera, 𝑎3
= 𝑏 si y sólo si 𝑎 = 𝑏3
En particular, 0
3
= 0
Ejemplo: 343
3
= 7 pues 73
= 343
−1728
3
= −12 pues −12 3
= −1728
Se puede ver que existe una diferencia básica entre las raíces cuadradas y las raíces cúbicas.
Las raíces cuadradas están definidas sólo para los números reales positivos y el cero. Las raíces
cúbicas están definidas para cualquier número real.
Lo mismo sucede con los enteros positivos mayores 𝑛: la distinción fundamental surge de si 𝑛 es
par o impar.
 Si 𝑛 es un entero positivo par y 𝑎 y 𝑏 son números reales positivos tales que 𝑎 = 𝑏 𝑛
,
entonces se escribe 𝑎
𝑛
= 𝑏.
 Si 𝑛 es un entero positivo impar y 𝑎 y 𝑏 son números reales tales que 𝑎 = 𝑏 𝑛
entonces se
escribe 𝑎𝑛
= 𝑏.
 En cualquiera de los dos casos, 0
𝑛
= 0. Además, 𝑎
𝑛
se llama raíz 𝑛 -énesima de 𝑎.
El símbolo 𝑎 se utiliza sólo para representar 𝑎2
.
Observaciones:
 𝑎
𝑛
recibe el nombre de 𝑛 -énesima raíz principal de 𝑎 para indicar que 𝑎
𝑛
se define
positivo si 𝑎 > 0.
 El número 𝑎 es el radicando, es el signo radical, 𝑛 es el índice del radical y 𝑎𝑛
es la
expresión radical o raíz 𝑛 -énesima de 𝑎.
Veamos ahora las propiedades de la radicación, las cuales son análogas a las de la potenciación.
Sean 𝑎𝑎 y 𝑏 𝑏números reales positivos y 𝑛 𝑛, 𝑚 𝑚números naturales:
Propiedades de la Radicación
Distributiva con respecto al producto 𝑎 ∙ 𝑏
𝑛
= 𝑎𝑛
∙ 𝑏
𝑛
Distributiva con respecto a la división
𝑎
𝑏
𝑛
=
𝑎𝑛
𝑏
𝑛
Raíz de raíz 𝑎𝑚𝑛
= 𝑎𝑛∙𝑚

15
Actividad 11:
1) ¿Es posible aplicar la propiedad distributiva de la radicación respecto a la suma o a la
resta? Proponer ejemplos.
2) ¿Qué sucede al aplicar la propiedad distributiva al siguiente radical: −4 ∙ −16 ?
SIMPLIFICACIÓN DE RADICALES
Actividad 12: Efectuar las siguientes operaciones
a) 284
, 24 y 22
b) 32010
, 34 y 32
c) −2 6 y −2 3
Observemos que, en algunos casos se puede dividir el índice de la raíz y el exponente del
radicando por un mismo número sin alterar el resultado. A esta propiedad la llamaremos
simplificación de radicales.
Si el índice de la raíz es impar se puede simplificar siempre sin tener en cuenta el signo de la
base del radicando. Por ejemplo:
−2 55
= −2 (dividimos índice y exponente por 5)
2
3
217
=
2
3
3
(dividimos índice y exponente por 7)
Si el índice de la raíz es par, sólo se puede simplificar si la base es positiva, ya que si la base
fuera negativa podría presentarse el siguiente caso:
−2 44
= −2 (si dividimos índice y exponente en 4) y en realidad, −2 44
= 16
4
= 2, vemos
que los resultados no coinciden. Por lo tanto:
Cuando el índice es PAR y el radicando es NEGATIVO, NO se puede simplificar...
Notemos que la única diferencia en el resultado es el signo y que las raíces de índice par dan
como resultado siempre un número positivo. Podemos entonces escribir: −2 44
= −2 = 2,
donde el valor absoluto de un número 𝑎se define de la siguiente manera:
𝑎 =
𝑎 𝑠𝑖 𝑎 ≥ 0
−𝑎 𝑠𝑖 𝑎 < 0
Entonces podemos afirmar que:
Si 𝑛𝑛 es impar, 𝑎 𝑛𝑛
= 𝑎 Si 𝑛𝑛 es par, 𝑎 𝑛𝑛
= 𝑎

16
Actividad 13: Descubrir los errores cometidos en el siguiente desarrollo.
9
43
9
25
42
9
25
16
2
4
3
5
)8)(2(
2
1
2
5
3
82
)2(
1
2
2
2
2
8 8
4 8























Potencias de exponente fraccionario
Observemos las siguientes analogías:
23
6
aa  y
23 6
aa  35
15
aa  y
35 15
aa 
Estos ejemplos nos inducen a adoptar la siguiente definición para el caso de potencias de
exponente fraccionario:
𝑎
𝑛
𝑚 = 𝑎 𝑛𝑚
, donde 𝑎 ∈ ℝ+
, 𝑛 ∈ ℞ y 𝑚 ∈ ℕ
Actividad 14: ¿Cuándo es posible calcular una potencia de exponente fraccionario y base
negativa?
Recordemos como operar con radicales…
Adición y Sustracción de términos con radicales
 Radicales expresados como raíces con igual índice y radicando
1. Se extrae factor común de todos los términos en los que aparezca el radical involucrado:
1 2 1 2
5 6 6 6 2 6. 5 2
3 5 3 5
 
       
 
2. Se suman y restan los números racionales:
1 2 76
6. 5 2 6 2
3 5 15
 
     
 
Este es el
resultado!!!

17
 Radicales expresados como raíces con distinto índice y/o radicando
3. Se descompone cada uno de los radicando, en forma de producto. Buscando que aparezca el
menor de los radicandos en todos los términos
8 2 72 2.4 2 2.36    
4. Se aplica propiedad distributiva con respecto al producto
2.4 2 2.36 2. 4 2 2. 36    
5. Se procede a resolver aquellas raíces cuyo resultado es un numero racional
2. 4 2 2. 36 2.2 2 2.6    
6. Se extrae factor común el numero irracional de cada uno de los términos en los cuales aparece
 2.2 2 2.6 2. 2 1 6    
7. Se resuelve la suma algebraica de números racionales
 2. 2 1 6 2.7 7 2   
Observación:
 Si no es posible encontrar como factor común un radical, no se puede resolver la operación
Multiplicación y división con radicales
Para multiplicar o dividir expresiones en las cuales aparecen números irracionales se procede a
agrupar, si existen, mediante la aplicación de propiedades, los números racionales por un lado y los
irracionales por otro.
Luego se procede a resolver las operaciones que correspondan en racionales y/o irracionales.
Ejemplo:
  1 8. 5 8 5
8. 5 : 2. .
20 21 1
2.
20 20
 
   
 

18
….lo cual puede escribirse….
8 5 1 1
. 4. 5 : 4. 5: 4. 100 4.10 40
2 20 201
20
 
      
 
Racionalización de denominadores
Cuando una expresión fraccionaria tiene indicado en el denominador un radical, resulta
ser conveniente modificar tal expresión- sin cambiar su significado-por otra cuyo
denominador sea racional. Este proceso recibe el nombre de racionalización del
denominador.
Trabajaremos únicamente dos casos:
1 Denominador con radical único: Multiplicamos numerador y denominador por un radical
que tenga:
 igual índice que el que figura en el denominador.
 radicando tal que al efectuar el producto de este con el radicando del radical que
existe, resulte una expresión (un número) que tenga como exponente un múltiplo
del índice (al cual pueda calculársele la raíz en racionales).
Ejemplo:
5 5 5 5 57 7 2 7 2 7 2 7 2 7 2 7
5 2
3 35 5 5 5 5 513 13 2 13 2 13 2 15
5 57 3 2 10 2
. . . . .
.
. .
.
x x x x x x x x x x x x
x
x xx x x x x x x
x x x x
      

  
      

2 Denominador de dos términos con uno o ambos con radicales de igual índice:
 Multiplicamos numerador y denominador por el denominador de la expresión
original, cambiando la operación que separa en términos por la inversa de ésta.
Es decir, si los términos aparecían unidos por la operación de la suma, el que uso
para multiplicar debe tener una resta y viceversa.
Para multiplicar y/o dividir
radicales estos deben tener el
mismo índice.

19
 Aplicamos la siguiente propiedad:     2 2
.a b a b a b    .
 Operamos teniendo en cuenta el conjunto numérico al cual pertenecen los
números.
Ejemplo:
 
   
 
   
 
 
 
2 2
15. 5 8 15. 5 8 15. 5 815
5 85 8 5 8 . 5 8 5 8
15. 5 8
5. 5 8
3
  
   
   

  

Actividad 15: Racionalizar los denominadores de las siguientes expresiones.
a)
5 32
8


= b)
43
35
7

= c) 
 53
5
Relaciones de orden en ℝ
Hasta ahora hemos definido ciertas operaciones en los números reales y analizado sus
propiedades. En esta sección lo que haremos es establecer un orden entre dos números reales
cualesquiera.
Dados dos números reales 𝑎𝑎 y 𝑏 𝑏, se tiene sólo uno de los siguientes casos:
 𝑎 < 𝑏 (se lee “ 𝑎𝑎𝑎 es menor que 𝑏 𝑏”, o “ 𝑏𝑏 es mayor que 𝑎𝑎 𝑎”)
 𝑏 < 𝑎 (se lee “ 𝑏𝑏 es menor que 𝑎𝑎 𝑎”, o “ 𝑎𝑎𝑎 es mayor que 𝑏 𝑏”)
 𝑎 = 𝑏 (se lee “ 𝑎𝑎𝑎 es igual a 𝑏 𝑏” o “𝑏 es igual 𝑎 ”)
Ejemplo: −8 < 1 ;
1
0
5
 ; 2 3 .
Observaciones:
 𝑎 < 𝑏 y 𝑏 > 𝑎 son expresiones equivalentes.
 𝑎 ≤ 𝑏 a (se lee “ 𝑎 es menor o igual que 𝑏”) significa que 𝑎 < 𝑏 o bien 𝑎 = 𝑏.
Por ejemplo: 7 ≤ 9 y también 7 ≤ 7.

20
Actividad 16:
a) ¿Cuántos números naturales hay entre −5 y 7?
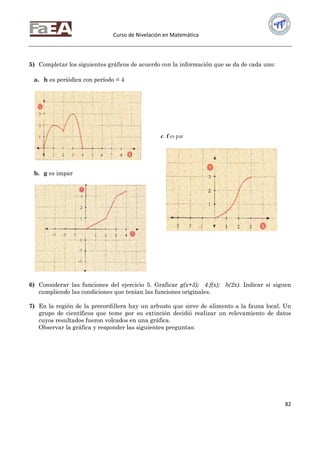
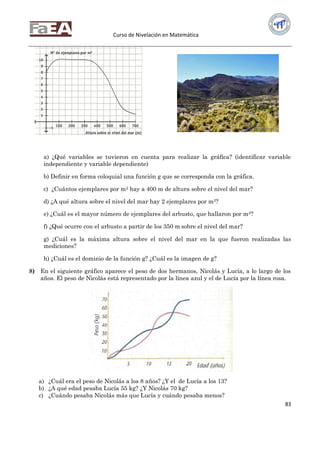
b) ¿Cuántos números enteros hay entre −5 y 7?
c) ¿Cuántos números racionales hay entre −5 y 7? ¿Y cuántos números reales?
INTERVALOS DE NÚMEROS REALES
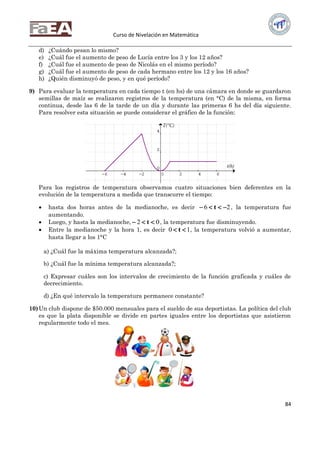
DEFINICIÓN: A un subconjunto de la recta real lo llamamos intervalo si contiene por lo menos
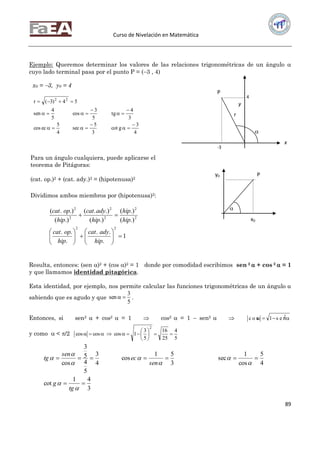
dos números reales y también todos los números reales entre dos de sus elementos.
Ejemplo:
a) A = {x  ℝ / 6 < x < 8} es un intervalo.
b) B = {1, 2, 5, 8} no es un intervalo pues contiene a los números 1 y 2 pero no contiene a
ninguno de los números reales entre 1 y 2 como por ejemplo
3
2
ó 2 .
¿Cómo ubicamos a los números reales en la recta numérica?
Para ello debemos tener en cuenta que dados dos números reales el menor siempre deberá estar
ubicado a la izquierda del mayor. De esta manera:
Clasificación de intervalos:
 Se llama intervalo abierto de extremos a y b al conjunto de los 𝑥 ∈ ℝ que están entre a y
b, sin considerar los extremos a y b. Escribiremos 𝑎, 𝑏 = 𝑥 ∈ ℝ/ 𝑎 < 𝑥 < 𝑏 .
Gráficamente:
 Se llama intervalo cerrado de extremos a y b al conjunto de los x que están entre a y b,
incluyendo los extremos a y b. Escribiremos 𝑎, 𝑏 = 𝑥 ∈ ℝ/ 𝑎 ≤ 𝑥 ≤ 𝑏 .Gráficamente:
 Se llama intervalo abierto a la izquierda al conjunto de los 𝑥 tales que 𝑎 < 𝑥 ≤ 𝑏 .
Escribiremos 𝑎, 𝑏 = 𝑥 ∈ ℝ/ 𝑎 < 𝑥 ≤ 𝑏 . Gráficamente:
( )
a b
[ ]
a b
( ]
a b
8 1 0
3
2

21
 Se llama intervalo abierto a la derecha al conjunto de los 𝑥 tales que 𝑎 ≤ 𝑥 < 𝑏 .
Escribiremos 𝑎, 𝑏 = 𝑥 ∈ ℝ/ 𝑎 ≤ 𝑥 < 𝑏 . Gráficamente:
 Llamaremos intervalos infinitos a los siguientes conjuntos de puntos:
- 𝑥 ∈ ℝ/ 𝑥 > 𝑎 = 𝑎, +∞
- 𝑥 ∈ ℝ/ 𝑥 ≥ 𝑎 = 𝑎, +∞
- 𝑥 ∈ ℝ/ 𝑥 < 𝑎 = +∞, 𝑎
- 𝑥 ∈ ℝ/ 𝑥 ≤ 𝑎 = +∞ 𝑎
- ℝ= −∞, +∞
Observación:
 A + y – no se los debe considerar como números; son solamente símbolos
convencionales que indican todos los números reales hacia la derecha o izquierda de un
número a fijo. Por esta razón, al expresar los intervalos nunca se debe usar corchetes  
junto a los símbolos + y –.
Ejemplos:
1) El conjunto A = {x  ℝ / x  0} es la unión de dos intervalos: A = (–, 0)  (0, +).
2) Consideremos los siguientes conjuntos:
A = {x  ℝ / –2 < x  5} = (–2, 5] y B = {x  ℝ / 0  x} = [0, +)
Gráficamente:
Podemos ver que A  B = {x  ℝ / –2 < x  5 o 0  x} = {x  ℝ / –2 < x} = (–2, +).
También podemos observar que: A  B = {x  ℝ / –2 < x  5 y 0  x} = {x  ℝ / 0  x  5} = [0, 5].
Actividad 17: Considerar los siguientes intervalos: A = (–5, 0] y B = (2, 4). Expresarlos
utilizando desigualdades, representarlos en la recta numérica y hallar:
i) A  B ii) A  B iii) A   iv) B  
]
(
a
[
a
)
a
a
[ )
a b
( ]
[
0
-2 5

22
TRABAJO PRÁCTICO – NÚMEROS REALES
1) Completar con los símbolos , ,  ó  según corresponda.
 4 ........ ℕ
 2 ........ 𝕀
 ℕ ........ ℝ
 {–2,  , 0} ........ ℞
 1
2
........ ℚ
 ℝ ........ ℝ
 0,3 ........ 𝕀
 ℕ ........ ℞ ........ ℚ ........ ℝ
2) Dado el conjunto
5
{12, , 7, 38, 571, , 0.6}
3
S   , encontrar:
a) S  ℕ
b) S  ℚ
c) S  𝕀
d) S  ℞
Representar el conjunto S en la recta numérica en forma aproximada.
3) Decir si las siguientes afirmaciones son verdaderas o falsas:
a) La suma de dos números naturales es siempre un número natural.
b) La diferencia de dos números naturales es siempre un número natural.
c) El cuadrado de un número racional negativo es un racional positivo.
d) Existen infinitos números racionales comprendidos entre 0 y
1
2
.
e) El conjunto de los números naturales carece de primer elemento.
4) Responder:
a) Si m = 14, ¿cómo pueden representarse los números 13, 15 y 16 en términos de m?
b) Sea n un número par cualquiera, ¿cuál es el siguiente entero par? ¿Cuál el anterior?
c) Si x representa cualquier entero impar, ¿cuál es el siguiente entero impar? ¿Cuál el
anterior?
d) Si x es cualquier entero par, ¿x + 1 es un entero par o impar? ¿Y x – 1?
e) Si x es cualquier entero, ¿2x es par o impar? ¿Y 2x – 1? ¿Y 2x + 1?
5) Indicar si las siguientes afirmaciones son verdaderas o falsas. Justificar la respuesta
proponiendo un contraejemplo, en caso de ser falsa, o enunciando las propiedades aplicadas,
en caso de ser verdadera.
a) si a = –2 y b = 0, entonces a : b = 0
b) (–a)  (–b) = –(a . b)
c) el cociente entre un número y su
opuesto es igual a –1
d) a + (–b + c) = a – b + c
e) el inverso de 2 es −
1
2
.
f) a : (b + c) = a : b + a : c,
siendo b + c  0, b  0 y c  0

23
g) b – [–c  (2 – 1) – 1] = b
h) a – (b + c) = a – b + c
i) (b + c) : a = b : a + c, con a  0
j) para todo a  ℝ, a : 1
a = 1
k) para todo a  ℝ , aa  11
)(
l) a  (–b) = a  b
m) a  (b – c) = a  b – a  c
n) la ecuación 2x = 1 tiene solución en ℞
o) –(–a) = a
6) Calcular:
1) (5 + 3)2 = .......... 52 + 32 = ..........
2) 






4
1
3
2
.......... 




 4
4
1
3
2
..........
3) (–2)3 = .......... 3–2 = ..........
4)
2
3
)2( = ..........  23
)2( = ..........
7) Completar con = ó  y mencionar qué propiedades se cumplen o no se cumplen:
a) (a + b)n .......... an + bn
b) ab .......... ba
c)
c
b
a .......... cb
a )(
d) a
qp )(  .......... aa
qp 
8) Resolver aplicando propiedades de la potenciación:
a) 






2
3
2
2
1
b)
  

6
332
6
23
c) 



6
5
13
2
aaaa
d) 







 


5
13
32
12
))(3(2
db
bddb
e) 

4
3
12
5
)5(:2.0
9) En los siguientes cálculos se han cometido errores al aplicar las propiedades. Indicar cuáles
son y corregirlos.
a)     16242532
22222  
b)     155:55:5 0662342
 
c)
 
 
  497
7
77
7
77 2
18
124
29
624




d)   251427 00

10) Aplicar las propiedades de potenciación para demostrar que:
a)       412422 22
 aaa
b)     83:333
32321
  nnn
c)     10002:210
3131
  nn
d)   322222 212
  nnn

24
11) Determinar si han sido resueltos en forma correcta los siguientes ejercicios y justificar:
a) 6329494 
b) 636)9()4(94 
c) 416)8()2( 
d) 743169 
e) 525169 
f) 28
8
64
8:64 3333




12) Indicar si las siguientes afirmaciones son verdaderas o falsas:
a) Si x es un número real, entonces .2
xx 
b) Si x es un número real, entonces .2
xx 
c) Si x es un número real, entonces .3 3
xx 
d) Si x es un número real, entonces .3 3
xx 
13) Unir con flechas las expresiones iguales, siendo 𝑎, 𝑏 𝜖 ℝ+
:
 3 95
21664 ba  ab3

25
400
4
 4 879
cba 3 23
24 aab
 4 224
2
2
81
16
2
1
3
5
5 ba
a
b
aab  4 322
abbca
14) Calcular:
a) 25.0
16 c) 

6
1
3
1
2
22
e) 










2
2
1
2
1
33
b)  25.0
16 d) 









1
3
1
3
2
5
55
f)
 



















2
1
3
1
2
1
5
3
15) Expresar como potencia de exponente fraccionario y calcular:
a)
2
8
13
1
13







 = d) 


4
216 325.0
g) 


27125
35 3
b) 









3 5
2
7
7
1
7
e)  4
273 h) 

3
a
aa

25
c) 

3
a
aa
f)
  

5
4
8
22
16) Demostrar que: 2
1
2
1
2
1
2
1
ba
ba
ba



.
17) Expresar el subconjunto de los números reales que satisface las condiciones siguientes como
un intervalo o unión de intervalos:
x  4 y x < 5
x < 2 y x  –3
x > –5 o x < –6
x  –1
x > –2
x < 2 o x  4
18) a) Determinar el conjunto de los números naturales que satisfacen –3  x < 7.
b) Determinar el conjunto de los números enteros que satisfacen -  x  e.

26
POLINOMIOS
Alguna vez en la escuela media, en clases de Física, hemos visto expresiones tales como
𝑠𝑡 = 𝑣. 𝑡 + 𝑠0 que representa la relación posición (s) de un móvil, que se desplaza en movimiento
rectilíneo uniforme, en función del tiempo (t). O del movimiento uniformemente variado, donde
la expresión utilizada es 2
00
2
1
attvsst  .
En Economía, suele utilizarse expresiones como 𝐶 = 600𝑥2
+ 320𝑥 + 150 que representa, por
ejemplo, el costo total de construir un depósito de materiales.
Es necesario, entonces estudiar las expresiones de la forma:
𝑃 𝑥 = 𝑎0 + 𝑎1 𝑥 + 𝑎2 𝑥2 + ⋯ + 𝑎 𝑛 𝑥 𝑛
(1)
Que llamaremos polinomios, donde los 𝑎0, 𝑎1, 𝑎2,… , 𝑎 𝑛 se llaman coeficientes y son números
reales o complejos (nosotros sólo trabajaremos con reales); x es la indeterminada y los
exponentes de x son todos enteros no negativos.
Actividad 1: Indicar cuáles de estas expresiones son polinomios reales (con coeficientes reales)
a) 2
5
1
x b) 453 32
 xx c) 5. 𝑥−1
+ 𝑥4
d) 3. 𝑠𝑒𝑛(2𝑥) e) 4𝜋𝑥4
+ 2𝜋𝑥2
+ 𝜋 f) 7 −
1
𝑥
g) 10 h) 2 𝑥
− 3 𝑥
+ 4 𝑥
i) 4
43 xxx 
Al conjunto de todos los polinomios en la indeterminada x con coeficientes reales lo
simbolizaremos ℜ 𝑥 .
En la expresión (l) el coeficiente 𝑎0 es el término independiente, y el coeficiente 𝑎 𝑛 es el
coeficiente principal, si 𝑎 𝑛 ≠ 0.
Si 𝒂 𝒏 ≠ 𝟎 , y 𝒂 𝒌 = 𝟎 para todo nk  diremos que n es el grado de P(x) y escribiremos
   nxPgr  .
Si 1na el polinomio se llama mónico.
Por ejemplo, en 425)( 3
 xxxP el grado es 3; xxQ  4)( es de grado 1; xxxxV 463)( 72

es de grado 7 y S(x) = 23 es de grado 0.
El polinomio nulo es aquél donde todos los coeficientes son 0. No está definido el grado del
polinomio nulo.

27
Según el número de términos con coeficientes no nulos, el polinomio se llama monomio,
binomio, trinomio,....
En el ejemplo precedente, S(x) es un monomio, Q(x) es binomio, P(x) y V(x) son trinomios.
Actividad 2: Ejemplificar:
a) binomio de tercer grado b) monomio de quinto grado
c) trinomio de cuarto grado d) monomio de grado cero
Definición:
Dados dos polinomios P y Q decimos que son iguales si y sólo si los coeficientes de los términos
de igual grado son iguales, por ejemplo 𝟑 − 𝒙 𝟑
+ 𝟕𝒙 𝟒
− 𝟒𝒙 𝟓
= 𝟑 + 𝟎𝒙 + 𝟎𝒙 𝟐
− 𝒙 𝟑
+ 𝟕𝒙 𝟒
− 𝟒𝒙 𝟓
.
Al polinomio del segundo miembro se lo llama completo, porque siendo de grado 5, se escriben
todos los términos de grado igual o menor que 5 colocando coeficiente 0 en los términos que
faltan.
Actividad 3: Determinar los valores de m, n, r y s para que T(x) = G(x)
a) 52
2
1
253)( xxxxT  ; 532
)()(
3
4
)2()( xsnxrxrsxmnmxG 
b) 432
8242723)( xxxxxT  ; 4232
)()(3)( xnxsrmxrnmxxG 
Operaciones con Polinomios
Veremos las operaciones con polinomios y las propiedades que éstas verifican.
AAddiicciióónn
La suma del polinomio 𝐴 𝑥 = 𝑎0 + 𝑎1 𝑥 + 𝑎2 𝑥2 + ⋯ + 𝑎 𝑛−1 𝑥 𝑛−1
+ 𝑎 𝑛 𝑥 𝑛
y el polinomio
𝐵 𝑥 = 𝑏0 + 𝑏1 𝑥 + 𝑏2 𝑥2 + ⋯ + 𝑏 𝑛−1 𝑥 𝑛−1
+ 𝑏 𝑛 𝑥 𝑛
+ ⋯ + 𝑏 𝑚 𝑥 𝑚
donde n  m, es el polinomio:
𝐴 𝑥 + 𝐵 𝑥 = 𝑎0 + 𝑏0 + 𝑎1 + 𝑏1 𝑥 + 𝑎2 + 𝑏2 𝑥2
+ ⋯+ 𝑎 𝑛−1 + 𝑏 𝑛−1 𝑥 𝑛−1
+ 𝑎 𝑛 + 𝑏 𝑛 𝑥 𝑛
+ ⋯ + 𝑏 𝑚 𝑥 𝑚
Ejemplo: 5452
473)(;
2
1
253)( xxxxBxxxxA 
A(x) + B(x) = (3 + 3) + (5 1)x + (2 + 0) x2 + (0 + 7)x4 + (1/2  4)x5
A(x) + B(x) = 6  6x + 2x2 + 7x4 9/2 x5
En la práctica puede adoptarse esta disposición en la que se encolumnan los términos de igual
grado (llamados términos semejantes).

28
542
54
52
2
9
7266
473
2
1
253
xxxx
xxx
xxx




Para poder enunciar alguna conclusión sobre el grado del polinomio suma resolver:
  43
221 xxxxA  ;   22 2
 xxxB ;   234
32 xxxxC  ; y   322 34
 xxxxD
A(x) + B(x) = .............................................................................gr (A+B) = .....................
A(x) + C(x) = .............................................................................gr (A+C) = .....................
A(x) + D(x) = .............................................................................gr (A+D) = .....................
El grado del polinomio suma A + B es ………………………… que el grado del polinomio de
mayor grado entre los polinomios sumandos.
 La suma de polinomios goza de las mismas propiedades que la suma de números.
Actividad 4: Dados los polinomios 43
221)( xxxxA  ; 22)( 2
 xxxB ; 3
2
1
)( 2
 xxxF
a) ¿Existe elemento neutro para la suma de polinomios? ¿Cuál es?
b) ¿Todo polinomio tiene un opuesto, o inverso aditivo? ¿Cuál es?
 Recordar que para todo polinomio A(x) existe otro K(x) tal que A(x) + K(x) da por resultado
el polinomio nulo. Se dice que K(x) es el opuesto de A(x) y se lo representa como A(x).
Hallar, entonces, los opuestos de A(x), B(x) y F(x).
SSuussttrraacccciióónn
Dados los polinomios A(x) y B(x), efectuar la sustracción (resta o diferencia) entre A(x) y B(x)
equivale a sumar a A(x) el opuesto de B(x).
Por ejemplo: Si 232)( 345
 xxxxA y 353)( 24
 xxxB . Entonces 353)( 24
 xxxB
Por lo tanto:     )353()232())(()( 24345
 xxxxxxBxAxBxA
    153 2345
 xxxxxBxA

29
Actividad 5:
1) Dados 34
82)( xxxxF  , 43
2)( xxxG  , 122)( 43
 xxxxH , hallar:
a) F(x) + G(x)  H(x)
b) F(x)  G(x)  H(x)
c) F(x)  (G(x)  H(x))
2) Siendo 432
8242723)( xxxxxT  y 23
22442)( xxxxJ  , resolver:
a) T(x) + J(x) b) T(x)  J(x) c) J(x)  T(x)
3) Hallar V(x) tal que W(x)  V(x) = Y(x) , si 3
42
3
1
)( xxxW  y 14
3
2
)( 23
 xxxxY
Producto
Al multiplicar dos monomios, el resultado es otro monomio.
Por ejemplo: si 𝐴 𝑥 = 6𝑥3
y 𝐵 𝑥 = 4𝑥5
, entonces 𝐴 𝑥 ∙ 𝐵 𝑥 = 6𝑥3
∙ 4𝑥5
= 6 ∙ 4 ∙ 𝑥3
∙ 𝑥5
= 24𝑥8
Si 𝐴 𝑥 = 6𝑥3
y 𝐿 𝑥 = −3𝑥4
, entonces 𝐴 𝑥 ∙ 𝐿 𝑥 = 6 ∙ −3 ∙ 𝑥3
∙ 𝑥4
= −18𝑥7
El coeficiente del producto es el producto de los coeficientes de los factores. El grado del
monomio producto es la suma de los grados de los factores, si estos no son nulos. Si alguno de
los factores es el polinomio nulo, el producto es el polinomio nulo.
Para calcular el producto de dos polinomios, multiplicamos cada término (monomio) de uno de
ellos por cada uno de los términos (monomio) del otro.
Si   n
n
n
n xaxaxaxaaxA  

1
1
2
210 ...... y   m
m
m
m xbxbxbxbbxB  

1
1
2
210 ......
Entonces:
        



m
m
m
m
n
n
n
n xbxbxbxbbxaxaxaxaaxBxA 1
1
2
210
1
1
2
210 ............
   
   
   
 m
m
m
m
n
n
m
m
m
m
n
n
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
n
n
n
n
xbxbxbxbbxa
xbxbxbxbbxaxbxbxbxbbxa
xbxbxbxbbxaxbxbxbxbba
xbxbxbxbbxaxaxaxaa




















1
1
2
210
1
1
2
210
1
1
1
1
2
210
2
2
1
1
2
2101
1
1
2
2100
1
1
2
210
1
1
2
210
......
..................
............
............

30
Por ejemplo, si 12)( 3
 xxxA y 43)( 2
 xxxB , entonces resulta:
12()()( 3
 xxxBxA )∙( 43 2
 xx ) =  432 23
 xxx  43 2
 xxx  431 2
 xx =
= 4343826 223345
 xxxxxxxx =
= 454526 2345
 xxxxx
Si queremos utilizar la disposición práctica:
454526
)(.143
)(.43
)(.2826
43
12
2345
2
23
3345
2
3






xxxxx
xBxx
xBxxxx
xBxxxx
xx
xx
Para deducir el grado del polinomio producto resolvemos los siguientes ejemplos.
Actividad 6: Considerar M(x) = x + 3, G(x) = x 2 + 2x  1, B(x) = 2x 3  x + 2 y calcular:
M(x) ∙ G(x) = ...............................................................................gr (M ∙ G) :...................
M(x) ∙ B(x) = ............................................................................. ..gr (M ∙ B) :..................
G(x) ∙ B(x) =.................................................................................gr (G ∙ B) :..................
El grado del polinomio producto es igual a ……………… de los grados de los polinomios factores.
El coeficiente principal del polinomio producto es …………………….. de los coeficientes
principales de los polinomios factores.
El término independiente del polinomio producto es ……………………. de los términos
independientes de los polinomios factores.
La multiplicación de polinomios verifica la ley de cierre (el producto de dos polinomios es otro
polinomio).
Actividad 7:
1) Dados los polinomios T(x) = 2  x + 1/2x 2 , V(x) = x  2, W(x) = x + 1 + x2,
a) Comprobar que T(x) . (V(x) + W(x)) = T(x) V(x) + T(x) W(x)

31
b) Calcular V 2, W 2, V 3.
2) Con los polinomios 324
3752)( xxxxA  , 13)(  xxB , 35
32)( xxxC  calcular:
a) C(x)  A(x) ∙ B(x) b) 3A(x) + 2x3 B(x) c) [B(x)]2  2A(x)
División
Si deseamos determinar los números enteros c y r que satisfacen la ecuación 9 = 4c + r,
podemos efectuar la división entera mediante el correspondiente algoritmo:
donde 9 es el dividendo, 4 el divisor, 2 es el cociente y 1 es el resto. Entonces, c = 2 y r = 1 son
los únicos números enteros que verifican la igualdad 9 = 4 ∙ 2 + 1, teniendo en cuenta que
0 ≤ r < divisor. Además recordamos que el divisor nunca es cero. Esto que sucede en el conjunto
de los números enteros es muy similar a lo que ocurre con los polinomios.
Para hallar los polinomios C(x) y R(x) que satisfacen la ecuación
  )()().2(4423 2334
xRxCxxxxx 
podemos realizar la división de polinomios. El polinomio C(x) se llama polinomio cociente y el
polinomio R(x) se llama polinomio resto. El polinomio divisor nunca puede ser el polinomio
nulo y el grado de R(x) debe ser menor que el grado del divisor o R(x) = 0.
El cociente y el resto de dividir un polinomio por otro no nulo se calculan mediante un
algoritmo similar al de la división de números enteros. Ejemplificaremos cada paso con el
polinomio  4423 34
 xxx dividido por  23
2xx  :
1º: Se ordenan según las potencias decrecientes de la indeterminada (x), el dividendo y el
divisor; completando además el dividendo.
En el ejemplo, ambos polinomios están ordenados, pero hay que completar el dividendo:
44023 234
 xxxx
2º: Dividimos el primer término del dividendo con el primer término del divisor, obteniéndose
así el primer término del cociente.
En el ejemplo:
x
xxxxxx
3
244023 23234

3º: Multiplicamos el primer término del cociente por todo el divisor. En el ejemplo:
xxx
xxxxxx
363
244023
34
23234


9 4
1 2

32
4º: Se resta este producto del dividendo, obteniéndose un nuevo dividendo.
En el ejemplo:
23
34
23234
08
363
244023
xx
xxx
xxxxxx



5º: Reiteramos el procedimiento 2º, 3º y 4º hasta obtener el polinomio resto, de grado menor que
el divisor.
En el ejemplo:
4416
168
08
8363
244023
2
23
23
34
23234





xx
xx
xx
xxx
xxxxxx
Y como   24416 2
 xxgr y   32 23
 xxgr , quedan entonces determinados el polinomio
cociente 83)(  xxC y el polinomio resto R(x) = 16x 2  4x  4 que verifican:
 4423 34
xxx (x 3  2x 2) (3x + 8) + (16x 2  4x  4)
Planteamos otro ejemplo. Queremos efectuar A : B siendo 12)( 3
 xxxA y 1)( 2
 xxxB .
En el ejemplo anterior, restábamos el producto de cada monomio por el divisor. En este ejemplo
procederemos de otra manera, sumando el opuesto del polinomio obtenido en cada paso.
1
222
132
22222
1102
2
2
23
223





x
xx
xx
xxxx
xxxxx
Luego: 12 3
 xx = ( 12
 xx ) (2x + 2) + ( x 1)
Actividad 8:
1) Dados A y B determinar C y R tal que A = B∙ C + R, donde R(x) = 0(x) o gr (R) < gr (B)
a) 12)( 23
 xxxxA 1)(  xxB
b) 123)( 24
 xxxA 22)(  xxB
c) 1)( 23
 xxxxA 1)( 2
 xxB
d) 32)( 2
 xxxA 2
3)( xxB 

33
e) 32)( 2
 xxxA 3
2)( xxB 
f) 4
4)( xxA  2)( 2
 xxxB
2) a) Hallar el polinomio A(x) (dividendo), sabiendo que el divisor es B(x) = 3x  1, el cociente
es C(x) =  x 2 
2
1 x + 1 y el resto es R(x) = 5.
b) Hallar el polinomio divisor B(x) siendo el dividendo 1043)( 23
 xxxxA , el cociente
C(x) = x + 2 y el resto R(x) = 2.
Cuando tenemos que dividir un polinomio P(x) por un polinomio mónico (coeficiente principal
igual a 1) de grado uno, conviene utilizar un algoritmo llamado Regla de Ruffini. Este es un
procedimiento que permite hallar el cociente y el resto sin efectuar la secuencia que describimos
anteriormente. Recordemos que únicamente puede usarse la regla de Ruffini si el divisor es
un polinomio de la forma ax  , siendo a un número real cualquiera.
Ejemplificaremos dicho procedimiento efectuando la división entre A(x) = 3x 3 + 7x 2 + 6x  1 y
B(x) = x + 2
La disposición práctica requiere que en el primer renglón se escriban los coeficientes del
dividendo ordenado y completo hasta el término independiente inclusive. En el ángulo se
escribe el opuesto de a, que figura en el divisor (su raíz).
3 7 6 1
2 6
3 1
3 7 6 1
2 6 2
3 1 4
3 7 6 1
2 6 2 8
3 1 4 9
El resto es 9, siempre es una constante. Los valores 3, 1 y 4 son los coeficientes del polinomio
cociente ordenado y completo, cuyo grado es una unidad menor que el grado del dividendo.
Entonces   413 3
 xxxC .
El coeficiente principal del dividendo (3)
se copia abajo. Se lo multiplica por 2 y
el resultado (6) se escribe debajo del
siguiente coeficiente del dividendo (7). Se
suma 7 y 6 y el resultado (1) se escribe
abajo.
El 4 obtenido en el paso anterior reinicia el
ciclo: se lo multiplica por 2 y el resultado
(8) se escribe debajo del último coeficiente
del dividendo (1). Se suman 1 y 8, y el
resultado (9) es el resto. Se escribe abajo.
El 1 obtenido en el paso anterior reinicia el
ciclo: se lo multiplica por 2 y el resultado
(2) se escribe debajo del siguiente
coeficiente del dividendo (6). Se suman 2 y 6
y el resultado (4) se escribe abajo.

34
Según el algoritmo de la división podemos escribir:
3x 3 + 7x 2 + 6x  1 = (x + 2) (3x 2 + x + 4)  9.
Actividad 9:
1) En la Actividad 8.1), identificar las divisiones en que se puede aplicar la regla de Ruffini,
resolver mediante este método y verificar los resultados anteriores.
2) Obtener mediante la regla de Ruffini el cociente y el resto de la división entre A(x) y B(x).
a) 1426)( 23
 xxxxA B(x) = x + 2
b) 32
334128)( xxxxA  B(x) = x  4
c) 42)( 24
 xxxA B(x) = x + 3
d) 43
)( aaxxA  B(x) = x  ½
3) Para resolver las siguientes divisiones aplicando la regla de Ruffini, hay que recordar que si
se multiplican (dividen) el dividendo y el divisor por un número distinto de cero, el cociente
no varía pero el resto queda multiplicado (dividido) por dicho número.
a) 12)( 3
 xxxA B(x) = x + 2
b) 4826)( 23
 xxxxA B(x) = 2x  1
c) 863)( 2
 xxxA B(x) = 3x  6
Divisibilidad de Polinomios
Si al realizar la división entre A(x) y B(x), con 0)( xB , el resto es el polinomio nulo, decimos
que A(x) es divisible por B(x), o que B(x) divide a A(x).
B(x) divide a A(x) si y sólo si existe un polinomio K(x) tal que K(x)∙ B(x) = A(x).
Por ejemplo, si queremos ver si A(x) = x 2  5x + 6 es divisible por B(x) = x  2, podemos dividir
utilizando la regla de Ruffini:
1 -5 6
2 2 -6
1 -3 0
Como R(x) = 0, entonces A(x) es divisible por B(x).
Para analizar si A(x) = x 5  x 3 + x 2  2x + 1 es divisible por B(x) = x 2 + 1, usamos el algoritmo
conocido ya que, no puede aplicarse la regla de Ruffini.

35
0
1
1
22
22
12
1120
2
2
3
23
335
22345






x
x
xx
xxx
xxxx
xxxxxx
Como R(x)=0, A(x) es divisible por B(x).
Observemos que en el algoritmo, en lugar de restar el polinomio obtenido en cada paso, se sumó
su opuesto, como ya hicimos antes.
Actividad 10: Averiguar si A(x) es divisible por B(x).
a) 10291832)( 367
 xxxxxA B(x) = 2x 2 + 3x
b) 635
162)( xxxxA  B(x) = x2 +2x
c) 151096)( 246
 xxxxA B(x) = 2x 2  3
Veremos otro modo de averiguar la divisibilidad de un polinomio por otro de la forma (x  a)
(siendo a un número real cualquiera).
Para ello debemos definir el valor numérico de un polinomio:
Dado un polinomio P(x) llamamos valor numérico de P(x) para x = a, con a R, al número que
se obtiene reemplazando x por a y efectuando los cálculos.
Ejemplos: En P(x) = x 2  5x + 6,
P(1) = 12  5 . 1 + 6 = 2
P(2) = 22  5 . 2 + 6 = 0
P(1) = (1)2  5 . (1) + 6 = 12
En P(x) = x 4 8,
P(2) = (2) 4  8 = 8
P(0) = 0 4  8 = 8
En P(x) = 5 ,
P(3) = 5 P(-2) = 5 P( 5 ) = 5
Actividad 11: En los polinomios 3
2
1
2)( 2
 xxxA , 1)( 23
 xxxH , 4)( 2
 xxT , calcular:
a) A(1), b) H(2), c) T( 2 ), d) H(0), e) T(-3)

36
Decimos que x = a es raíz de un polinomio P(x) si y solo si P(a) = 0.
Por ejemplo, x = 1 es raíz de P(x) = x 5  x 3 porque P(1) = 1 5  1 3 = 0.
También x = 1 es raíz de P(x), porque P(1) = (1) 5 – (1) 3 = 1 + 1 = 0.
Si realizamos la división de un polinomio P(x) por (x  a) donde a es un número real y R
también es una constante:
P(x) x  a
R C(x)
Entonces
P(x) = (x  a) C(x) + R 
Si x = a, reemplazamos en  y resulta: P(a) =

0
)aa(  C(a) + R  P(a) = R
Enunciamos, entonces, el Teorema del Resto:
El resto de la división de un polinomio P(x) por otro de la forma x  a, es igual a P(a).
Si queremos saber si un polinomio P(x) es divisible por otro de la forma x  a, bastará hallar
P(a). Si P(a) = 0, entonces P(x) es divisible por x  a.
Averigüemos si A(x) = x 2  5x + 6 es divisible por B(x) = x  2, utilizando el teorema del resto:
A(2) = 22 – 5 . 2 + 6 = 0  A(x) es divisible por B(x).
Actividad 12:
1) Analizar si A(x) es divisible por B(x), aplicando teorema del resto.
a) 8)( 3
 xxA B(x) = x + 2
b) 22)( 23
 xxxxA B(x) = x  2
c) 65)( 2
 xxxA B(x) = x  3
2) Halla k para que B(x) sea divisor de A(x)
a) 4)( 23
 kxkxxxA B(x) = x  1
b) kxkxxkxxA  234
)( B(x) = x – ½

37
Factorización de Polinomios
Cuando expresamos un número entero como producto de otros, decimos que estamos
factorizando ese número. Por ejemplo, 120 se puede escribir como 12∙ 10 pero, ¿éstos serán los
únicos factores que puedo encontrar o, podré seguir factorizándolo? La respuesta es sí, veamos
que,
120 = 12 ∙ 10
Pero también, 120 = 6 ∙ 2 ∙ 2 ∙ 5
y, 120 = 3 ∙ 2 ∙ 2 ∙ 2 ∙ 5
es decir, 120 = 3 ∙ 23
∙ 5
En esta última forma de factorizarlo vemos que 120 quedo expresado como producto de
números primos, por lo que ya no podremos encontrar otra factorización que involucre números
positivos más pequeños que los hallados y diremos que esa factorización en números primos es
única, salvo el orden de los factores.
De la misma manera, cuando expresamos un polinomio P(x) como producto de una contante por
otros polinomios diremos que lo estamos factorizando y cada uno de esos nuevos polinomios
será un factor de P(x). Además, las raíces de cada uno de ellos también serán raíces de P(x).
Por ej, analicemos el polinomio 𝑃 𝑥 = 𝑥4
− 𝑥3
− 4𝑥2
− 2𝑥 − 12
Si evaluamos al polinomio en 𝑥 = −2, 𝑃 −2 = 0 lo que significa que 𝑥 = −2 es raíz de P.
Así, podríamos reescribir a 𝑃 𝑥 = 𝑥3
− 3𝑥2
+ 2𝑥 − 6
𝑃1(𝑥)
𝑥 + 2
Pero, ¿P tendrá más raíces reales? Es decir, ¿los factores que intervienen en la factorización de
P tendrán raíces reales?
Sea, 𝑃1 𝑥 = 𝑥2
+ 2
𝑃2(𝑥)
𝑥 − 3
Vemos que 𝑥 = 3 es raíz de 𝑃1, que es uno de los factores de 𝑃 por lo que 𝑥 = 3 también es raíz
de P y vemos también que 𝑃2(𝑥) no tiene raíces reales por lo que
𝑃 𝑥 = 𝑥2
+ 2 𝑥 − 3 𝑥 + 2
estaría así, totalmente factorizado en ℝ 𝑥 .
Si al escribir un polinomio como producto hay más de un factor que tiene la misma raíz, a ésta
se la llama raíz múltiple.
En )5()2()2()(  xxxxQ , x = 2 es una raíz doble de Q. Si M(x) = (x + 3) (x + 3) (x + 3), x = 3
es raíz triple de M(x).
Se llama orden de multiplicidad de la raíz a del polinomio P(x) a la cantidad de veces que
está el factor  ax  en la factorización de P(x).
En )5()1()5()1()1()( 2
 xxxxxxQ , el orden de multiplicidad de la raíz x = 1 es 2.
En M(x) = (x + 2) (x + 2) (x + 2) = (x + 2)3, el orden de multiplicidad de la raíz x = 2 es 3.

38
Un polinomio de grado n tiene como máximo n raíces reales:
 Si el polinomio es de grado impar tiene como mínimo una raíz real.
 Si el polinomio es de grado par, o no tiene raíces reales o tiene una cantidad par de ellas.
Queremos ahora descomponer un polinomio en factores. Vamos a recordar algunas técnicas.
Factor Común
Si en un polinomio, la indeterminada x figura en todos los términos, es conveniente sacar factor
común. También puede extraerse un número que es factor en todos los coeficientes.
Ejemplos: )6(3183)( 2
 xxxxxP
)23(2462)( 22234
 xxxxxxxF
)1()( 223
 xxxxxG
H(x) = 10x 3  25 = 5 (2x 3  5)
Siempre es posible controlar que el producto que obtuvimos es correcto aplicando la propiedad
distributiva.
Diferencia de Cuadrados
Recordemos que una diferencia de cuadrados puede escribirse como producto
x2  a2 = (x + a)∙(x  a).
Cuando se presenta la resta de dos términos y cada uno de ellos es una potencia cuadrada,
puede expresarse como el producto entre la suma y la diferencia de las bases de esas potencias.
Ejemplos: )5()5(25)( 2
 xxxxJ
)6)(6(36)( 224
 xxxxK
)32()32()94()94()94(8116)( 2224
 xxxxxxxL
Muchas veces es posible combinar las diferentes técnicas para factorizar polinomios:
)3()3()9(9)( 22224
 xxxxxxxxD
Actividad 13: Expresar cada E(x) como productos de polinomios del menor grado posible:
a) 23
2)( xxxE  b) 26
)( xxxE  c) xxxE 123)( 3

Factor común por grupos
Algunos polinomios presentan una estructura que permite formar grupos de igual cantidad de
términos y sacar factor común en cada uno de esos grupos. Una vez hecho esto, aparece un
nuevo factor común. Veamos en un ejemplo:

39
  )57(2)57()1014()57(101457 44545
 xxxxxxxxxxV
En los dos términos que se obtienen, 7x  5 es factor común. Entonces el polinomio queda
factorizado:   )2()57( 4
 xxxV
Otros ejemplos:
a)
)1()23()23()23(
)23()23(2323)(
52323235
2357823578


xxxxxxxx
xxxxxxxxxxxW
b)
)1()1()1(1)1(
)1()(1)(
42224
246246


xxxxx
xxxxxxxY
Pero aún podemos descomponer ambas diferencias de cuadrados:
)1()1()1(
)1()1)(1()1()1()1()1()1()1()(
222
222


xxx
xxxxxxxxxxY
Es importante recordar que la potenciación NO es distributiva respecto de la suma ni de la
resta.
(x + 1)2  x2 + 1 (x  1)2  x2  1
Trinomio Cuadrado Perfecto
Recordemos que el resultado de elevar un binomio al cuadrado es un trinomio:
222
2)( aaxxax 
Donde un término es x2; otro es a2 y en otro aparece el doble del producto entre x y a.
A este trinomio se lo llama trinomio cuadrado perfecto, porque proviene del cuadrado de un
binomio.
Analicemos los siguientes ejemplos:
a) C(x) = x 2 + 10x + 25
(x) 2 (5) 2
2 . x. 5 entonces C (x) = (x + 5) 2
b) G(x) = 9x 2 6x + 1
(3x) 2 (1) 2

40
2 . 3x . 1 entonces G(x) = (3x  1) 2 ó G(x) = (3x + 1)2
c) L(x) = 100x4x
25
1 36

2
3
x
5
1





 (10) 2
10.x
5
1
.2 3
 entonces
2
3
10
5
1
)( 





 xxL
Cuatrinomio Cubo Perfecto
Ya hemos visto que 32233
33)( axaaxxax  ()
Entonces al polinomio 8126)( 23
 xxxxM lo comparamos con ()
(x) 3 (2) 3
3.(x) 2.2
3.x.(2)2
Y resulta M(x) = (x + 2) 3
Actividad 14: Factorizar los siguientes polinomios:
a)
4
1
)( 2
 xxxP c) 234
2)( xxxxP 
b) 133)( 369
 xxxxP d) 8126)( 23
 xxxxP
Otros polinomios
Ya hemos repasado algunas técnicas útiles para factorizar polinomios: factor común, factor
común por grupos, diferencia de cuadrados, trinomio cuadrado perfecto y cuatrinomio cubo
perfecto, pero estos métodos son aplicables sólo a polinomios que tienen formas particulares.
¿Cómo hacer cuando los polinomios no son factorizables con estos métodos?, ¿cómo
descomponerlos en factores primos? En general, este no es un problema sencillo de resolver y se
utilizan métodos de aproximación. Sin embargo, en todos los casos se pueden encontrar raíces
de cualquier polinomio mediante prueba con valores de la indeterminada x que se crea pueden
ser raíces.
Recordemos el concepto de valor numérico de un polinomio. Por ejemplo,
Si P(x) = x 3  8 entonces: P(1) = 13  8 = 7; P(2) = 23 8 = 0

41
Si T(x) = x 3 + 1 entonces: T(1) = 13 + 1 = 2; T(1) = (1)3 + 1 = 0
Observamos que algunos valores numéricos son iguales a cero. Entonces decimos que:
2 es raíz de P(x)
1 es raíz de T(x)
a es raíz de P(x) si y sólo si P(x) es divisible por (x  a)
Esta propiedad es aplicable a cualquier polinomio.
Si S(x) = x 4 3x + 2 y S(1) = 14 3 . 1 + 2 = 0 entonces, 1 es raíz de S(x).
Utilizando esta propiedad, podemos descomponer los tres polinomios dados:
Si 2 es raíz de P(x) = x 3  8, entonces x 3  8 es divisible por x  2.
1 0 0 -8
2 2 4 8
1 2 4 0  x 3  8 = (x 2 + 2x + 4) (x  2)
Si 1 es raíz de T(x) = x 3 + 1, entonces x 3 + 1 es divisible por x + 1.
1 0 0 1
−1 -1 1 -1
1 -1 1 0  x 3 + 1 = (x 2  x + 1) (x + 1)
Si 1 es raíz de S(x) = x 4 3x + 2, entonces x 4 3x + 2 es divisible por x  1.
1 0 0 -3 2
1 1 1 1 -2
1 1 1 -2 0  x 4 -3x + 2 = (x 3 + x 2 + x - 2) (x - 1)
Para hallar las raíces racionales de un polinomio, es conveniente conocer el Teorema de
Gauss:

42
Cuando una fracción irreducible
q
p es raíz de un polinomio con coeficientes enteros, p es divisor
del término independiente y q es divisor del coeficiente principal.
Si queremos encontrar las raíces racionales de un polinomio con coeficientes enteros, debemos
seguir estos pasos:
I. Hallar los divisores del término independiente (p) y los divisores del coeficiente principal
(q).
II. Formar con ellos todas las fracciones irreducibles
q
p , que son las posibles raíces.
III. Hallar el valor numérico del polinomio para esas fracciones para ver si alguna es raíz de
él.
Ejemplo: Factorizar al polinomio: 684)( 234
 xxxxxP .
Verificamos que el polinomio tiene coeficientes enteros.
I. Divisores del término independiente, (p): {1, 1, 2, 2, 3, -3, 6, 6}
Divisores del coeficiente principal, (q): {1, 1}
II. Para hallar todas las fracciones irreducibles p/q, notamos que los posibles valores de q
son 1 y 1, por lo tanto p/q será igual a p, para cada caso. Es decir que las posibles raíces
racionales de P(x) son los valores de p, o sea, los divisores del término independiente.
III. Y ahora, con un poco de suerte e intuición para que la tarea sea más breve, se calcula el
valor numérico de P(x) para distintos valores de p, hasta encontrar alguna raíz:
P(1) = 14  4 . 13 + 12 + 8 . 1 – 6 = 0  1 es raíz de P
Entonces, P(x) es divisible por x  1
1 4 1 8 6
1 1 3 2 6
1 3 2 6 0
El polinomio P(x) queda, en principio, factorizado como:   )1(623)( 23
 xxxxxP
Busquemos ahora las raíces de 623)( 23
 xxxxQ .

43
Observamos que las posibles raíces racionales de Q son las mismas que las de P.
Evaluamos Q(1) = 13  3 . 12  2 . 1 + 6 = 2  0 por lo que 1 no es raíz de Q.
Calculamos Q(1) = (1)3  3 . (1)2  2 . (1) + 6 = 4  0
Ahora Q(2) = 23  3 . 22  2 . 2 + 6 = 2  0.
Puede ser Q(2) = (2)3  3 . (2)2  2 . (2) + 6 = 12  0. … Hasta aquí no se tuvo suerte
Seguimos: Q(3) = 33  3 . 32  2 . 3 + 6 = 0. ¡Al fin!!!
Entonces Q(x) es divisible por x  3. También P(x) es divisible por x  3 porque si 3 es raíz de
Q(x) también es raíz de P(x).
1 3 2 6
3 3 0 6
1 0 2 0
El polinomio P(x) queda expresado así: )1()3()2()(
)(
2
 xxxxP
xQ
  
Nos queda hallar las raíces de H(x) = x2 2. Son 22  xyx , que no pertenecen al conjunto
de los racionales, pero pueden encontrarse aplicando la técnica de la diferencia de cuadrados.
Entonces P(x) queda completamente factorizado de la siguiente manera
)1()3()2()2()(  xxxxxP
Donde las raíces reales de P(x) resultan ser .13,2,2  xyxxx
Existen polinomios cuyos coeficientes no son enteros y, sin embargo, también podemos buscar
sus raíces racionales aplicando el Teorema de Gauss.
Por ejemplo, 1
2
1
2
5
)( 23
 xxxxP . Multiplicando P(x) por 2 obtenemos el polinomio
252)( 23
 xxxxF .
Se puede verificar que las raíces racionales de F(x) son las mismas que las de P(x), a pesar de
que los polinomios son diferentes.
Actividad 15: Factorizar los siguientes polinomios, utilizando cualquiera de las técnicas
descriptas, e indicar cuáles son sus raíces:

44
a) 12164)( 234
 xxxxxT b) 105105)( 23
 xxxxQ
c) 1622)( 2
 xxT d) 3612)( 24
 xxxV
e) 567
532)( xxxxW 

45
EXPRESIONES ALGEBRAICAS RACIONALES
Expresiones racionales- Ecuaciones e inecuaciones
El álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son
desconocidas (incógnitas) y se representan por letras.
El lenguaje simbólico dará lugar a expresiones algebraicas mediante las cuales se traducen los
términos de un problema dado.
Si el problema del gran mago te quedó expresado de esta manera, en lenguaje simbólico, es
porque vos también podés convertirte en mago.
1548
3
93)15(

x
Discute con tus compañeros cual es el “truco” utilizado.
Actividad 1: Traducir a lenguaje algebraico los siguientes enunciados:
 La base y la altura de un rectángulo difieren en 10 unidades.
…………………………………………………………………………………………
 La tercera parte de un número menos el otro.
……………………………………………………………………………………………………
 La suma de un número par y uno impar.
……………………………………………………………………………………………………
La astucia del Gran Mago
El Gran Mago me dijo:
-Piensa un número.
-Añádele 15.
-Multiplica por 3 el resultado.
-A lo que salga restale 9.
-Divide en 3.
-Resta 8.
-Dime lo que sale.
Yo le dije:
-154, Gran Mago.
Y el Gran Mago me dijo instantáneamente:
-El número que pensaste fue el 158.
¿Cómo consigue el Gran mago averiguarlo tan
deprisa?

46
 La distancia d que recorre un móvil se calcula como el producto entre el tiempo t que
tarda y la velocidad v.
………………………………………………………………………………………………….
Las expresiones algebraicas provienen de fórmulas físicas, geométricas, de economía, etc. Con
ellas se puede operar para obtener otras relaciones.
Un tipo especial de expresiones algebraicas son las fracciones algebraicas.
Vamos a acercarnos a ellas resolviendo el siguiente problema:
Actividad 2: “Un peatón recorre 14 km en 4 hs. Los primeros 8 km los recorre a una velocidad
de 1 𝑘𝑚 𝑕 más que la que lleva en los siguientes 6 km”.
Si llamamos v a la velocidad con que recorre el primer tramo, será 𝑣 − 1 la velocidad con que
recorre el segundo tramo.
RECORRIDO VELOCIDAD TIEMPO
PRIMER TRAMO 8 km 𝑣
8
𝑣
SEGUNDO TRAMO 6 km 𝑣 − 1
6
𝑣 − 1
El tiempo total invertido es
1
68


vv
.
A estas expresiones:
v
8
y
1
6
v
las llamamos fracciones algebraicas o expresiones
algebraicas racionales.
Generalizando, son todas aquellas de la forma
)(
)(
xB
xA
donde A(x) y B(x) son polinomios
en x, y B(x) distinto del polinomio nulo.
Por ejemplo,
2
7
x
es una expresión algebraica racional porque el numerador A(x) = 7 es un
polinomio y el denominador B(x) = x  2 también es un polinomio.
También es una expresión algebraica racional
xx
xx
7
32
2
3


.
¿Es
3
3 35


x
xx
una expresión algebraica racional?..............................................................................
La expresión x2  9 es también racional porque x2  9 es un polinomio y 1, su denominador,
también lo es.

47
Simplificación de expresiones racionales
Recordemos que, dado el racional
3
2 podemos hallar otros equivalentes con él: ...
21
14
6
4
3
2

donde 0


 ncon
nb
na
b
a .
Análogamente para la expresión racional
)(
)(
xB
xA
pueden hallarse expresiones racionales
equivalentes:
)()(
)()(
)(
)(
xNxB
xNxA
xB
xA


 siendo B(x) y N(x) cualquier polinomio no nulo.
En ℚ muchas veces se nos presenta el problema de encontrar la fracción equivalente más
simple que una dada. Por ejemplo,
12
7
1132
117
132
77
2




También es posible simplificar expresiones algebraicas racionales cuando existen factores
comunes en el numerador y el denominador, de lo contrario la expresión racional es irreducible.
Consideremos
33
1
23
2


xxx
x . Factorizamos su numerador y su denominador:
)1()1(12
 xxx
)1()1()3()1()3()3()3(33 2223
 xxxxxxxxxxx
Entonces
3
1
)1()1()3(
)1()1(
33
1
23
2







xxxx
xx
xxx
x
Las dos expresiones racionales,
33
1
23
2


xxx
x y
3
1
x
son equivalentes.
Veamos otros ejemplos:
1)
2
)2(3
)2()2(
)2()2(3
)2(
)4(3
44
123
2
2
2
3











x
xx
xx
xxx
x
xx
xx
xx
2)
5
1
)5()5(
5
25
5
222
2
4
2







xxx
x
x
x
¿Por qué esta igualdad es válida para cualquier número real?
...................................................................................................................................................
Actividad 3: Simplificar las siguientes expresiones algebraicas racionales:
a)
96
62
2


xx
x b)
1
2


x
xx c)
xxx
xx
4914
49
23
3

 d)
23
6
2
2


xx
xx

48
Operaciones con expresiones algebraicas racionales
Para operar con expresiones racionales, aplicamos las mismas propiedades y técnicas que para
operar con fracciones numéricas.
Adición y Sustracción
Recordamos que para sumar
21
1
14
3
 necesitamos hallar fracciones equivalentes a los sumandos,
de igual denominador:
42
11
732
2133
73
1
72
3
21
1
14
3








Para sumar (o restar) expresiones racionales de distinto denominador, debemos sumar (o
restar) expresiones equivalentes a ellas que tengan el mismo denominador. Para hallarlo,
factorizamos los denominadores y luego multiplicamos los factores comunes y no comunes con
el mayor exponente con el que figura (mínimo común múltiplo).
 Veamos el siguiente ejemplo:



 43363
2
22
xx
x
xx
Factorizamos los denominadores: 








)4()1()1(3
2
)4()1()12(3
2
22
xx
x
xxx
x
xx
Buscamos expresiones equivalentes con igual denominador:







)4()1(3
)1(3
)4()1(3
)4(2
22
xx
xx
xx
x
Operamos en el numerador y sumamos:
)4()1(3
83
)4()1(3
3382
2
2
2
2






xx
xx
xx
xxx
Como el numerador no tiene raíces reales no puede escribirse factorizado.
 Vamos a calcular 





4
42
103
10
22
x
x
xx
x
Factorizamos los denominadores: 






)2()2(
42
)5()2(
10
xx
x
xx
x
Elegimos un denominador común y hallamos las expresiones equivalentes:







)2()5()2(
)5()42(
)2()5()2(
)2()10(
xxx
xx
xxx
xx
Aplicamos propiedades y restamos: 






)2()5()2(
204102
)2()5()2(
20102 22
xxx
xxx
xxx
xxx
)5()2(
)20(
)2()5()2(
)2()20(
)2()5()2(
4022
)2()5()2(
20142208 222












xx
x
xxx
xx
xxx
xx
xxx
xxxx

49
La suma de expresiones algebraicas racionales es asociativa, conmutativa, cumple la ley de
cierre y posee elemento neutro, P(x)= 0. Recordemos además, que restar es sumar el opuesto.
Actividad 4: Calcular:
a) 





 xxx
x
x 3
1
96
1
9
2
22
b) 







22
21
2062
2
25
5
22
xxx
x
x
x c) 




 222
)1(
1
1
2
)1(
1
xxx
Multiplicación
Para multiplicar dos expresiones racionales
)(
)(
)(
)(
xD
xC
y
xB
xA , procedemos así:
nulosnoxDxB
D(x)B(x)
C(x)A(x)
D(x)
C(x)
B(x)
A(x)
)(y)(,



Por ejemplo:
I)
32
36
)1()3(
3)12(
1
3
3
12
2
2










xx
xx
xx
xx
x
x
x
x
II) Calculamos ahora 








)x4x()9x(
)15x5()x4x(
x4x
15x5
9x
x4x
232
2
232
2
Factorizamos cada uno de los polinomios: 



)4()3()3(
)3(5)4(
2
xxxx
xxx
Simplificamos y obtenemos el resultado:
)3(
5



xx
.
La multiplicación de expresiones algebraicas racionales cumple con la ley de cierre, es
asociativa, conmutativa, tiene elemento neutro (1) y es distributiva respecto de la suma y la
resta.
¿Existe inverso multiplicativo para toda expresión
)(
)(
xB
xA
?
...........................................................................................................................
Actividad 5: Resolver
a)
8126
126
2
44
23
2




xxx
x
x
xx b)
12
1
1
1
)1( 22
3





xxxx
x
x
División
Se llama inverso multiplicativo de una expresión algebraica racional
)(
)(
xB
xA
a la expresión
)(
)(
xA
xB
,
con 𝐵 𝑥 𝑦 𝐴(𝑥) no nulos.
Para dividir dos expresiones algebraicas racionales
)(
)(
xB
xA
y
)(
)(
xD
xC operamos igual que en el
conjunto ℚ :
)()(
)()(
)(
)(
)(
)(
)(
)(
:
)(
)(
xCxB
xDxA
xC
xD
xB
xA
xD
xC
xB
xA


 con 𝐵 𝑥 , 𝐶 𝑥 𝑦 𝐷 𝑥 𝑛𝑜 𝑛𝑢𝑙𝑜𝑠.

50
Por ejemplo:
2
2
26
2
2)3(
)2()1(
2
2
:
3
1
xx
xx
xx
xx
x
x
x
x








Actividad 6:
1) Con las expresiones
6
3
)(
9
42
)( 22






xx
x
xTy
x
x
xP calcular:
a)  ( )P x T x b) P(x) : T(x) c) T(x) : P(x)
2) Resolver:
a)
3
16
:
9
4 4
2
2




x
x
x
x b)
1
63
:
1
105
2




x
x
x
x c)
1
43
:
1
1
1
4
4
2
22













x
xx
x
x
x
x
Actividad 7: Efectuar los siguientes ejercicios combinados:
a)
104
9
6
2
4
2 2
22













x
x
xx
x
x
x b)
4
4
:
2
1
2
1
2









 xxx
c)
4
4
:
2
1
2
1
2


 xxx
d) 





 1
1
:)( 3
x
xx

51
TRABAJO PRÁCTICO - EXPRESIONES ALGEBRAICAS
1) Hallar el valor de a para que el resultado sea un polinomio de grado 4:
)72()2()483( 45235354
xaxxaxxxaxx 
2) Efectuar las siguientes operaciones:
a) 











 )23(
3
1
2
1
5
3 226
xxxx
b) 





 )1(
3
4
2
1
)( 24322
xxxxxxx
c)  )1()1()1()1( 222
xxxx
3) Calcular:
a)  23
)32( xx b) 






2
23
4
3
zz
c)  )12(:)6783( 23
xxxx d)  )1(:)24( 3463
xxxxxx
4) Hallar el dividendo P(x) de una división entera sabiendo que el resto es R(x) = 3x 2 + x, el
cociente C(x) = x 3 y el divisor es D(x) = x 4∙ R(x).
5) Hallar el valor de a para que se cumpla la siguiente igualdad:
  )(33)2()(2 245357
xRxxxaxxxx 
Donde R(x) es el resto de dividir x7 - 2x5 por x3 + x.
6) Para cada par de polinomios, indique si P(x) es divisible por Q(x):
a) xxxQxxxxP 3)(952)( 234

b) 32)(952)( 234
 xxxQxxxxP
c) 1)(312)( 2235
 xxQxxxxxP
d) 1)(312)( 235
 xxQxxxxxP
e) 3)(226)( 352
 xxQxxxxxP
7) Al dividir P(x) axxx  242 23
por Q(x) = x  3, se obtuvo 10 como resto. Hallar el
término independiente de P(x).
8) El polinomio 2
2143)( xxxH  es divisible por Ñ(x) = x  a. Hallar los valores de a para
que eso sea posible.
9) Encontrar el valor de h sabiendo que 4 es raíz de hxxxxM  1175)( 56
10) Encontrar el valor de h sabiendo que 1 es raíz de xhxxxxJ 3110)( 347


52
11) Factorizar:
a) 22
)1()2(  xx b) 123
 xxx c) 34
991 xxx 
d) 23
454 xxx 
12) Realizar las siguientes operaciones, simplificando los resultados cuando sea posible:
a)
1
1
1 4
4
2
2





x
x
x
x
b)
2
2
23
)1(
121
3
1






xx
xx
xx
x
c)
1
2
:
6
43
2




x
x
xx
xx
d)
5
7
:
77
3
9
62
2






 x
x
x
x
x
x
x
e)
9
1
)3(
2
3
1
22




 xxx
f)
3
22
22
2
9
12
:
3
)12(
14
12
3
12
x
xx
x
x
x
x
x
x 







 




g) 














1
:
1 x
x
x
x
x
x

53
EECCUUAACCIIOONNEESS EE IINNEECCUUAACCIIOONNEESS
ECUACIONES
Un problema de ingenio frecuente es:
 Pensar un número.
 Sumarle 10.
 Multiplicar por 2 el resultado.
 A lo que se obtiene, restarle 4.
 Dividirlo por 2.
 Restarle 5.
Si la respuesta, es, por ejemplo, 13, el número pensado originalmente es 10.
¿Cómo se sabe?
Para contestar esta pregunta, expresemos en lenguaje simbólico todas las operaciones
realizadas. Llamémosle x al número pensado originalmente (valor desconocido a averiguar).
Entonces: 135
2
42)10(

x
Aplicando las propiedades conocidas de las operaciones entre número reales, obtenemos:
( 10) 2 4 ( 10) 2 4
5 13 5 13 10 2 5 13 3 13
2 2 2
x x
x x
    
             
Por lo tanto, realizar todos los cálculos pedidos equivale a simplemente sumarle 3 al número
original. De esta manera, restándole 3 a 13 es fácil descubrir cuál había sido el número pensado
en principio.
Observemos que para resolver el problema utilizamos una igualdad en la que un valor era
desconocido. Muchos problemas se resuelven de manera similar, lo que originó el estudio de
las…
Ecuaciones:
Son relaciones de igualdad entre cantidades, algunas de ellas desconocidas.
Por ejemplo: y + 2x = 5, x2 + a = b + 8, 2x + 9 = 17.
En particular, cuando el valor desconocido es uno solo, a dicha ecuación la llamamos ecuación
con una incógnita. Algunos ejemplos de ecuaciones con una incógnita son:
3x + 4 = 5x – 8
2x2 + 20 = 24x –20
log x = 3 – log (x + 2)

54
Actividad 1:
 Si x toma los valores 6, –1 o 10, ¿cuáles de las ecuaciones anteriores se cumplen? ¿Cuáles
no se cumplen?
.....................................................................................................................................
 ¿Podría determinar todos los valores de x que satisfacen la ecuación b)? ¿Por qué?
.....................................................................................................................................
Aquellos valores de x que satisfacen una determinada ecuación se los denomina soluciones de
la ecuación. Por ejemplo: 5 es solución de la ecuación –2x + 4 = –x – 1 puesto que -2 . 5 + 4 = -6
= -5 - 1; sin embargo, 2 no es solución de esa ecuación puesto que –2 . 2 + 4 = 0, mientras que
–2 – 1 = –3 y 0  –3.
El conjunto solución de una determinada ecuación puede:
 Tener un solo elemento: por ej. 2x = 6, la única solución de esta ecuación es x = 3. Verificarlo.
 Tener un número finito de elementos: por ej. x3 + 2
1
x2 – 2
1
x = 0 tiene como soluciones
solamente a 2
1
, –1 y 0. Verificarlo.
 No tener elementos: por ej. x2 = –4, ya que vimos anteriormente que todo número real
elevado al cuadrado da como resultado un número no negativo. En este caso decimos que el
conjunto solución es vacío.
 Tener infinitos elementos: 2x – x = x, puesto que todo número real es solución de dicha
ecuación. ¿Por qué?
Actividad 2:
 ¿Se puede encontrar una ecuación que tenga al número 2 como solución?
.....................................................................................................................................
 ¿Se puede encontrar una ecuación que tenga al número 2 como solución, pero que el conjunto
solución posea más de un elemento?
....................................................................................................................................
 ¿Se puede encontrar una ecuación que no tenga ninguna solución en R?
.......................................................................................................................................
 ¿Se puede decir cuál es el conjunto solución de la ecuación x + 2y = 5?
.......................................................................................................................................
Cuando dos ecuaciones tienen el mismo conjunto solución, diremos que dichas ecuaciones son
equivalentes. Por ejemplo, las ecuaciones 4x + 6 = x + 9 y x – 2 = –1 tienen ambas como
conjunto solución al {1}.
En el ejemplo introductorio, lo que hicimos fue encontrar sucesivas ecuaciones equivalentes a la
dada en un principio, es decir, ecuaciones que tengan el mismo conjunto solución, de manera tal

55
que resulten más fáciles de resolver que la primera. Así, la ecuación equivalente que obtuvimos
fue x + 3 = 13, mucho más simple de resolver que la ecuación original 135
2
42)10(

x .
¿Cómo podríamos obtener ecuaciones equivalentes a una dada? Para esto, nos valemos de
algunas propiedades básicas de las igualdades:
Si a, b, c y d son cuatro números reales cualesquiera, entonces valen las propiedades
siguientes:
1) Reflexividad: a = a, es decir, todo número es igual a sí mismo.
2) Simetría: a = b  b = a, es decir, dados dos números a y b, si el primero es igual al
segundo, entonces el segundo también es igual al primero.
3) Transitividad: a = b b = c  a = c, es decir, si un número a es igual a otro b, y éste
último es igual a un tercer número c, entonces el primero es igual al tercero.
4) Uniformidad con la suma: a = b  a + c = b + c, es decir, si se suma el mismo número a
ambos miembros de una igualdad, se obtiene otra igualdad.
5) Uniformidad con el producto: a = b  ac = bc, es decir, si se multiplican ambos
miembros de una igualdad por el mismo número, se obtiene otra igualdad.
Veamos cómo aplicar dichas propiedades en la resolución de algunas ecuaciones sencillas. Por
ejemplo:
3
1
3
1
1
3
1
3
13
)8(9)8(83
983





x
x
x
x
x
Es importante verificar que el valor obtenido satisface la ecuación porque un error en los
cálculos puede conducirnos a una solución incorrecta.
 Observación: ¿Qué sucedería si quisiéramos aplicar la propiedad uniforme de la
multiplicación con un valor x desconocido? Consideremos la ecuación 2x = 6
Multipliquemos ambos miembros por x, resulta 2x2 = 6x
 ¿Cuál es el conjunto solución de la primera ecuación?
.....................................................................................................................................
 ¿Y de la segunda ecuación?
.....................................................................................................................................
 ¿Son ecuaciones equivalentes?
.....................................................................................................................................
(por la uniformidad con la suma)
(por la uniformidad con el
producto)

56
Conclusión:
Si a ambos miembros de una ecuación se los multiplica o divide por un mismo número distinto
de cero, se obtiene una ecuación equivalente a la primera.
Actividad 3: Determinar si los siguientes pares de ecuaciones son equivalentes. Justificar.
a) 3x – 5 = –2x y 3x – 5 + x2 = –2x + x2
b) 3x + 4 = 6 y x + 4 = 3
6
c) x2 = 3x2 – 5x y x = 3x – 5
d) 4 . (–2x + 8) = 6x y –2x + 8 = 2
3
x
e) –2 . (x + 9) = 8 y x + 9 = 8 + 2
Clasificación de ecuaciones polinómicas
Determinar el grado de cada polinomio del primer miembro y completar:
𝑃 𝑥 = 2𝑥 − 1 grado(P(x)) = ..............
Ecuación lineal o de primer grado: 2𝑥 − 1 = 0
𝑄 𝑥 = 𝑥2
− 2𝑥 − 3 grado(Q(x)) = ..............
Ecuación cuadrática o de segundo grado: 𝑥2
− 2𝑥 − 3 = 0
𝑅 𝑥 = 𝑥3
+ 2𝑥2
− 𝑥 − 2 ⇒ grado(R(x)) = ..............
Ecuación cúbica o de tercer grado: 𝑥3
+ 2𝑥2
− 𝑥 − 2 = 0
𝑆 𝑥 = 𝑎 𝑛 𝑥 𝑛
+ … … . . + 𝑎1 x+ 𝑎0 ⇒ grado(S(x)) = ...........
Ecuación de grado n: 𝑎 𝑛 𝑥 𝑛
+ … … . . + 𝑎1 x+ 𝑎0 = 0
Resolución de ecuaciones de primer grado
Con las propiedades vistas anteriormente estamos en condiciones de resolver cualquier tipo de
ecuación de primer grado. Veamos ciertos casos particulares.
 Si la ecuación es 2x – 8 = 2(3 + x)
Procedimiento:
68
226282
2682
)3(282




xxxx
xx
xx
(por propiedad distributiva)
(por propiedad uniforme de la suma)
(operando)
¡ABSURDO!

57
¿Qué significa esto? ¿Habremos cometido algún error durante el desarrollo?
No se cometió ningún error. El absurdo provino de que la ecuación dada no tiene solución en los
números reales, es decir, no existe ningún valor de x que satisfaga la ecuación. El conjunto
solución de dicha ecuación es vacío.
 Si la ecuación es : –10x = 5(2x – 4x)
Procedimiento:
xx
xx
xx
xx
xxx

















10
1
10
10
1
10
1010
)2(510
)42(510
Observemos que la ecuación equivalente que obtuvimos se verifica para cualquier valor de x.
Esto quiere decir que cualquier número real verifica la ecuación inicial, es decir, el conjunto
solución de dicha ecuación es infinito. Verificar esto con algunos ejemplos.
 Si la ecuación es : 3𝑥 − 5 = 8
Procedimiento:
3
13
3
1
13
3
1
3
133
58553
853





x
x
x
x
x
En este caso, existe un único valor de 𝑥: ( 3
13
x ) que verifica la ecuación original. El conjunto
solución es unitario.
Conclusión:
Dada una ecuación de primer grado, ésta puede tener:
 ninguna solución.
 una única solución.
 infinitas soluciones.
(operando)
(por propiedad uniforme del producto)
(por propiedad uniforme de la suma)
(por propiedad uniforme del producto)

58
Resolución de ecuaciones de segundo grado
Como hemos visto, una ecuación de segundo grado es de la forma:
02
 cbxax , donde 𝑎 ≠ 0, 𝑎, 𝑏, 𝑐 ∈ ℝ o cualquier expresión equivalente a ésta.
¿Por qué se aclara que 𝑎 ≠ 0? .......................................................................................................
Ejemplos:
 –x2 + 5x – 8 = 6, es una ec. de seg. grado pues es equivalente a: –x2 + 5x – 14 = 0
 x ∙ (7 – x) = x, es una ec. de seg. grado pues es equivalente a: –x2 + 6x + 0 = 0
 5 = 3x2 – 2, es una ec. de seg. grado pues es equivalente a: 3x2 + 0x – 7 = 0
 (x + 2)2 = 0, es una ec. de seg. grado pues es equivalente a: x2 + 4x + 4 = 0
Veamos un caso particular de resolución de una ecuación de segundo grado.
Si la ecuación es: 2x2 + 6x – 8 = 0
En primer lugar, extraemos 2 como factor común: 2∙(x2 + 3x – 4) = 0
Ahora, tenemos que sumar y restar un número para que en la expresión entre paréntesis se
forme un trinomio cuadrado perfecto. Este número es 4
9
. ¿Cómo lo obtuvimos? ¿Por qué lo
sumamos y restamos?
La expresión resulta: 2.(x2 + 3x + 4
9
– 4
9
– 4) = 0
Factorizando el trinomio y operando:
2.[(x + 2
3
)2 – 4
25
] = 0
Dividiendo ambos miembros por 2 y despejando el binomio al cuadrado, resulta:
2
3 25
2 4
x
 
  
 
Como ambos miembros son positivos, podemos calcular sus raíces cuadradas, y se obtiene:
3 5
2 2
x  
De donde: x = 2
5
– 2
3
= 1, o bien x = – 2
5
– 2
3
= –4
Por lo tanto, la soluciones de la ecuación son {1, –4}. Verificarlo.
A este procedimiento se lo conoce como “completamiento de cuadrados”.

59
Apliquemos, ahora, el completamiento de cuadrados para resolver una ecuación general de
segundo grado:
𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0 , donde 𝑎 ≠ 0
02







a
c
x
a
b
xa (podemos hacerlo pues 𝑎 ≠ 0)
En este caso, debemos sumar y restar 2
2
4a
b
para obtener un trinomio cuadrado perfecto.
0
44 2
2
2
2
2







a
c
a
b
a
b
x
a
b
xa  0
42 2
22
















a
c
a
b
a
b
xa
Dividiendo por 𝑎 ≠ 0 , calculando el denominador común 4𝑎2
y despejando el binomio al
cuadrado, resulta:
2
22
4
4
2 a
acb
a
b
x







 
2
2
4
4
2 a
acb
a
b
x

 

a
acb
a
b
x
2
4
2
2

 
a
acb
a
b
x
2
4
2
2

 

a
acbb
x
2
42


Observemos que, mediante este desarrollo genérico, hemos conseguido obtener una fórmula que
nos permite conocer las soluciones de cualquier ecuación de segundo grado, sin tener que
aplicar el procedimiento de completamiento de cuadrados cada vez que queremos resolver una
ecuación cuadrática. Esta fórmula es la resolvente de la ecuación de segundo grado.
Ejemplo: Si queremos hallar las soluciones de la ecuación –2x2 – 3x = –2, en primer lugar
debemos llevarla a la forma general ax2 + bx + c = 0, donde a  0, es decir, –2x2 – 3x + 2 = 0.
En este caso particular, tenemos que a = –2, b = –3 y c = 2. Luego, utilizando la fórmula ya
vista las soluciones están dadas por:
)2(2
2)2(4)3()3( 2
2,1


x .
Operando se tiene:
4
53
2,1


x , es decir 2
4
53
1 


x y
2
1
4
53
2 


x .
Veamos qué información nos puede brindar sobre las soluciones la fórmula para resolver
ecuaciones de segundo grado:

60
1) Supongamos que tenemos una ecuación de segundo grado en la que acb 42
 = 0.
¿Cómo influye esto en el conjunto solución?
.....................................................................................................................................
2) Supongamos que ac4b2
 < 0. ¿Qué sucede en este caso? ¿Cómo son las soluciones?
.....................................................................................................................................
3) ¿Qué sucede, en cambio, cuando acb 42
 > 0? ¿Cómo son las soluciones?
.....................................................................................................................................
 Observación: Notemos que al obtener las soluciones de una ecuación polinómica de la
forma 02
 cbxax lo que se hace es hallar las raíces del polinomio cbxaxxP  2
)( .
Conocidas las raíces 1r y 2r , esto nos permite escribir al polinomio en la forma
))(()( 21 rxrxaxP  , es decir, escribirlo totalmente factorizado.
Recíprocamente, si tenemos un polinomio escrito de la forma ))(()( 21 rxrxaxP  , es
decir, factorizado, sabemos que 1r y 2r son las soluciones de la ecuación 0))(( 21  rxrxa .
Conclusión:
Dada una ecuación de segundo grado, ésta puede tener:
 ninguna solución real.
 una única solución real doble.
 dos soluciones reales distintas.
Ejemplo: Sea el polinomio P(x) = 4x2 + 8x – 12. Para hallar las raíces, planteamos la ecuación
4x2 + 8x – 12 = 0 y encontramos sus soluciones mediante la fórmula resolvente de la ecuación de
segundo grado: 1r = 1, 2r = –3.
Luego, el polinomio factorizado resulta: P(x) = )3x)(1x(4  .
Actividad 4: Resolver las siguientes ecuaciones:
1) x2 – 5x = 2x2 + 6x + 2 – x2
2) 2x2 = –18
3) x.(x – 1)(x + 2) = x3
4) – 3
2
x2 + 2 x – 2
1
= 0
5) (x + 3)2 = 12x
6) x2 + 3x = 3.(x2 + x) – 2x2
Resolver los siguientes problemas:
1) Julieta empleó la mitad de su dinero en comprar ropa y la mitad del resto en paseos.
Si aún le quedan $10, ¿cuánto dinero tenía?

61
2) La edad de Pablo elevada al cuadrado es igual a cinco veces la edad que tendrá
dentro de 10 años. ¿Qué edad tiene Pablo?
Ecuaciones fraccionarias que se resuelven mediante ecuaciones de primer y segundo
grado
Llamamos ecuaciones fraccionarias a aquellas de la forma 0
)x(Q
)x(P
 , donde 𝑃 𝑥 y 𝑄(𝑥) son
polinomios, 𝑄(𝑥) ≠ 0, o a aquellas ecuaciones que se pueden llevar a esta forma.
Por ejemplo, son ecuaciones fraccionarias:
 3
2
1



x
x pues es equivalente a 0
2
72
0
2
631
03
2
1









x
x
x
xx
x
x .
 0
2
51

xx
pues es equivalente a 0
2
7
0
2
52


xx
.
 0
2
43
2
3



x
xx
Intentemos resolver la siguiente ecuación fraccionaria: 0
1
12



x
x . Para esto, aplicamos las
propiedades ya conocidas.
Multipliquemos ambos miembros por x +1:
)1x(0)1x(
1x
1x2


  01x2
  1x1  y 1x2  .
Verificar si 1x y 2x son solución de la ecuación original. ¿Qué sucede? ¿Qué error hemos
cometido?
...........................................................................................................................................
Conclusión:
Cuando resolvemos una ecuación del tipo 0
)(
)(

xQ
xP , debemos descartar como posibles
soluciones a los valores de x que anulan el denominador Q(x), es decir, los valores que
satisfacen la ecuación Q(x) = 0. Esto se debe a que no está definida la división por 0.
Actividad 5: Resolver y verificar las soluciones encontradas:
a) 2
2
1


x
x
b) 1
32
3

x
x
c) 0
2
4
2
3



 xx
d)
x
x
x
x





6
6
3
3

62
ECUACIONES LINEALES CON DOS INCÓGNITAS
Analicemos ahora las ecuaciones lineales con dos incógnitas. Por ejemplo: 2𝑥 − 𝑦 = 3. Para
encontrar una solución de dicha ecuación, debemos hallar un par de números que la satisfaga.
A diferencia de lo que ocurre con las ecuaciones lineales con una incógnita, en las ecuaciones
lineales con dos incógnitas siempre se encuentran infinitas soluciones. Notemos que si
despejamos la incógnita 𝑦 en la ecuación dada, obtenemos 𝑦 = 2𝑥 − 3. Entonces para cada valor
de 𝑥 encontramos un valor de 𝑦. Este par de números (𝑥, 𝑦) es una de las infinitas soluciones de
la ecuación dada.
Por ejemplo, los siguientes pares de números son solución de la ecuación 2𝑥 − 𝑦 = 3:
0, −3 ; 1, −1 ;
5
2
, 2 .
En efecto, si reemplazamos estos valores en la ecuación inicial 2𝑥 − 𝑦 = 3, veremos que se
satisface la igualdad:
2.0 − −3 = 3 ; 2.1 − −1 = 3 ; 2
5
2
− 2 = 3
A continuación expresamos el conjunto formado por todas las soluciones de la ecuación dada,
llamado el conjunto solución o solución general:
𝑆𝑔 = 𝑥 , 2𝑥 − 3 , 𝑥 ∈ ℝ
Otra forma de hallar los pares que son solución de la ecuación dada es despejando la variable
𝑥, obteniendo el conjunto solución
𝑆𝑔 =
𝑦
2
+
3
2
, 𝑦 , 𝑦 ∈ ℝ
Observemos que ambos conjuntos solución son equivalentes, aunque estén expresados de
distinta manera.
INECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA
Algunos problemas nos conducen a plantear desigualdades. Resolvamos la siguiente situación.
El tanque de nafta de un auto puede contener hasta 45 litros. Tiene conectado un sistema
automático de alarma que se enciende cuando sólo quedan 8 litros en él. ¿Cuántos litros de
nafta es posible cargar cuando recién se enciende la señal?
Si con x designamos la cantidad de litros que podemos cargar, el problema queda planteado con
la siguiente desigualdad:
8 + x  45
Donde 8 representa la reserva, x los litros a cargar y 45 la capacidad máxima del tanque.
La desigualdad planteada es una inecuación.
Definición: Una inecuación es una desigualdad que contiene incógnitas (valores desconocidos).

63
De la misma forma que para resolver ecuaciones necesitamos conocer las propiedades de las
igualdades, ahora necesitaremos conocer las propiedades de las desigualdades para poder
resolver inecuaciones.
Propiedades de las desigualdades
 Consideremos la desigualdad –2 < 7 y sumemos a ambos miembros el número 8. ¿Cómo
es dicha desigualdad respecto de la original?
..............................................................................................................................
 Consideremos la misma desigualdad, –2 < 7, pero sumemos a ambos miembros el
número negativo –8. ¿Cómo es dicha desigualdad respecto de la original?
...................................................................................................................................
Conclusión:
Si sumamos a ambos miembros de una desigualdad un número real cualquiera, la
desigualdad se mantiene en el mismo sentido. En símbolos: Sean a, b, c  R,
si a < b, entonces a + c < b + c.
 Ahora, consideremos la desigualdad 5 < 10 y multipliquemos ambos miembros por 4. ¿Cómo
es dicha desigualdad respecto de la considerada?
.............................................................................................................................
 Partamos de la misma desigualdad, 5 < 10, y multipliquemos ambos miembros por el
número negativo –4. ¿Cómo es dicha desigualdad respecto de la considerada?
..............................................................................................................................
Conclusión:
a. Si multiplicamos ambos miembros de una desigualdad por un número
positivo, la desigualdad resultante mantiene el sentido de la primera. En
símbolos: Sean a, b, c  R, si a < b y c > 0, entonces a.c < b.c
b. Si multiplicamos ambos miembros de una desigualdad por un número
negativo, la desigualdad resultante cambia su sentido respecto de la primera.
En símbolos: Sean a, b, c  R, a < b y c < 0, entonces a.c > b.c
Ahora estamos en condiciones de resolver el problema planteado en un principio. Debíamos
resolver la inecuación: 8 + x  45.

64
Resolución:
37
)8(45)8(8
miembros)ambosa8(sumando458



x
x
x
Luego, podemos cargar cualquier cantidad de litros, siempre que sea menor o igual que 37.
Veamos otro ejemplo: resolver la inecuación 4
3
42

 x
.
Resolución:
4
2
1
8
2
1
2
)
2
1
(82
)4(12)4(42
1242
343
3
42
34
3
42





















x
x
mbiagualdad cay la desibros por -ambos miemmosmultiplicax
x
x
x
mantiene)gualdad sey la desipormiembrosamos ambos(multiplic
x

 Dar dos valores de x que verifiquen la inecuación original y dos valores que no la
verifiquen.
..............................................................................................................................
 ¿Cuántos son los valores de x que verifican la inecuación del ejemplo? Graficarlos en la
recta numérica.
..............................................................................................................................
 Observación: El conjunto solución puede ser expresado utilizando la notación de
intervalos. En el ejemplo, el conjunto solución es el intervalo [–4, +).
Actividad 6:
 Consideremos la siguiente inecuación: 30)5x(38x3  . ¿Cuál es su conjunto
solución?
..............................................................................................................................
 Dada la inecuación: x
x


3
2
52
. ¿Cuál es su conjunto solución?
..............................................................................................................................

65
Hay situaciones en las que los valores requeridos deben satisfacer dos condiciones a la vez o
simplemente alguna de ellas. Veamos cómo proceder en cada uno de estos casos.
Encontrar los valores reales de x que satisfacen:
1) 22
2
1
x y 102  x (ambas condiciones deben satisfacerse a la vez)
La solución de la primera inecuación está dada por {x  ℝ: x < 8} = (–, 8).
Por otra parte, para la segunda ecuación, el conjunto solución es: {x  ℝ : x  –5} = [–5, +).
La solución del ejercicio está dada por los x que satisfacen ambas inecuaciones a la vez, es decir,
los valores de x que pertenecen a ambos conjuntos solución.
En símbolos: {x  ℝ : x < 8 y x  –5} = (–, 8) ∩ [–5, +) = [–5, 8).
Gráficamente:
2) x
x


2
3
2
o 21x
(los valores de x deben satisfacer al menos una de las inecuaciones)
La solución de la primera inecuación está dada por {x  ℝ : x  –2} = (–, –2].
Por otra parte, para la segunda ecuación, el conjunto solución es: {x  ℝ : x  3} = [3, +).
La solución del ejercicio está dada por los x que satisfacen al menos una de las inecuaciones, es
decir, los valores de x que pertenecen a un conjunto solución o al otro.
En símbolos: {x  ℝ : x  –2 o x  3} = (–, –2] U [3, +).
Gráficamente:
Actividad 7: Resolver las siguientes inecuaciones y expresar su conjunto solución mediante
intervalos, graficándolos en la recta numérica.
a) 51
4
3
x b)    22323  aa
c) Las edades de Hernán, Darío y Guido suman más de 52 años. Hernán es un año menor
que Guido y tres años mayor que Darío. ¿Qué edad tiene como mínimo Hernán?
d) 285 z y 5z  e) 1
3
2
2
3



 xx
f)
3
21
2
1 xx 


o 5
3
1
)2(
2
1
 xx
[ )
-5 8
] [
3-2

66
Trabajo Práctico – Ecuaciones e Inecuaciones
1) a) La solución de la ecuación 4x – 8 = 2x – (–x) – (–1) es:
 un número fraccionario y entero.
 un número entero y negativo.
 9
 7
9
 ...ninguna de éstas.
b) La solución de la ecuación: 5x + 10x –6 – 9 + 4x = x + 3 – 12 es:
 15
 3
2
 2
3








3
2
 ninguna de éstas.
c) El valor de m que pertenece a ℕ y que es solución de la ecuación
m + 3(4m – 6) = –10 + 2(3m –5) es:
 0
 inexistente








7
2
 2
 ninguna de éstas.
2) Resolver las siguientes ecuaciones de primer grado y determinar la cantidad de elementos
del conjunto solución:
a) )15(
2
1
4 xx  b) (y – 1)(2 + y) = 5 – y(4 – y) – 2y
c)
6
185
)9(3
x
x

 d)
3
2
5
6
1
3
4
2
2
5








 aa
a
a
e) a – x = 3(x – a), siendo x la incógnita y a un número real fijo.
f) 5t + 4 – t = 4(1 + t) g) y – 2 = 6(x + 4), siendo ambas, x e y, incógnitas.
3) Hallar las soluciones de las siguientes ecuaciones e identificar cuáles de ellas son
equivalentes:

67
a) 𝑦 −
1
4
2
=
9
16
d) 3x2 + 3(3x – 1) = 2(3x + 2x2) – 13
b)
5
6
𝑥 + 3
2
= 5𝑥 + 8 e) 𝑤2
−
1
2
𝑤 −
1
2
= 0)
c) −3 𝑥 − 1 𝑥 +
1
2
= 0 f) −
1
2
𝑥2
= −
3
2
𝑥 − 5
4) Factorizar los siguientes polinomios:
a) P(x) = x2 – 25 c) R(x) = 3x2 – 12x – 63
b) Q(x) = –2x2 + x – 10 d) S(x) = 3x2 – 12x + 12
5) Responder:
a) ¿Es posible encontrar valores de x que satisfagan (x + 3)(x – 3) = 5(x + 2) + 31 y
0
4
153

x
al mismo tiempo?
b) ¿Es posible encontrar valores de t que satisfagan 8t2 = –4t y t
t
3
4
3
22 2


a la vez?
6) Decir si las siguientes afirmaciones son verdaderas o falsas. Justificar.
a) El conjunto solución de la ecuación 15
2 2


x
xx
está dado por {0, –7}.
b) El par (x, y) = (5, 2) es solución de la ecuación 3x2 – 2y = 51 + 10y.
c) Las ecuaciones 0
3
)3( 2



a
a
y 03a  son equivalentes.
d) 1 es raíz doble del polinomio P(x) = x2 + x – 2.
7) Resolver los siguientes problemas:
a) De un depósito lleno de líquido se saca la mitad del contenido; después, la tercera parte del
resto y quedan aún 1.600 litros. Calcula la capacidad del depósito.
b) Hallar dos números naturales impares consecutivos tales que su producto sea 255.
c) Un poste de luz de 7 m. se rompe y al doblarse, la punta de la sección rota toca el suelo a 3
m. de la base del poste. ¿A qué altura se rompió? (Ayuda: utilizar el Teorema de Pitágoras).
d) Pienso un número, le sumo 5, a este resultado lo multiplico por 3 y el nuevo resultado lo
divido por 10. Obtengo así 6. ¿Qué número pensé?
e) El perímetro del siguiente triángulo es 24 cm. ¿Cuál es la longitud de cada uno de sus
lados?
15x2

x1
x3

68
f) Un rectángulo tiene por dimensiones el triple y el quíntuplo del lado de un cuadrado.
Calcula las dimensiones de ambos cuadriláteros, sabiendo que la diferencia entre sus áreas
es de 2015 cm2.
8) Resolver y representar gráficamente la solución de las siguientes inecuaciones:
a) 5x < –5 b) 2x + 3  7 c) 82
3
42


x
x
d) 48
2
1
x y
3
7
3
5

 x
e)   523 x o   812  x
f) xxx 31035  y  3335 22
 xxx
9) Resolver los siguientes problemas:
a) Recuerda que cada lado de un triángulo es menor que la suma de los otros dos y mayor que
su diferencia. Imagina que x e y son dos lados de un triángulo cuyo valores son x = 1 e y =
12. ¿Qué podrías decir del lado z?
b) Un padre, para estimular a su hijo a que estudie matemática, promete darle $3 por cada
ejercicio bien resuelto, pero, por cada uno que esté mal, el hijo le dará $2. Ya van por el
ejercicio 26 y el muchacho recibe de su padre $38. ¿Cuántos ejercicios ha resuelto bien y
cuántos mal?
c) Un matrimonio dispone de $130 para asistir a un espectáculo con sus hijos. ¿Cuántos
pueden ser éstos si ese dinero no alcanza para tomar localidades de $25 cada una y, en
cambio, sobra para tomar localidades de $20 cada una?
d) Por ahora yo tengo el doble de tu edad. Pero cuando tú tengas mi edad, la suma de los
cuadrados de nuestras edades será 26 veces la suma de las mismas. ¿Cuál es la edad de cada
uno?

69
FUNCIONES
Problema 1: Observar el siguiente gráfico, extraído del diario La Nación del 6 de marzo de
2001, que representa la producción y la venta de automóviles en nuestro país durante un año.
¿En qué mes fue la máxima producción de autos?
a. ¿En qué período cayeron más las ventas?
b. ¿En qué meses hubo mayor diferencia entre la producción y la venta de automóviles?
Problema 2: Leer el prospecto de un remedio antitérmico para niños (FIGURA 1)
a. ¿Qué cantidad de remedio le daría a un bebé que pesa 5 kg y tiene 37,7º de temperatura?
b. ¿Cuánto pesa Nico si debe tomar 12 ml cada 6 horas y tiene 38,2º de temperatura?
Problema 3: Los teléfonos actuales tienen asignados a sus teclas letras y números, por lo que a
muchas empresas que contratan el servicio de 0800 le asignan números fáciles de memorizar
para sus clientes. Así, por ejemplo, una escuela podría tener el 0800372852, que se corresponde
con el 0800ESCUELA.
a. ¿Qué número habrá que marcar para comunicarse con el 0800HELADOS?
b. ¿A qué palabra corresponderá el 08001843367?
Es usual encontrar información presentada en forma de gráficos. Ellos nos muestran
relaciones entre distintas variables, como por ejemplo: la recaudación impositiva
durante los meses de un año, la esperanza de vida en cada país, el crecimiento de una
población de bacterias en un determinado período, entre otras.
Muchas de estas relaciones son funciones; en algunos casos, es posible describirlas a
través de fórmulas matemáticas, los cuales permiten predecir comportamientos.

70
Problema 1: Para responder a las preguntas de este problema, debemos analizar el gráfico. En
él se representan los meses del año en el eje horizontal y las unidades productivas o vendidas,
en el vertical. Si bien no está indicada la escala en el eje vertical, se incluye dentro del gráfico
algunos puntos que nos permiten deducir que cada división en ese eje representa 500 unidades
y que comienza desde el 10000.
Cuando nos proponemos averiguar en qué mes fue la máxima producción de autos, tenemos que
buscar el punto en que la producción alcanzó su mayor valor.
Esto sucedió en marzo de 2000.
Observemos en el gráfico correspondiente a las ventas que entre octubre y noviembre de 2000
fue el período en el que más cayeron las ventas.
Para la tercera pregunta, analizamos ambos gráficos simultáneamente. La mayor distancia
entre las curvas se observa en noviembre de 2000; por lo tanto, es en ese mes cuando se produjo
la mayor diferencia.
Problema 2: Si el bebé tiene menos de 38º, tenemos que seguir la primera indicación: debemos
darle 0,3 ml ∙ 5 = 1,5ml cada 6 horas. Nico, que tiene más de 38º y hay que darle 12ml cada 6
horas, pesa 24 Kg, pues 0,5 ∙ 24 = 12.
Problema 3: Cuando estudiamos la relación planteada en este problema, vemos que es sencillo
contestar a la primera pregunta porque a cada letra le corresponde un número; por lo tanto,
para la heladería marcamos 08004352367. En cambio, no sucede lo mismo en el caso de la
pregunta b. pues a cada número le corresponde más de una letra y, por lo tanto, no hay una
única combinación de letras que se vincule a este número telefónico. Por ejemplo, TIDENS y
UGFENS, entre otros.
Función
En todos los problemas anteriores se vinculan, en distintas situaciones, varias variables: el
gráfico del primer problema relaciona la producción por un lado, y por otro, las ventas en el
mismo período; en el prospecto se vincula la cantidad de remedio al peso del chico y su
temperatura axilar.
En cada uno de estos problemas consideramos dos variables, por ejemplo, la cantidad de autos
vendidos y cada mes del año. En este caso decimos que la cantidad de autos es la “variable
dependiente” del mes considerado, que es la “variable independiente”.
Vemos que en los dos primeros problemas podemos responder a las preguntas porque a cada
valor de la variable independiente le corresponde un único valor de la variable dependiente.
En cambio, en el último ésto sucede sólo con la relación que le asigna a cada letra el número
que está en la misma tecla por haber varias posibilidades. Además, al 1 y al 0 no se les asigna
ninguna letra. Nos interesa analizar ahora aquellas relaciones que vinculan todos y cada uno
de los valores de la variable independiente a un único valor de la dependiente.

71
Por ejemplo:
  xxxg 65
 Es función porque si a cada número real lo elevamos a la quinta y le restamos
seis veces ese mismo número, obtenemos siempre un número real.
Problema 4: Roberto tiene 2 m de varilla de madera para armar un marco rectangular.
Consideren las posibles medidas del marco y completen la siguiente tabla que vincula el ancho
al largo del mismo:
Largo del marco (metros) 0,4 1
Ancho del marco (metros) 0,5 1,5
El marco de Roberto puede medir, por ejemplo:
Roberto tiene muchas posibilidades para construir su marco, pero no puede fabricar uno de 1 m
de largo ni de 1,5 m de ancho, porque en estos casos no tendría suficiente varilla para los cuatro
lados.
Las medidas del marco de Roberto deben ser más pequeñas que 1. Por lo tanto, los valores que
puede medir el largo son los números reales entre 0 y 1.
Dominio e imagen de una función
Por ejemplo, el dominio de la función del problema 4 es el conjunto de los números reales entre
0 y 1.
Una relación entre dos variables es función si a cada valor de la variable
independiente le corresponde un único valor de la variable dependiente.
0,5 cm
0,5 cm
0,4 cm
0,6 cm
El dominio de una función f es el conjunto de todos los valores que puede tomar
la variable independiente.
Se denota Dom f o Df.

72
Si analizamos ahora los valores que puede tomar la variable dependiente en el problema
anterior, observemos que tiene las mismas limitaciones que la independiente. Por lo tanto, los
valores que puede pomar la variable dependiente son los números reales entre 0 y 1.
Por ejemplo, la imagen de la función que vincula el precio de venta de un artículo a su precio de
costo es el conjunto de los números positivos con dos cifras decimales.
Analicemos el dominio de algunas funciones numéricas definidas por fórmulas:
   73  xxf
Todas las operaciones que se deben efectuar para hallar la imagen de un valor a través de esta
función son válidas para todo número real, por lo tanto, Dom f = ℝ
Analicemos su imagen: tomemos un número real y cualquiera.
¿Está en la imagen? Para responder a esta pregunta, debemos analizar si existe algún número
x tal que:
 
3
7
73


y
xxyxfy
Este x existe siempre para todo y porque las operaciones son válidas para cualquier número
real. Por lo tanto, la imagen de esta función es el conjunto de todos los números reales. Im f = ℝ
  
x
xg
1

Como la división por 0 no está definida, el dominio de esta función es el conjunto de todos los
números reales distintos de 0, simbólicamente: Dom g = ℝ − 0 .
Si llamamos y al valor que le corresponde a x a través de esta función, para hallar el conjunto
imagen tenemos que analizar qué valores toma y. Para ello escribimos:
y
x
x
y
11

La imagen de una función f es el conjunto de todos los valores que toma la variable
dependiente.
Se denota Im f o If
El conjunto de llegada es un conjunto en el cual está incluida la imagen.
La ley de formación puede estar dada en el lenguaje natural a través de una tabla,
una fórmula o un gráfico cartesiano.
Para definir una función deben darse el dominio, el conjunto de llegada y una ley de
formación

73
Este número x existe para cualquier y distinto de cero. Por lo tanto, la imagen de esta función
es: Im g = ℝ − 0 .
Tal como lo hicimos en este ejemplo, es muy usual llamar y al valor que le corresponde a x a
través de una función. Por este motivo, cuando se define una función a través de su fórmula se
usa indistintamente  f x o y .
Problema 5: La doctora Diet, nutricionista, registra una vez al mes, en un gráfico cartesiano,
la variación del peso en gramos de sus pacientes en función del tiempo.
Este gráfico corresponde a la señora Pacient, quien comenzó la dieta con 98 kg y realiza su
consulta a la doctora Diet una vez por mes.
a. ¿Cuánto pesaba en la tercera consulta?
b. ¿Cuánto aumentó entre el cuarto y el quinto mes?
c. ¿En qué mes esta paciente alcanzó su menor peso? ¿Y el Mayor?
d. ¿En qué períodos bajó de peso?
e. ¿En qué período subió de peso?
f. ¿Hubo algún momento en el que su peso no varió?
g. ¿En qué meses la paciente volvió a pesar lo mismo que al comenzar el tratamiento?
Para responder a las preguntas anteriores debemos tener en cuenta que el gráfico representa la
variación del peso de la paciente, es decir que el punto (3; -2000) nos indica que en el tercer mes
bajó 2000 g.
En la tercera consulta pesaba 96 kg pues había bajado 2 kg. Entre el cuarto y el quinto mes
aumentó un kilo. Si observamos globalmente la gráfica, vemos que desde que comenzó la dieta
y hasta el segundo mes, fue bajando de peso; a partir de allí subió de peso hasta la octava

74
consulta, luego bajó hasta la vista siguiente y volvió a aumentar durante el décimo mes para
luego seguir bajando durante el resto del período registrado.
También podemos ver que en la sexta, novena y undécima consultas pesaba lo mismo que en el
momento que comenzó su tratamiento ya que la variación que muestra el grafico es 0.
Ceros o raíces de una función
Por ejemplo, en el caso de la función que estamos estudiando, los ceros corresponden a los
meses en que la señora Pacient volvió a su peso inicial, es decir que la variación fue nula en
esos meses, lo que ocurrió al sexto, noveno y undécimo meses.
¿Cómo hallamos los ceros en una función dada por su fórmula?
Analicemos la función 𝑓: ℝ → ℝ /   42
 xxf . Estamos buscando los valores de x para los
cuales y vale 0; por lo tanto, simbólicamente escribimos: 2x y 2x
Los ceros o raíces de una función son aquellos valores del dominio cuya imagen es cero.
Recordemos…
Los intervalos son conjuntos de números reales
definidos de la siguiente manera, según sean
cerrados
   bxayxxba  /;
Semiabiertos
   bxayxxba  /;
   bxayxxba  /;
   bxyxxb  /;
   axyxxa  /;
Abiertos
   bxayxxba  /;
   bxyxxa  /;
   bxyxxb  /;
¿Cómo se lee…?
 : para todo
 : existe
 : pertenece
 : entonces
/ : tal que
 : unión

75
Intervalos de crecimiento y decrecimiento
Por ejemplo, si analizamos la función que relaciona la variación del peso de la señora Pacient
con el tiempo, los intervalos de crecimiento son: (2; 3), (4; 8) y (9; 10), y los intervalos de
decrecimiento son (0; 2), (8; 9) y (11; 18).
Máximos y mínimos
Por ejemplo:
(2; 5) es el conjunto de todos los números reales entre 2 y 5, si lo representamos en la
recta numérica:
Un intervalo de crecimiento de una función es un subconjunto I del
dominio para el cual a mayores valores de la variable independiente le
corresponden mayores valores de la variable dependiente. Simbólicamente
escribimos:
   afxfaxsiIaIx  :,
Un intervalo de decrecimiento de una función es un subconjunto I del dominio
para el cual a mayores valores de la variable independiente le corresponden
menores valores de la variable dependiente. Simbólicamente escribimos:
   afxfaxsiIaIx  :,
La función f alcanza un máximo absoluto en el punto a del dominio si para todo x
perteneciente al mismo, x  a, la imagen de x es menor que la de a. simbólicamente
escribimos:
   afxfaxDfx  :,
La función f alcanza un mínimo absoluto en el punto a del dominio si para todo x
perteneciente al mismo, x  a, la imagen de x es mayor que la de a. simbólicamente
escribimos:
   afxfaxDfx  :,
0 2 5

76
Por ejemplo, en el caso de la variación del peso de la señora Pacient, el máximo absoluto se
produce el octavo mes y es de 750 g y, en 18, la función alcanza un mínimo absoluto que es de
-3500 g.
Conjunto de positividad y negatividad
Por ejemplo, en el caso de la señora Pacient, el conjunto de positividad es C+ = (6; 9)  (9; 11).
Por ejemplo, en la función que estamos estudiando, los intervalos para los cuales las imágenes
son negativas son (0; 6), y (11; 18), es decir que C- = (0; 6)  (11; 18).
Funciones pares y funciones impares
El conjunto de positividad (C+) de una función es el subconjunto del dominio
cuyas imágenes son número positivos.
El conjunto de negatividad (C-) de una función es el subconjunto del dominio
cuyas imágenes son número negativos.
Una función f es par si para todo valor de x pertenece al dominio se verifica que:
   xfxf  .

77
Por ejemplo, la función 𝑓: ℝ → ℝ 𝑓 𝑥 = 𝑥2
− 9 es par porque para todo x real se cumple:
     xfxxf  9
2
Por ejemplo, la función 𝑓: ℝ → ℝ   3
5/ xxf  es impar porque para todo x real se
cumple:
       xfxxxf 
33
55
Problema 6: El electrocardiograma es un estudio que registra, durante un tiempo, la actividad
eléctrica del corazón.
Analizar la curva y describir las particularidades que se observan.
Si observamos el gráfico, vemos que una parte de él se repite con regularidad. Cada veinte
cuadraditos, aproximadamente, se vuelve a repetir la misma curva. Decimos que ésta es una
función periódica. En esta caso el período es de poco menos que veinte cuadraditos.
Funciones Periódicas
Por ejemplo, la función f representada a continuación es periódica porque    xfxf 8 , para
todo x perteneciente a su dominio. O sea, se repite cada ocho unidades.
Una función f es impar si para todo valor de x pertenece al dominio se verifica que:
   xfxf  .
Una función f es periódica si existe un número p tal que    xfpxf  , donde p es
el período

78
Problema 7: Una aerolínea registró la altura a la que vuela un avión que parte de un
aeropuerto ubicado a nivel del mar, durante un viaje. Se representó de la siguiente manera:
a. Si el avión parte de un aeropuerto que está a 1000 m de altura respecto del nivel del
mar y realiza un viaje en las mismas condiciones que el anterior, ¿cómo será el grafico
de la función que vincula su altura respecto del nivel del mar al tiempo?
b. ¿Cómo será el gráfico de otro avión que sale desde el nivel del mar y realiza un viaje en
las mismas condiciones pero veinte minutos más tarde que el primero?
Desarrollo:
a. Como las variaciones de la altura son iguales, la altura inicial será 1000 m mayo y lo
mismo sucederá con todas las alturas que alcance el avión durante su vuelo. Por lo
tanto, el gráfico tiene la misma forma pero está corrido 1000 m hacia arriba.
b. En este caso lo que se modifica es la hora de partida, por esto alcanzará exactamente las
mismas alturas que el primer avión pero 20 minutos después. En el gráfico quedará la
misma curva pero corrida 20 minutos hacia la derecha.
Representemos en un mismo par de ejes los tres gráficos para verlo mejor:

79
Corrimientos
Hemos representado la función a(t) que vincula la altura, a, del avión al tiempo expresado en
horas de día, t.
Cuando el avión sale a 1000 m sobre el nivel del mar, a cada valor de la variable dependiente le
sumamos los 1000 m iniciales, es decir, estamos representando
  1000ta
En cambio, en el caso del avión que sale 20 minutos más tarde, se modifica la variable
independiente.
Si llamamos (t) a la función que vincula la altura del tercer avión al tiempo de viaje del mismo,
¿qué relación hay entre el tiempo de viaje desde que parte este avión y el tiempo del primero?
Veamos en una tabla:
T = t – 20
Como las alturas son las mismas:    20 taTb
Analicemos otro tipo de corrimientos.
Problema 8: Un corredor está recorriendo una pista circular. El siguiente gráfico representa la
distancia hasta la largada en función del tiempo.
T 0 20
t 20 40

80
a. ¿Cómo será el gráfico de otro corredor que está recorriendo la misma pista pero lo hace
en la mitad del tiempo?
b. Comparen este último gráfico con el anterior.
El nuevo gráfico se repite en la mitad del tiempo que el anterior, es decir que la gráfica se
“redujo a la mitad”.
Llamemos f(t) a la función que vincula la distancia a la largada del primer corredor al tiempo y,
análogamente, g(t) a la función correspondiente al segundo corredor.
Como vemos en el gráfico, g(t) y f(t) toman los mismos valores en 𝑥 = 0, 3, 6, 9 𝑦 12 , es decir en
los ceros de las funciones.
Ceros de f: 0, 6, 12, 18… Ceros de g: 0, 3, 6, 9…
Vemos que el primer corredor tarda en dar una vuelta el doble de tiempo que el segundo. Por lo
tanto: g(t) = (2t)
Conclusiones
 El gráfico de f(x-a) es el gráfico de f(x) corrido a unidades hacia la derecha
sobre el eje x.
 El gráfico de f(x) +a es el gráfico de f(x) corrido a unidades hacia arriba del
eje y.
 El gráfico de f(ax) es el gráfico de f(x) “reducido ” o “ampliado” a veces según
sea a mayor o menor que 1, respectivamente.
     ,f x a f x a y f ax  se denominan corrimientos de  f x

81
TRABAJO PRÁCTICO - FUNCIONES
1) La siguiente tabla muestra la relación entre dos variables. ¿Esta relación es una función?
En caso afirmativo indicar dominio e imagen.
2) Indicar el dominio de cada una de las siguientes funciones:
a. Precio de un paquete de galletitas en función del peso.
b. Cantidad de harina necesaria para una receta en función de las porciones que se quiere
hacer.
c. Variación de la temperatura en una ciudad en función del tiempo.
3) a. ¿Cuáles de los siguientes gráficos corresponden a funciones 𝑓: ℝ → ℝ? Justificar sus
respuestas.
b. Indicar el dominio y la imagen de las funciones anteriores.
4) Vincular cada función a su dominio:
 
5x
x
xf
  25 xxg
  xxxh 32

 
4
2
2



x
x
xi
 ;25
 ;5
ℝ − −5
ℝ
ℝ+
    ;44;0
ℝ  2;2 
x 3 4 5 6 7 8
y 5 5 5 5 5 5

82
5) Completar los siguientes gráficos de acuerdo con la información que se da de cada uno:
a. h es periódica con período = 4
b. g es impar
6) Considerar las funciones del ejercicio 5. Graficar g(x+3); 4.f(x); h(2x). Indicar si siguen
cumpliendo las condiciones que tenían las funciones originales.
7) En la región de la precordillera hay un arbusto que sirve de alimento a la fauna local. Un
grupo de científicos que teme por su extinción decidió realizar un relevamiento de datos
cuyos resultados fueron volcados en una gráfica.
Observar la gráfica y responder las siguientes preguntas:
c. f es par

83
a) ¿Qué variables se tuvieron en cuenta para realizar la gráfica? (identificar variable
independiente y variable dependiente)
b) Definir en forma coloquial una función g que se corresponda con la gráfica.
c) ¿Cuántos ejemplares por m2 hay a 400 m de altura sobre el nivel del mar?
d) ¿A qué altura sobre el nivel del mar hay 2 ejemplares por m2?
e) ¿Cuál es el mayor número de ejemplares del arbusto, que hallaron por m2?
f) ¿Qué ocurre con el arbusto a partir de los 350 m sobre el nivel del mar?
g) ¿Cuál es la máxima altura sobre el nivel del mar en la que fueron realizadas las
mediciones?
h) ¿Cuál es el dominio de la función g? ¿Cuál es la imagen de g?
8) En el siguiente gráfico aparece el peso de dos hermanos, Nicolás y Lucía, a lo largo de los
años. El peso de Nicolás está representado por la línea azul y el de Lucía por la línea rosa.
a) ¿Cuál era el peso de Nicolás a los 8 años? ¿Y el de Lucía a los 13?
b) ¿A qué edad pesaba Lucía 55 kg? ¿Y Nicolás 70 kg?
c) ¿Cuándo pesaba Nicolás más que Lucía y cuándo pesaba menos?

84
d) ¿Cuándo pesan lo mismo?
e) ¿Cuál fue el aumento de peso de Lucía entre los 3 y los 12 años?
f) ¿Cuál fue el aumento de peso de Nicolás en el mismo período?
g) ¿Cuál fue el aumento de peso de cada hermano entre los 12 y los 16 años?
h) ¿Quién disminuyó de peso, y en qué período?
9) Para evaluar la temperatura en cada tiempo t (en hs) de una cámara en donde se guardaron
semillas de maíz se realizaron registros de la temperatura (en °C) de la misma, en forma
continua, desde las 6 de la tarde de un día y durante las primeras 6 hs del día siguiente.
Para resolver esta situación se puede considerar el gráfico de la función:
Para los registros de temperatura observamos cuatro situaciones bien deferentes en la
evolución de la temperatura a medida que transcurre el tiempo:
 hasta dos horas antes de la medianoche, es decir 26  t , la temperatura fue
aumentando.
 Luego, y hasta la medianoche, 02  t , la temperatura fue disminuyendo.
 Entre la medianoche y la hora 1, es decir 10  t , la temperatura volvió a aumentar,
hasta llegar a los 1°C
a) ¿Cuál fue la máxima temperatura alcanzada?;
b) ¿Cuál fue la mínima temperatura alcanzada?;
c) Expresar cuáles son los intervalos de crecimiento de la función graficada y cuáles de
decrecimiento.
d) ¿En qué intervalo la temperatura permanece constante?
10)Un club dispone de $50.000 mensuales para el sueldo de sus deportistas. La política del club
es que la plata disponible se divide en partes iguales entre los deportistas que asistieron
regularmente todo el mes.

85
a) Completar la siguiente tabla (teniendo en cuenta que todos los deportistas cobran lo
mismo).
Cantidad de Deportistas 20 40 80 100 125
Sueldo de cada deportista
b) Realizar un gráfico para representar la tabla anterior. ¿Tiene sentido unir los puntos por
medio de una línea continua? Justificar la respuesta dada.
c) Hallar una fórmula que le permita al tesorero del club calcular lo que cobra cada
deportista en función de la cantidad de deportistas que asistieron al club.
d) Teniendo en cuenta que el cupo máximo de deportistas es de 125. Hallar el dominio y la
imagen de la función encontrada
e) Si de lo que cobra, cada deportista debe pagar $20 de impuestos, ¿cuál es el número
razonable de deportistas que debe tener el club para que cada uno cobre como mínimo $300?

86
TRIGONOMETRÍA
La palabra trigonometría proviene del griego: trigonos (triángulo) y metria (medida). En sus
orígenes esta rama de la matemática se utilizó para resolver problemas de agrimensura y
astronomía, pero con el desarrollo de la ciencia se ha convertido en un instrumento
indispensable en la física, la ingeniería, la medicina y todo otro proceso en el que se encuentren
comportamientos que se repiten cíclicamente. Sirve para estudiar fenómenos vibratorios, como
por ejemplo la luz, el sonido, la electricidad., etc.
Sistemas de Medición de Ángulos
Para medir ángulos pueden adoptarse distintas unidades. Los sistemas más usados son:
 Sistema sexagesimal, cuya unidad de medida angular es el grado sexagesimal, que es la
noventa-ava parte del ángulo recto y se simboliza 1º. La sesenta-ava parte de un grado es un
minuto (1’) y la sesenta-ava parte de un minuto es un segundo (1”).
"1
60
'1
'1
60
º1
1
90
rectoángulo
 
Un ángulo llano mide 180º y un giro completo mide 360º.
 Sistema circular o radial, cuya unidad de medida es el radián. La proporcionalidad que
existe entre la longitud s de los arcos de dos circunferencias concéntricas cualesquiera
determinados por un ángulo central α y los radios r correspondientes, permite tomar como
medida del ángulo el cociente
r
s
radio
arco
 . Un ángulo central de 1 radián es aquel que
determina un arco que tiene una longitud igual al radio.
Ejemplo: Si β determina un arco de 6 cm en una circunferencia de 2 cm de radio, entonces la
medida en radianes de β es: 3
2
6

cm
cm
r
s
. En el sistema circular, β mide 3 radianes, o decimos
que mide 3, sin indicar la unidad de medida.
La medida en radianes de un ángulo de un giro es 

2
..2

r
r
.
s = r, por lo tanto 1
r
s
 .
Un radián es la medida del ángulo con
vértice en el centro de la circunferencia y
cuyos lados determinan sobre ella un
arco s de longitud igual al radio r.


87
La medida en radianes de un ángulo llano, que es la mitad de un giro, es 


2
..2
La medida en radianes de un ángulo recto es
2

.
Para relacionar un sistema de medición con otro, observemos la siguiente tabla:
Ángulo
Sistema
sexagesimal
Sistema
circular
1 giro 360º 2 
llano 180º 
recto 90º /2
¿A cuántos grados sexagesimales equivale un radián?
Haciendo uso de las proporciones y teniendo en cuenta la medida del ángulo llano, tenemos
π 180º
1 "45'17º57
º1801



Nota:  es aproximadamente igual a 3,14. Un ángulo de  radianes equivale a un ángulo de
180º. Pero   180.
Actividad 1:
a) Expresar en radianes las medidas de los ángulos, si es posible, utilizando fracciones de :
30º 45º 60º 120º
b) Expresar en grados sexagesimales los siguientes ángulos medidos en radianes:
2 1/2 /2 2
c) Efectuar las siguientes operaciones.
 Hallar el ángulo complementario de 56º41’27’’
 Hallar el ángulo suplementario de 102º25’
 ¿Cuánto mide el ángulo que supera en 12º33’ a la quinta parte de 39º40’ ?
 El minutero de un reloj es de 12 cm de largo. ¿Qué recorrido realiza la punta de la
manecilla en 20 minutos?
Razones trigonométricas de un ángulo agudo
Recordemos las definiciones de las razones trigonométricas.
hipotenusa
opuestocateto
sen 
hipotenusa
adyacentecateto
cos 
C

B
A

88
adyacentecateto
opuestocateto
tg 
Observación:
 Estas razones dependen sólo del ángulo  y no de las medidas de los lados del triángulo
construido.
Las definiciones de las razones trigonométricas de ángulos agudos pueden extenderse para
cualquier ángulo. Para eso, consideramos el ángulo  en el plano cartesiano, haciendo coincidir
su vértice con el origen de un sistema cartesiano ortogonal, y su lado inicial con el semieje
positivo de las x.
También definimos las razones trigonométricas recíprocas de las anteriores, llamadas
cosecante, secante y cotangente:
0
0
00 opuestocateto
adyacentecateto
cot
adyacentecateto
hipotenusa
sec
opuestocateto
hipotenua
cosec
y
x
g
x
r
y
r

Observación:
 Las fórmulas anteriores son válidas cuando no se anulen los denominadores.
También se verifican las siguientes relaciones









tg
1
gcot
cos
1
sec
sen
1
eccos
cos
sen
tg
r
x
OP
Pdeabscisa
hipotenusa
adyacentecateto 0
cos 
00
0
0
 xsi
x
y
adyacentecateto
opuestocateto
tg 
r
y
OP
Pdeordenada 0
hipotenusa
opuestocateto
sen 
y0 P
r

x0
x0
P y0
r


89
Ejemplo: Queremos determinar los valores de las relaciones trigonométricas de un ángulo 
cuyo lado terminal pasa por el punto P = (3 , 4)
1
.
..
.
..
.)(
.)(
.)(
.).(
.)(
.).(
22
2
2
2
2
2
2













hip
adycat
hip
opcat
hip
hip
hip
adycat
hip
opcat
Resulta, entonces: (sen )2 + (cos )2 = 1 donde por comodidad escribimos sen 2  + cos 2  = 1
y que llamamos identidad pitagórica.
Esta identidad, por ejemplo, nos permite calcular las funciones trigonométricas de un ángulo α
sabiendo que es agudo y que
5
3
sen  .
Entonces, si sen2  + cos2  = 1  cos2  = 1  sen2    2
s e n1c o s
y como  < /2
5
4
25
16
5
3
1coscoscos
2







3
41
cot
4
5
cos
1
sec
3
51
cos
4
3
5
4
5
3
cos











tg
g
sen
ec
sen
tg
y
Para un ángulo cualquiera, puede aplicarse el
teorema de Pitágoras:
(cat. op.)2 + (cat. ady.)2 = (hipotenusa)2
Dividimos ambos miembros por (hipotenusa)2:
x0 = 3, y0 = 4
4
3
gcot
3
5
sec
4
5
eccos
3
4
tg
5
3
cos
5
4
sen
54)3(r 22









4
P
r

-3
x
y0 P
x0


90
Actividad 2: Sabiendo que cos  =
3
2
, hallar las restantes relaciones trigonométricas de .
Con frecuencia se utilizan expresiones que vinculan a cada una de las relaciones
trigonométricas con las demás para poder utilizar, en cada caso, la expresión más conveniente.
Por ejemplo, podríamos expresar la tangente de  en función del coseno:






cos
cos1
:
cos
2

 tgpitagóricaidentidadlautilizandoy
sen
tg .
Análogamente, podemos expresar el coseno de  en función de la tangente de :
1
cos
1
cos
cos1
coscos 2
2
2
2
2
2
2
2













 tgtg
sen
tg
sen
tg





 22
2
2
2
1
1
cos
1
1
cos
cos
1
1
tgtg
tg




Más adelante veremos cómo seleccionar el signo del resultado.
Actividad 3:
a) Expresar la secante de  en función de la cosecante de .
b) Expresar la tangente de  como función del seno de .
La circunferencia trigonométrica – Ángulos orientados
Cuando trabajamos en radianes, las medidas de los ángulos son números reales. Si definimos
ángulos orientados esta medida puede tomar valores negativos. Al trabajar con un ángulo en un
sistema de coordenadas cartesianas, éste está generado por la rotación de una semirrecta o rayo
que parte del semieje positivo de las x.
Si el lado gira en sentido contrario a las agujas del reloj, se dice que el ángulo es positivo. Es
negativo cuando está generado en sentido horario.
Puede, además, realizar más de un giro completo.
Para referirnos a su ubicación, consideramos el plano cartesiano divido en cuatro sectores,
llamados cuadrantes y una circunferencia con centro en el origen y radio 1 que llamaremos
circunferencia trigonométrica.
I cuadranteII cuadrante
P1
III cuadrante IV cuadrante
P0
P2
P3



δ
P1
En la figura, como r = 1 tenemos
que:
0
00
y
1
y
r
y
sen   el segmento
de ordenadas está relacionado con el
sen 
0
00
x
1
x
r
x
cos   el segmento
de abscisas está relacionado con el
cos 

91
Para hallar el segmento asociado al sen , se construye en el segundo cuadrante el triángulo
rectángulo con las componentes de P1 y el segmento de ordenadas corresponde a seno de .
Análogamente sucede con los ángulos del tercer y cuarto cuadrante, donde el segmento de
ordenada se asocia con el seno del ángulo y el segmento de abscisa, con el coseno del ángulo.
Los signos de los valores de las relaciones trigonométricas de los distintos cuadrantes dependen
de los signos de las coordenadas del punto sobre el lado terminal del ángulo.
Esta información se resume en la siguiente tabla, que podrá completar:
Actividad 4:
a)
sen  cos  tg  cosec  sec  cotg 
I + + +
II 
III 
IV 
b) Si  5
2
9
 , ¿qué se puede asegurar respecto del signo de sen , cos  y tg ?
Razones trigonométricas de ángulos notables
Para los ángulos de 0, /2,  y 3/2, teniendo en cuenta las coordenadas del punto P asociado a
cada ángulo en la circunferencia trigonométrica, podemos deducir y completar:
Actividad 5:
Para los ángulos de /6, /4 y /3 radianes pueden calcularse las razones trigonométricas
usando recursos geométricos. Damos aquí una tabla que contiene los valores de los ángulos
notables pertenecientes al primer cuadrante.
 0 /2  3/2
P (0; 1)
sen  1
cos  0
tg  no existe
-1
-1
1
1
0

92
 0
6

4

3

2

sen  0
2
1
2
2
2
3 1
cos  1
2
3
2
2
2
1
0
tg  0
3
3 1 3
no está
definida
Actividad 6:
1. Construir, observar la circunferencia trigonométrica y completar en los casos en que
existan:






 

sec0cos)5()4cos(
2
ectgsen
2. Calcular, usando la tabla de ángulo notables:
a) 






6
5
sen b) 






4
5
cos c) 






3
2
tg d) 






6
7
cos ec
Algunas Identidades Trigonométricas
Las siguientes identidades son de utilidad para distintos procedimientos, como cálculos de
límites e integrales. No es necesario memorizarlas porque suelen estar incluidas en tablas de
derivadas , integrales, etc. Simplemente enumeramos sólo algunas de ellas.
Para  y  cualesquiera:
sen (   ) = sen  cos   cos  sen 
cos ( +  ) = cos  cos   sen  sen 
cos (   ) = cos  cos  + sen  sen 



tgtg
tgtg
tg



1
)(
Para cualquier :
 sen (2) = 2 sen  cos 
 cos (2) = cos2  sen2

93




2
1
2
)2(
tg
tg
tg



2
cos1
2
 






sen

2
cos1
2
cos
 









cos12 





 sen
tg

2
)2(cos1
cos2 




2
)2(cos12 


sen
Actividad 7: Verificar las siguientes identidades (se aconseja trabajar en cada miembro de la
igualdad sustituyendo las expresiones por otras identidades conocidas hasta llegar a una
igualdad evidente).
Ejemplo:









cos
cos
1
cos
1
cos
1
1sec
:ónDemostraci
cos
cos
1sec




sensen
sensen
sen
sen
a)



sen
tg


1
cos
sec b)


 2
2
2
cos
cot
1
ec
g
sen 
Resolución de Triángulos rectángulos
Resolver trigonométricamente un triángulo rectángulo consiste en, dados algunos elementos del
triángulo, obtener los restantes.
Ejemplo: Resolver el triángulo rectángulo dados la hipotenusa a = 20 cm y 𝐵 = '35º28
a
b
cA B
C
Entonces los datos son: a y Bˆ y las incógnitas Cˆ , b y c.
Como C y B son complementarios, resulta:
𝐶= 90º − 𝐵 = 61º 25’

94
Como sen B = cmcmBsenab
a
b
568,94784,0·20ˆ 
Además, cos cmcmBac
a
c
B 562,178781,0·20ˆcosˆ 
Actividad 8:
a) Para un triángulo rectángulo similar al del ejemplo, hallar c, B y C sabiendo que a = 15 cm. y
b = 9 cm.
b) Un globo sujetado por un cable de 180 m. es inclinado por el viento formando el cable un
ángulo de 60º con la horizontal. Calcular la distancia del globo al suelo.
c) Calcular la longitud que debe tener una escalera para que apoyada en una pared alcance
una altura de 2,85 m al formar con el plano de la base un ángulo de 58º 1’. Rta: 3,36 m.
d) Un alambre carril recto de 320 m. une dos estaciones A y B y tiene una pendiente de 0,532.
Calcular la diferencia de altura sobre el nivel del mar entre A y B. Rta: 150,23
m.

95
BIBLIOGRAFIA
Altman, Silvia - Comparatore, Claudia - Kurzrok, Liliana. “Matemática2: Funciones 1”. Ed.
Longseller, 2005.
Altman, Silvia - Comparatore, Claudia - Kurzrok, Liliana. “Matemática 2: Funciones 2”. Ed.
Longseller, 2005.
Bocco, Mónica. “Funciones elementales para construir modelos matemáticos”. Ministerio de
Educación de la nación. Instituto Nacional de Educación Tecnológica, 2010.
Carnelli, Gustavo – Novembre, Andrea – Vilariño, Alejandra. “Función de gala”. Ed. El
Hacedor, 1999.
Colera, José- Gaztelu, Ignacio - de Guzmán, Miguel - Oliveira, María José. “Matemáticas 2”,
Ed. Anaya, 1997.
Colera, José - García, Juan Emilio - Gaztelu, Ignacio- de Guzmán, Miguel- Oliveira, María José.
“Matemáticas 3”. Ed. Anaya, 1995.
Colera, José- García, Juan Emilio - Gaztelu, Ignacio- de Guzmán, Miguel - Oliveira, María José.
“Matemáticas 4”. Ed. Anaya, 1995
De Guzmán, Miguel - Colera, José - Adela Salvador. “Bachillerato 2”. Ed. Anaya, 1987.
De Guzmán, Miguel - Colera, José - Adela Salvador. “Bachillerato 3”. Ed. Anaya, 1988.
Itzcovich, Horacio – Novembre, Andrea. “M1 matemática”. Ed. Tinta Fresca, 2006.
Itzcovich, Horacio – Novembre, Andrea. “M2 matemática”. Ed. Tinta Fresca, 2006.

Cuadernillo matemática ingreso2013

Más contenido relacionado

La actualidad más candente

Similar a Cuadernillo matemática ingreso2013

Más de Felix Cuya

Cuadernillo matemática ingreso2013