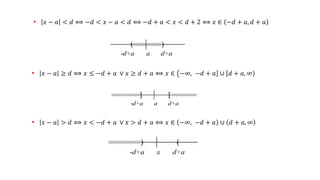
El documento explica el concepto de valor absoluto como la distancia de un número real al cero. Define formalmente el valor absoluto de un número "a" como la misma "a" si es positivo o cero, y como su opuesto "-a" si es negativo. Presenta propiedades clave como que el valor absoluto siempre es positivo o cero, y cómo usarlas para resolver ecuaciones e inecuaciones con valor absoluto.

1. Matemática General
VALOR ABSOLUTO de un número real
Sabemos que cualquier número real tiene su representación en la recta numérica, por lo tanto
es válida la pregunta:
¿Cuál es la distancia de un número real al cero?
Por ejemplo: ¿Cuál es la distancia del 6 al 0?
Es 6
¿Cuál es la distancia del - 6 al cero?
También es 6
Si observamos esto en la recta real tenemos:

2. ➢Una manera de expresar la distancia de un número al cero que
usamos en matemática es por medio del “valor absoluto”.
“El valor absoluto de un número es la distancia de dicho número a cero”
y esta distancia se simboliza poniendo el número entre dos barras
verticales, es decir:
𝒂 simboliza la distancia del número 𝒂 al cero.
Por ejemplo: | 6| = 6 , |−6| = 6 , | -18| = 18 , |3,7| = 3,7 , | 0| = 0 .
Hay algo particular cuando calculamos el valor absoluto de un número y
tiene que ver con lo que ocurre según el signo que tiene ese número, es
decir:
“Si un número es positivo o cero, su valor absoluto coincide con dicho
número, y si un número es negativo, su valor absoluto es el opuesto de
ese número”

3. Entonces:
𝑎 = ቊ
𝑎 𝑠𝑖 𝑎 ≥ 0
−𝑎 𝑠𝑖 𝑎 < 0
Observación: La misma definición de valor absoluto nos asegura que el valor
absoluto de un número siempre será mayor o igual que cero, nunca será negativo.
El valor absoluto de un número real “a” es el mismo número “a” cuando es positivo
o cero, y es el opuesto de a, es decir “- a”, si a es negativo. (En éste último caso, “- a”
se convierte en un número positivo).
Esto se expresa en forma simbólica de la siguiente manera:

4. Veamos si quedó clara la idea de lo que significa el valor absoluto de un
número:
➢ ¿Cuáles son los números reales cuyo valor absoluto es 100?
➢¿Cuáles son los números reales cuyo valor absoluto es -1?
➢Si 𝑐 = 2 entonces 𝑐 = _____ ¿porqué?
➢Si 𝑐 = −7 entonces 𝑐 = _____ ¿porqué?
➢Si 𝑏 > 0 entonces ¿ 𝑏 = 𝑏 o 𝑏 = −𝑏? ¿porqué?
➢Si 𝑏 < 0 entonces ¿ 𝑏 = 𝑏 o 𝑏 = −𝑏? ¿porqué?

5. Resolvamos ahora algunas ecuaciones simples con valor absoluto
• Hallar los valores de 𝑥 que verifiquen las siguientes igualdades:
a) 𝑥 = 125 b) 𝑥 = −
2
5
c) 𝑥 + 4 = 15
Respuestas:
a) Los valores posibles son: 𝑥 = 125 ó 𝑥 = −125. (𝑆 = −125 , 125 )
Podemos pensar esta igualdad de la siguiente manera: ¿Cuáles son los números cuya
su distancia al cero es 125?
b) No existe ningún valor posible para 𝑥 de manera tal que su valor absoluto sea un
número negativo ya que el valor absoluto de un número es positivo o cero. ( 𝑆 = ∅)
c) Para resolver esta igualdad vamos a usar la definición de valor absoluto

6. 𝑥 + 4 = 15 ⟺ ൜
𝑥 + 4 = 15 𝑠𝑖 𝑥 + 4 ≥ 0
− 𝑥 + 4 = 15 𝑠𝑖 𝑥 + 4 < 0
⟺ ቊ
𝑥 = 11 𝑠𝑖 𝑥 ≥ −4
𝑥 + 4 = −15 𝑠𝑖 𝑥 < −4
⟺
⇔ ቊ
𝑥 = 11 𝑠𝑖 𝑥 ≥ −4
𝑥 = −19 𝑠𝑖 𝑥 < −4
⟺ 𝑥 = 11 ó 𝑥 = −19.
➢ Si verificamos estos números en la ecuación observamos que efectivamente ambos son soluciones.
Teniendo en cuenta que :
Si consideramos 𝑎 = 𝑥 + 4 obtenemos que: 𝑥 + 4 = ቊ
𝑥 + 4 𝑠𝑖 𝑥 + 4 ≥ 0
− 𝑥 + 4 𝑠𝑖 𝑥 + 4 < 0
y volviendo a la ecuación 𝑥 + 4 = 15 , podemos escribir esto como:
𝑎 = ቊ
𝑎 𝑠𝑖 𝑎 ≥ 0
−𝑎 𝑠𝑖 𝑎 < 0

7. Algunas propiedades del Valor Absoluto
1) 𝑥 ≥ 0 ∀𝑥 ∈ 𝑅.
2) 𝑥 = 0 ⟺ 𝑥 = 0.
3) 𝑥 = 𝑑, 𝑑 > 0 ⟺ 𝑥 = 𝑑 ó 𝑥 = −𝑑.
4) 𝑥 = −𝑥
5) 𝑥 = 𝑦 ⇔ 𝑥 = 𝑦 ó 𝑥 = −𝑦.
6) 𝑥 ∙ 𝑦 = 𝑥 ∙ 𝑦
7)
𝑥
𝑦
=
𝑥
𝑦
, 𝑦 ≠ 0
8) 𝑥 2
= 𝑥2
, ∀𝑥 ∈ ℝ
9) 𝑥2 = 𝑥

8. ➢Usando propiedades (en particular la propiedad 3 anterior) podemos resolver la
ecuación 𝑥 + 4 = 15 de una manera más simple, sin tener que usar la
definición de valor absoluto:
𝑥 + 4 = 15 ⇔ 𝑥 + 4 = 15 ó 𝑥 + 4 = −15 ⇔ 𝑥 = 11 ó 𝑥 = −19
➢¿Cómo podríamos resolver la ecuación 3𝑥 − 1 = 𝑥 + 1 Usando propiedades?
La propiedad 5 nos permite resolverla de la siguiente manera:
3𝑥 − 1 = 𝑥 + 1 ⇔ 3𝑥 − 1 = 𝑥 + 1 ó 3𝑥 − 1 = − 𝑥 + 1
⇔ 3𝑥 − 1 = 𝑥 + 1 ó 3𝑥 − 1 = −𝑥 − 1 ⇔ 2𝑥 = 2 ó 4𝑥 = 0
⇔ 𝑥 = 1 ó 𝑥 = 0. 𝑆 = 0, 1 . (verificar que ambos valores satisfacen la igualdad)

9. ➢ La propiedad 9) nos permite resolver algunas ecuaciones en las que interviene
un factor cuadrático, por ejemplo:
𝑥 + 5 2 + 1 = 10 ⇔ 𝑥 + 5 2 = 9 ⇔ 𝑥 + 5 2 = 9 ⇔ 𝑥 + 5 = 3
⇔ 𝑥 + 5 = 3 ó 𝑥 + 5 = −3 ⇔ 𝑥 = −2 ó 𝑥 = −8
Aquí también hemos usado la propiedad 3: 𝑥 = 𝑑 ⟺ 𝑥 = 𝑑 ó 𝑥 = −𝑑

10. Pensemos ahora en lo siguiente: ¿Cuáles son todos los números reales que verifican
que su valor absoluto es menor a 2?
Lo que realizamos anteriormente lo podemos expresar en símbolos mediante una
inecuación:
𝒙 < 𝟐 ⇔ 𝒙 ∈ −𝟐 , 𝟐 .
Si interpretamos esto con la idea de distancia, estamos buscando aquellos
“números cuya distancia al cero es menor a 2”.
Si graficamos esta situación en la recta numérica obtenemos el intervalo (−2 , 2):
➢ Vamos a resolver esta inecuación a partir de la definición de valor absoluto:
𝑥 < 2 ⇔ ቊ
𝑥 < 2 𝑠𝑖 𝑥 ≥ 0
−𝑥 < 2 𝑠𝑖 𝑥 < 0
⇔ ቊ
𝑥 < 2 𝑠𝑖 𝑥 ≥ 0
𝑥 > −2 𝑠𝑖 𝑥 < 0
⇔
⇔ 𝑥 ∈ 0,2 ó 𝑥 ∈ (−2,0) ⇔ 𝑥 ∈ 0,2 ∪ (−2,0) ⇔ 𝑥 ∈ (−2,2)..

11. ➢ Intentemos ahora hallar los valores de 𝑥 cuya distancia al cero es
mayor o igual a 3.
Es decir, tenemos que resolver la inecuación 𝒙 ≥ 𝟑
Si lo representamos en la recta numérica , podemos marcar primero los valores
de 𝑥 cuya distancia al cero es exactamente 3, es decir, 3 y -3, y luego pensamos
en aquellos valores cuya distancia al cero es mayor a 3:
Entonces la solución es:
𝑆 = −∞, −3 ∪ [3, +∞)

12. Más propiedades de valor absoluto
10) ∀𝑎 > 0, 𝑥 ≤ 𝑎 ⟺ −𝑎 ≤ 𝑥 ≤ 𝑎 ⇔ 𝑥 ∈ −𝑎, 𝑎 .
11) 𝑥 ≥ 𝑎 ⟺ 𝑥 ≥ 𝑎 ∨ 𝑥 ≤ −𝑎 ⇔ 𝑥 ∈ −∞, −𝑎 ∪ [𝑎, +∞).
12) Desigualdad triangular: 𝑥 + 𝑦 ≤ 𝑥 + 𝑦 .
13) 𝑥 − 𝑦 = 𝑦 − 𝑥 .
Estas propiedades nos permiten resolver las inecuaciones con valor absoluto de
una manera mas simple.
Por ejemplo, para resolver 𝑥 − 3 ≤ 5 usamos la propiedad 10: (cuidado que aquí
tenemos que reemplazar 𝑥 por 𝑥 − 3)
𝑥 − 3 ≤ 5 ⟺ −5 ≤ 𝑥 − 3 ≤ 5 ⟺ −2 ≤ 𝑥 ≤ 8 ⟺ 𝑥 ∈ −2, 8 .

13. • Otro Ejemplo: Resolver usando propiedades la inecuación:
3𝑥 − 1 ≥ 2
Usamos la propiedad 11: 𝑥 ≥ 𝑎 ⟺ 𝑥 ≥ 𝑎 ∨ 𝑥 ≤ −𝑎
3𝑥 − 1 ≥ 2 ⟺ 3𝑥 − 1 ≥ 2 ó 3𝑥 − 1 ≤ −2
⟺ 3𝑥 ≥ 3 ó 3𝑥 ≤ −1 ⟺ 𝑥 ≥ 1 ó 𝑥 ≤ −
1
3
⟺ 𝑥 ∈ −∞, −
1
3
∪ [1, +∞) .
𝑆 = −∞, −
1
3
∪ [1, +∞)

14. El valor absoluto como distancia
¿Cómo podemos calcular la distancia que hay entre dos números de la recta
numérica? Por ejemplo, ¿Cuál es la distancia entre 3 y 8?
Si observamos en la recta vemos que la distancia es 5.
¿Cuál es la distancia entre - 4 y 4?
La distancia es 8.
¿Cómo podemos calcular la distancia entre dos números reales?
Si hacemos la diferencia entre ambos números podríamos obtener un valor negativo,
sin embargo el valor absoluto de la diferencia nos daría un número positivo, es por
ello que se define “la distancia entre dos números reales 𝒙 e 𝒚" como:
𝒅(𝒙, 𝒚) = 𝒙 − 𝒚 = 𝒚 − 𝒙

15. ✓También nos permite interpretar la expresión 𝑥 − 3 como la distancia entre 𝑥 y 3.
Por lo tanto la inecuación 𝑥 − 3 ≤ 5 se puede interpretar como:
“ todos los puntos de la recta real cuya distancia a𝐥 𝟑 es menor o igual a 5”.
✓ La definición de distancia permite expresar que la distancia de un
número 𝑥 al cero es :
𝒅(𝒙, 𝟎) = 𝒙 − 𝟎 = 𝒙
como lo habíamos interpretado inicialmente.
Una manera de resolver esta inecuación “en forma geométrica” es ubicando
al 3 como nuestro “centro” y moviéndonos cinco unidades a la derecha y
cinco unidades a la izquierda del 3, de esta manera obtenemos los puntos
que están a una distancia de cinco unidades del 3 (estos son -2 y 8) . A partir
de allí y volviendo a interpretar la inecuación podemos marcar los valores
cuya distancia al 3 es menor o igual a 5, y obtenemos que la solución es el
intervalo −2, 8

16. ➢La expresión 𝑥 + 9 se puede interpretar como la distancia entre 𝑥 y −9
Por lo tanto la inecuación 𝑥 + 9 > 10 , que es equivalente a:
𝑥 − (−9) > 10
Se interpreta geométricamente como todos los puntos de la recta real cuya
distancia al −𝟗 es mayor a 10.
Para resolver la inecuación por medio de esta interpretación
geométrica, ubicamos al −9 como nuestro “centro” y
moviéndonos 10 unidades a la derecha y 10 unidades a la
izquierda del −9 obtenemos los puntos que están a una
distancia de 10 unidades del −9 (estos son -19 y 1) . A partir de
allí y volviendo a interpretar la inecuación podemos marcar los
valores cuya distancia al − 9 es mayor o igual a 10, y obtenemos
que la solución es el intervalo (−∞, −19) ∪ (1, +∞) .

17. • En general:
𝒙 − 𝒂 ≤ 𝒅 se puede interpretar geométricamente como los valores de 𝑥 cuya
distancia al centro 𝒂 es menor o igual que el radio 𝒅 (o semiamplitud d), por lo que
se obtiene 𝑥 ∈ −𝑑 + 𝑎, 𝑑 + 𝑎 . Gráficamente:
Observación 1: si tenemos 𝑥 + 𝑎 ≤ 𝑑 , el centro es el opuesto de 𝑎, es decir, −𝑎.
Observación 2: Para interpretar en forma geométrica una inecuación como 4𝑥 − 2 ≤ 8, es
necesario que tengamos a 𝑥 sin ningún factor multiplicando, por lo tanto podemos sacar factor
común 4 y modificar nuestra inecuación de la siguiente manera:
4𝑥 − 2 ≤ 8 ⇔ 4 𝑥 −
1
2
≤ 8 ⇔ 4. 𝑥 −
1
2
≤ 8 ⇔ 𝑥 −
1
2
≤
8
4
⇔ 𝑥 −
1
2
≤ 2
Entonces la inecuación se puede interpretar geométricamente como” son todos los números cuya
distancia al
1
2
es menor o igual que 2, 𝑆 = −
3
2
,
5
2
(centro
1
2
y radio 2)

18. • 𝑥 − 𝑎 ≥ 𝑑 ⟺ 𝑥 ≤ −𝑑 + 𝑎 ∨ 𝑥 ≥ 𝑑 + 𝑎 ⟺ 𝑥 ∈ ൫−∞, ሿ
−𝑑 + 𝑎 ∪ [𝑑 + 𝑎, )
∞
• 𝑥 − 𝑎 > 𝑑 ⟺ 𝑥 < −𝑑 + 𝑎 ∨ 𝑥 > 𝑑 + 𝑎 ⟺ 𝑥 ∈ (−∞, )
−𝑑 + 𝑎 ∪ 𝑑 + 𝑎, ∞
• 𝑥 − 𝑎 < 𝑑 ⟺ −𝑑 < 𝑥 − 𝑎 < 𝑑 ⟺ −𝑑 + 𝑎 < 𝑥 < 𝑑 + 2 ⟺ 𝑥 ∈ −𝑑 + 𝑎, 𝑑 + 𝑎

19. Ejercicio 1: Resolver la inecuación: 𝑥 + 3 2 + 1 ≤ 5
𝑥 + 3 2 + 1 ≤ 5 ⇔ 𝑥 + 3 2 ≤ 4 ⇔ 𝑥 + 3 2 ≤ 4 ⇔
⇔ 𝑥 + 3 ≤ 2 ⇔ 𝑥 ∈ −3 − 2, −3 + 2 ⇔ 𝑥 ∈ −5 , −1 .
Ejercicio 2: Encontrar el conjunto solución de la inecuación 4𝑥 − 2 > 1 por medio de:
a) Definición de Valor Absoluto
b) Propiedades de Valor Absoluto.
c) Interpretación geométrica del Valor Absoluto.