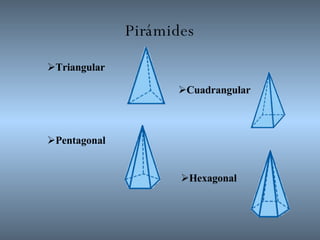
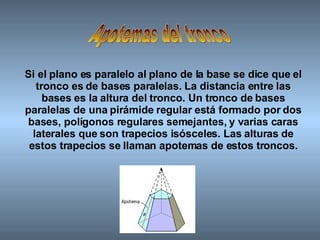
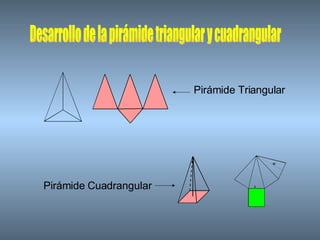
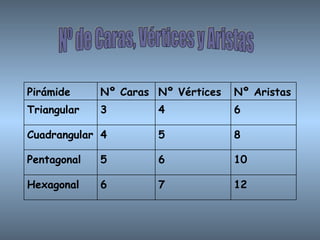
Este documento proporciona información sobre las pirámides, un tipo de poliedro. Describe las características de las pirámides regulares y cómo se clasifican según la forma de su base, como triangular, cuadrangular o pentagonal. También explica cómo calcular el área lateral, área total y volumen de una pirámide.

1. Clasificación de los poliedros Poliedros Regulares Prismas Pirámides Tetraedro Cubo o hexaedro Octaedro Dodecaedro Icosaedro Triangular Cuadrangular Pentagonal Hexagonal Triangular Cuadrangular Pentagonal Hexagonal

3. Piramides La pirámide es un poliedro que tiene por base un polígono y por caras laterales varios triángulos con un vértice en común. La altura de la pirámide es la distancia del vértice a la base.

5. Pirámide Regular Una pirámide es regular si su base es un polígono regular y el vértice se proyecta (cae perpendicularmente) sobre el centro de la base. En una pirámide regular las caras laterales son triángulos isósceles cuyas alturas se llaman apotemas de la pirámide.

6. Tronco de Pirámide Un tronco de pirámide es el poliedro comprendido entre la base de la pirámide y un plano que corta a todas las aristas laterales.

7. Si el plano es paralelo al plano de la base se dice que el tronco es de bases paralelas. La distancia entre las bases es la altura del tronco. Un tronco de bases paralelas de una pirámide regular está formado por dos bases, polígonos regulares semejantes, y varias caras laterales que son trapecios isósceles. Las alturas de estos trapecios se llaman apotemas de estos troncos. Apotemas del tronco

8. Desarrollo de la pirámide triangular y cuadrangular Pirámide Cuadrangular Pirámide Triangular

9. Nº de Caras, Vértices y Aristas 12 7 6 Hexagonal 10 6 5 Pentagonal 8 5 4 Cuadrangular 6 4 3 Triangular Nº Aristas Nº Vértices Nº Caras Pirámide

10. Área Lateral de una Pirámide En una pirámide regular se cumple que: El área lateral es igual al producto del semiperímetro de la base por la longitud de la apotema de la pirámide. A LATERAL = semiperímetro · apotema

11. Área total de una Pirámide En una pirámide cualquiera se cumple que : El área total esta determinada por la suma de las áreas de las caras laterales y el área de la base A TOTAL = A LATERAL + A BASE

12. Volumen de una Pirámide El volumen de una pirámide es igual a un tercio del volumen del prisma. V PIRÁMIDE = 1 / 3 V PRISMA V PIRÁMIDE = 1 / 3 (A BASE ) (altura)