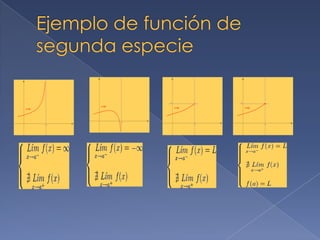
Este documento describe tres tipos principales de discontinuidad de una función: discontinuidad evitable, discontinuidad esencial y discontinuidad de primera especie. La discontinuidad evitable ocurre cuando la función tiene un valor diferente en un punto aunque su límite existe en ese punto. La discontinuidad esencial ocurre cuando los límites laterales no coinciden, son infinitos o no existen. La discontinuidad de primera especie incluye salto finito, salto infinito y discontinuidad asintótica dependiendo de si los límites laterales son finitos o infinitos

1. TIPOS DE DISCONTINUIDADUNIDAD 3 CONTINUIDADING. MA.YAZMÍN MUÑOZ LOZANO

2. La discontinuidad de una función puede ser clasificada en:

3. Discontinuidad evitable:Si una función tiene límite en un punto, pero la función en ese punto tiene un valor distinto.O no existe

4. Se dice que la discontinuidad es evitable, asignando a la función, en ese punto, el valor del limite:

5. Ejemplo de función evitable

6. Discontinuidad esencialSe dice que una función presenta una discontinuidad esencial cuando se produce algunas de las siguientes situaciones:Existen los límites laterales pero no coinciden.Alguno de los límites laterales o ambos son infinitos. No existe alguno de los límites laterales o ambos.

7. Discontinuidad de primera especieEn este tipo de discontinuidad existen tres tipos:De salto finito Existen el límite por la derecha y por la izquierda del punto, su valor es finito, pero no son iguales:

8. A este tipo de discontinuidad de primera especie se le llama salto finito, y el salto viene dado por:

9. Ejemplos de funciones de salto finito

10. De salto infinitoSi uno de los límites laterales es infinito y el otro finito, tanto si el limite por la izquierda es finito y el de la derecha infinito:

11. Como en el caso de que el límite por la izquierda sea infinito y por la derecha finito:Se dice que discontinuidad es de salto infinito

12. Ejemplo de funciones de salto infinito

13. Discontinuidad asintóticaSi los dos limites laterales de la función en el punto x0 son infinitos:A este tipo de discontinuidad de primera especie se le llama discontinuidad asintótica, siendo x = a la asíntota.

14. Ejemplo de funciones asintótica

15. Discontinuidad de segunda especieSi la función no existe en uno de los lados del punto, o no existen alguno, o ambos, de los limites laterales de la función en ese punto, se dice que la función presenta una discontinuidad de segunda especie en ese punto.

16. Ejemplo de función de segunda especie