Geometría 2 delta

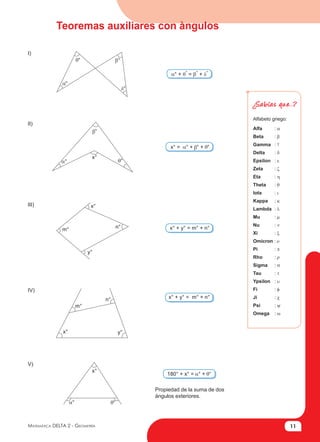
11
Matemática Delta 2 - Geometría
I)
II)
III)
x° = ° + ° + °
° + θ° = β° + δ°
Propiedad de la suma de dos
ángulos exteriores.
IV)
V)
180° + x° = ° + °
x° + y° = m° + n°
m°
x°
n°
y°
x°
°
° °
m°
n°
x° y°
x°
° °
¿Sabías que...?
°
°
β°
δ°
Alfabeto griego:
Alfa :
Beta :
Gamma :
Delta :
Epsilon :
Zeta :
Eta :
Theta :
Iota :
Kappa :
Lambda :
Mu :
Nu :
Xi :
Omicron :
Pi :
Rho :
Sigma :
Tau :
Ypsilon :
Fi :
Ji :
Psi :
Omega :
x° + y° = m° + n°
Teoremas auxiliares con àngulos

18
4 Calcula el valor de β.
3 Calcula el valor de .
5θ
6θ 120° 10°
Resolución:
60°
7β
2β
20°
Resolución:
7 En la figura, halla el valor de x. 8 Halla el valor de x.
6 En la figura que se muestra, determina el valor de x.
5 En la figura que se muestra, determina el valor de .
Resolución: Resolución:
120°
70°
A
B
C
a
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
70o
B
3x
A
40º + 2x
C
140°
2x 6x x 126°

19
10 Los lados AB y BC de un triángulo ABC miden
7 cm y 11 cm y AC mide el doble de uno de ellos.
¿Cuánto es el perímetro del triángulo?.
12 Determina m BMC.
13 Del gráfico, encuentra el valor de x.
11 Determina m BCA.
9 Los lados de un triángulo isósceles miden 4 cm y
10 cm. Calcula el perímetro del triángulo.
Resolución:
Resolución:
Resolución:
120°
A C D
80°
3
B
Resolución:
B
A
M
C
4β 4β
2β 20°
14 Encuentra el valor de x.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
x
20°
50º
x
60º
100º

20
16 Halla la medida del mayor ángulo de un triángulo
isósceles, si los ángulos iguales miden 56°.
17
Las medidas de los ángulos internos de un
triángulo son proporcionales a 2, 4 y 6. ¿Cuáles
son sus medidas?
18 Lasmedidasdelosángulosinternosdeuntriángulo
están en proporción a 4, 6 y 8. Calcula el menor
de los ángulos internos de dicho triángulo.
19 En la figura, determina el valor de x. 20 Determina el valor de x en el gráfico.
15 Halla la medida del menor ángulo interno de un
triángulo rectángulo isósceles.
Resolución:
Resolución:
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
x
40º
140º
B
A C
D
10º
80º
x
B
A C
D

21
1
2 5
4
3 6
De las siguientes afirmaciones, escribe V si es
verdadera o F si es falsa.
I) Triángulo escaleno: lados con diferentes
longitudes.
II) Triángulo isósceles: si sus tres lados son de
igual longitud.
III) Triángulo equilátero: si tiene dos lados de
igual longitud.

A VVV
B FVV
C FVF
D VFF
E FFF
Señala el lado mayor del triángulo PQR.
68°
64° 48°
P R
Q
1. Ángulos de medidas iguales a) isósceles
2. Ángulos de medidas diferentes b) equilátero
3. Dos ángulos de medidas iguales c) escaleno
Relaciona; luego, marca la alternativa correcta.

A 1b, 2c, 3a
B 1c, 2b, 3a
C 1b, 2a, 3a
D 1a, 2b, 3c

E 1c, 2a, 3b
En un triángulo dos de sus lados miden 3 cm y
7 cm, si el tercer lado del triángulo mide el triple
de uno de ellos, halla el perímetro del triángulo.
A 22 cm
B 22 o 29 cm
C 29 cm D Faltan datos
E N. A.
A PQ
B QR
C PR D Faltan datos
E N. A.
Determina el valor de x + y.
50°
x
65°
y
80°
60°
Se tiene un triángulo isósceles cuyos lados miden
5 cm y 12 cm. ¿Cuánto mide el perímetro del
triángulo?

A 31 cm
B 19 cm
C 30 cm
D 31 o 19 cm

E Ese triángulo es imposible.

A 115°
B 103°
C 105°
D 145°
E 95°
Nivel I
Practica y demuestra

22
8
11
9 12
7 10
En la figura, calcula m HQP, si la medida del
ángulo PQR es 120°.
Determina el valor de m + n.
Si la medida de uno de los ángulos de un triángulo
rectángulo es
4
5
de la medida del otro. ¿Cuánto
mide el ángulo menor?
En un triángulo ABC, la medida del ángulo B es el
doble del ángulo A y el ángulo C es igual a la suma
de A + B. ¿Cuánto mide el ángulo menor?
La suma de las medidas de los ángulos B y C de
un triángulo ABC es 105°. Si la medida del ángulo
A excede a la del ángulo C en 40°. ¿Cuánto es la
medida del ángulo B?
50°
m
120°
20°
70°
n
En la figura se cumple que si AB = BC, BP = BQ,
halla el valor de x.
B
A
P
x
Q
C
30°

A 40°
B 50°
C 60°
D 70°
E N. A.

A 100°
B 101°
C 99°
D 180°
E N. A.

A 30°
B 40°
C 45°
D 60°
E 180°

A 40°
B 80°
C 70°
D 60°
E 75°

A 40°
B 30°
C 50°
D 80°
E N. A.

A 30°
B 40°
C 20°
D 50°
E N. A.
Q
P
H
R
40°
Nivel II

23
En la figura, determina el valor de x.
En la figura se cumple que AB = BC. Calcula el
valor de x.
x
75°
2b
b
En la figura, encuentra el valor de x.
3x
4x
4x
3x
4x
En la figura se cumple que BD = PD. Halla el valor
de x.
En la figura se cumple que AB = PC. Calcula el
valor de x.
B
5x
P
x
7x
x
C
A
Si en la figura se cumple que α + θ = 70°.
Determina el valor de x, si AP = PB y BQ = QC.

A 40°
B 50°
C 30°
D 60°
E 70°

A 30°
B 80°
C 75°
D 45°
E 60°

A 8°
B 10°
C 12°
D 15°
E 20°

A 10°
B 20°
C 30°
D 40°
E 50°

A 60°
B 65°
C 70°
D 75°
E 80°

A 15°
B 10°
C 250°
D 40°
E 45°
B
80°
60°
2x
A C
Q
P D
B
A
x
P
H
C
B
A
P Q
C
x
α
13
14
15
16
17
18

24
21
20
19
22
23
24
En la figura, encuentra el valor del complemento
de x sumado al suplemento de θ.
105°
81°
x
θ
3θ

A 160°
B 165°
C 170°
D 175°
E 189°
En el gráfico, halla el valor de x si el triángulo ABC
es equilátero.
A C
B
x
Si dos lados de un triángulo tienen como longitud
7 u y 2 u. Encuentra el valor del tercer lado que no
sea ni el máximo ni mínimo valor entero.

A 6 u
B 8 u
C 7 u
D 9 u
E 10 u
Dos lados de un triángulo suman 22 u. Determina
el mayor valor entero que puede tomar la altura
relativa al tercer lado.

A 9 u
B 11 u
C 10 u
D 12 u
E 13 u
Clasifica al triángulo ABC.
3x
M
A
2x 45°
E

A Acutángulo

B Isósceles

C Triángulo rectángulo
D Triángulo escaleno

E Más de una es correcta
Calcula el valor de x, si el triángulo ABC es
equilátero.
B
Q
C
A
P
x

A 30°
B 70°
C 60°
D 80°
E 50°

A 30°
B 60°
C 70°
D 80°
E 50°
Nivel III

Tema
25
2
Líneas notables en el triángulo
M
A
M
N
B
B
O
O
El nombre ceviana
fue introducido por
M.A. Poulain, que
lo utilizó en honor
a Giovanni Ceva,
quien en 1678
formuló un teorema
que lleva su nombre,
este teorema da la
condición necesaria
y suficiente para
que tres cevianas se
corten en un punto.
El haber conocido el triángulo nos permite empezar a asociarlo con otras figuras.
Lo puedes asociar a líneas, circunferencias, otros polígonos, etc. En este capítulo
empezaremos a ver la asociación que se puede dar con segmentos a los cuales
llamaremos cevianas.
Ceviana es un segmento de recta que une un vértice de un triángulo con el lado opuesto
a este, o con su prolongación; determinando, de esa manera, la posibilidad que haya una
ceviana interior y una ceviana exterior. También se la conoce como transversal angular.
Gráficamente:
B
A D C E
Para el triángulo ABC:
BD: Ceviana interior
BE: Ceviana exterior
Como verás no le hemos dado ninguna condición especial a esta ceviana; pero cuando
esto ocurre dicha ceviana toma nombre. Existen diversos tipos de cevianas notables. Sin
embargo, en este grado analizaremos solo a dos: la bisectriz y la altura.
Cevianas notables
Bisectriz
Una bisectriz es una ceviana que «biseca» al ángulo (de allí su nombre), a partir del cual
es trazada, determinando de esa manera dos ángulos congruentes. La bisectriz puede
ser interior o exterior.
A C
D
B
En el gráfico, como m ABD = m DBC, entonces BD es bisectriz interior.
Q
R
P S
Se nota en el siguiente gráfico que QS es una bisectriz exterior.
¿Sabías que...?
Importante
OM y ON son
trisectrices
°
°
°
°
°
OM: bisectriz
A
°
°
°
°

26
Un punto notable
es un punto donde
concurren cevianas
notables.
Observa
• Bisectriz en inglés
es bisector.
• Incentro en inglés
es incenter.
• Excentro en inglés
es excenter.
Un triángulo tiene un
único incentro pero
tres excentros.
¿Sabías que...?
Observa
Altura
Una altura es una ceviana perpendicular al lado hacia donde esta es relativa. Esta ceviana
puede ser interior o exterior dependiendo del tipo de triángulo.
B
A C
H
B
H A
C
Cuando las cevianas se intersecan generan puntos, y dependiendo del tipo de ceviana
estos puntos pueden ser singulares, normalmente a estos puntos se le denominan puntos
notables.
Como en este capítulo estamos estudiando a la bisectriz y a la altura, veamos ahora qué
puntos notables se asocian de ellas.
Incentro y excentro
El incentro es el punto de concurrencia de las tres bisectrices interiores de un triángulo.
En el gráfico, tanto AD, BF y CE son bisectrices.
Incentro
del ABC
El excentro es el punto de concurrencia de dos bisectrices exteriores y una bisectriz
interior.
En el gráfico, BD y CE son bisectrices exteriores. AF es bisectriz interior.
E
F
D
B
A
C
Altura interior
Altura exterior
Excentro
del ABC
relativo a BC
A
F
C
D
B
E

27
El símbolo frecuente
para indicar la altura
es la «h», debido
a que en inglés la
palabra para la altura
es height.
Ángulos
suplementarios
Son dos ángulos
cuya suma de
medidas es 180°.
Ángulos
complementarios
Son dos ángulos
cuya suma de
medidas es 90°.
Recuerda
Ortocentro
Es el punto de concurrencia de las tres alturas de un triángulo. Su ubicación puede ser en
la región interior, exterior o en el mismo triángulo, eso va a depender del tipo de triángulo.
Será interior si el triángulo es acutángulo, exterior si el triángulo es obtusángulo, y se
ubicará en el mismo triángulo si es triángulo rectángulo. Veámoslo gráficamente.
Ortocentro
Ortocentro
Ortocentro
Ángulos formados por cevianas notables
Existen teoremas que relacionan ángulos y medidas angulares a partir de las cevianas
que hemos estudiado.
Ángulos en el incentro y excentro
a = b
x = 90° +
θ°
2
B
E
A F
C
D
donde I: incentro
¿Sabías que...?
A
O
H C
T
B
x
I
B
A C
α°
α°
β°
β°
θ°

28
I: incentro del
triángulo ABC
• Incentro
Punto interior
donde concurren
las bisectrices
interiores.
• Ortocentro
Punto de
concurrencia de
las alturas.
Recuerda
También se cumple:
Observa
a = b
x = 90° –
θ°
2
a = b
x =
θ°
2
Ángulos en el ortocentro
a = b
x = 180° – θ°
a = b
x = 180° – θ°
E: excentro
E: excentro
H: ortocentro
H: ortocentro
2x x
¿Sabías que...?
B
C
A
I
x
E
B
D
H
A C
θ°
A
P
C
T
x
H
B
θ°
θ°
θ° α° α°
B
A
C
x
E
β°
β°
θ°
α°
α°
B
E
x
C
A
β°
β°
θ°
α°
α°

29
Observa
No olvides
Resolución:
Como CM es bisectriz, m ACM = m MCB = β°
En el triángulo ABC:
Calcula el valor de x, si CM es bisectriz.
Entonces…
En el triángulo MBC: x + 40° + 30° = 180°
x = 110°
80° + 40° + 2β° = 180°
β° = 30°
C
Resolución:
Como AB = AC, entonces el triángulo ABC es isósceles, por lo tanto:
m ACB = m ABC = 70°
Al ser BH altura, entonces el triángulo BHC es rectángulo. Así:
x + 90° + 70° = 180°
x = 20°
Se observa que en el triángulo ABC, tanto AE como CE son bisectrices, la primera
interior y la segunda exterior. Por lo tanto, E es excentro del triángulo ABC. Por
teorema:
Resolución:
x =
80°
2
⇒ x = 40°
En la figura, AB = AC, y BH es altura. Halla el valor de x.
B
A
M
CM es bisectriz
x
a = b
x =
β°
2
θ° α°
α°
θ°
β°
β°
β°
80°
x
80°
x
B E
A
C

Rpta. 110°

Rpta. 20°

Rpta. 40°
C
B
M
A
x
80°
β
40°
x
40°
A
B
C
H
70°
B
C
H
x
1
2
3
Ejercicios resueltos

30
No olvides
Recuerda
Observa
Resolución:
Por teoría E es excentro del triángulo
ABC. Sabemos que:
En el gráfico, I es el incentro del triángulo rectángulo. Calcula el valor de x.
Resolución:
Por dato del ejercicio, I es incentro del triángulo ABC, por lo tanto AI y CI son
bisectrices interiores.
Por teorema, tenemos:
θ° = 90° +
90°
2
⇒ θ° = 135°
Por otro lado, θ° y x forman un par lineal, por lo tanto son suplementarios.
θ° + x = 180° ⇒ x = 45°
En la figura, halla el valor de x.
Resolución:
En la figura podemos notar fácilmente que H es el ortocentro del ABC.
Por teorema de medida de ángulos en el
ortocentro:
2x + 3x = 180°
x = 36°
B
A
E
C
40°
α
α
x
x
m
x
a + b = 180°
H: ortocentro
a = b
m = 2x
a = b
x = 90° –
°
2
°
°
° °
°
40° = 90° – x
2
⇒ x = 100°
θ°
I
x
B
A C
α β
α β
α° β°
β°
α°

Rpta. 36°

Rpta. 45°

Rpta. 100°
α
β
α β
I
x
B
A C
B
A C
2x
3x
E
a
b
A
H
B
C
B
A C
3x
E
2x
3x
H
4
5
6

31
Síntesis
Modela y resuelve
B
A D C
si a° = b°
BD: bisectriz
B
A H C
si = 90°
BH es altura
m°
x
I
b° a°
a a
a
a
a
b
b
a
x = 90° +
m°
2
m°
2
m°
x
x =
m
2
x
m°
x = 90° –
E: excentro
E
E
E: excentro
I: incentro
H: ortocentro
m°
x
x = 180° – m°
H
2 Construye un triángulo rectángulo ABC recto en B
y traza la altura relativa al lado AC.
Resolución:
1 Construye un triángulo acutángulo ABC y traza la
altura relativa al lado AC.
Resolución:
Líneas notables en el triángulo

32
3 Indica verdadero V o falso F.
- El baricentro es el punto de intersección de las
medianas.
- El ortocentro es el punto de intersección de las
alturas.
- El circuncentro es el punto de corte de las
bisectrices interiores.
4 Calcula el valor de x, si CM es bisectriz.
M
A
B
C
40°
x
80o
Resolución:
Resolución:
Rpta. Rpta.
6 Determina el valor de x, si ABC es equilátero y
CH es altura.
5 Determina el valor de x, si AM es bisectriz.
A
B C
M
40° 60°
x
B
H
A
x
C
8 Indica el valor de x, si AM es bisectriz.
7 Indica el valor de x, si AM y CM son bisectrices.
B
M
x
A C
Resolución:
B
M
C
80°
A
x
Resolución:
Rpta.
Rpta.
Rpta.
Rpta.

33
10 Halla el valor de α, si BM es bisectriz.
9 Halla el valor de x, si BH es altura.
B
x
50°
A
H
C
B
A
M
C
2a–30°
a
12 Encuentra el valor de m ABM, si BM es bisectriz.
11 Encuentra la medida del ángulo ABC, si BM es
bisectriz.
A C
B
M
30°– θ
20°+ θ
2a – 40° a + 10
A
M
C
B
°
Rpta.
Rpta.
Rpta.
Rpta.
13 Calcula el valor de α, si BM es bisectriz. 14 Calcula la suma de las medidas de los ángulos
ABC y CAB, si CP es bisectriz.
55°
P
B
A
C
B
C
M
A
12a – 10° 10a + 80°
Rpta. Rpta.

34
17 Determina el valor de x. 18 Determina el valor de x.
Resolución:
19 Encuentra el valor de x, si QF es bisectriz del
ángulo PQR.
20 En el gráfico, RE es bisectriz exterior del triángulo
ARQ. Encuentra el valor de φ.
Resolución:
Resolución:
16 En un triángulo rectángulo ABC recto en B se traza
la altura BH; la bisectriz del ángulo ABH interseca
a AC en Q, si AC = 20 cm y AQ = 3 cm. Halla la
medida de BC.
Resolución:
B
20°
E
C
A
x
Resolución:
x
I
40°
B
A C
15 En el gráfico, BD es bisectriz interior del ángulo
ABC y BH es altura. Halla el valor de x.
B
A
H
C
D
x
3θ θ
Resolución:
Q
85°
F
R
P
35° x 36° 104°
A
Q
E
R
φ
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.

35
Nivel I
Traza dos bisectrices exteriores en un triángulo
obtusángulo. Indica el excentro.
Determina el valor de x, si AB = AC y BH es altura.
Confecciona un triángulo obtusángulo ABC,
obtuso en el vértice B y traza la altura desde el
vértice A.
Utilizando un transportador, dibuja un ángulo que
mida 150° y mediante compás y regla traza la
bisectriz.
Indica el valor de x, si AH es altura.
B
H
130°
C A
x
40°
x
B
A
H
C
Calcula el valor de x, si BD es bisectriz.
70°
80° x
D
B A
A 45°
B 60°
C 80°
D 70°
E 40°
A 10°
B 15°
C 20°
D 25°
E 30°
A 70°
B 75°
C 80°
D 85°
E 86°
1
4
2 5
3 6

36
De la figura, halla el valor de b, si BM es bisectriz
del ABC.
Del gráfico, encuentra la longitud de BE, si BH es
altura, AE es bisectriz y BF = 10 m.
A 20°
B 30°
C 35°
D 40°
E 50°
A 4 m
B 6 m
C 8 m
D 9 m
E 10 m
B
E
A
H
C
F
B
A M C
140°
2β
β
Determina el valor de a, si BM es bisectriz.
C
M
A B
2a
3a – 15°
A 15°
B 20°
C 25°
D 30°
E 45°
Calcula el valor de , si CP es bisectriz.
A 110°
B 55°
C 35°
D 80°
E 70°
Encuentra el valor de α, si // AC y CP es
bisectriz.
Halla el valor de a, si BP es bisectriz del CBD.
A B D
P
60°
C
B
60°
80°
P
A C
A 120°
B 60°
C 30°
D 90°
E 180°
A 40°
B 30°
C 20°
D 10°
E 15°
Nivel II
7 10
8
11
9 12
B
A C
80° –
+10°
P

37
13 16
14 17
15 18
En el triángulo rectángulo ABC (recto en B) se
traza la altura BH y la bisectriz interior AQ que se
cortan en P, tal que BP = PQ. Determina m BCA.
En un triángulo ABC la m A – m C = 44°. Se
traza la bisectriz interior BD. Calcula la m HAC
siendo AH perpendicular a BD .
A 20°
B 30°
C 40°
D 50°
E 60°
A 41°
B 50°
C 30°
D 44°
E 22°
En la figura, halla a + b, si BD es bisectriz del
ABC.
En el gráfico, encuentra el valor de x.
En el gráfico, determina el valor de x.
En el gráfico, calcula el valor de x en función de a.
m m
5a 4a
x
B
A C
B
A
a
b
E
D C
A 60°
B 75°
C 100°
D 90°
E 80°
A 140°
B 120°
C 160°
D 130°
E 150°
A 60°
B 100°
C 120°
D 80°
E 90°
A a
B
a
2
C 2a
D
a
3
E
3a
2
B
60°
x
A C
B
80°
x
A C
a
a
θ
θ

38
Halla el valor de x.
x
x
D
B
A
C
Encuentra el complemento de x.
B
A C
100°
x
A 30°
B 50°
C 60°
D 80°
E Faltan datos
A 50°
B 140°
C 120°
D 150°
E No existe
19
22
20 23
21 24
Indica el valor de x.
B
A C
x
45°
60°
A 40°
B 30°
C 15°
D 50°
E 25°
Si MN es bisectriz exterior del triángulo ATM,
determina el valor de γ.
T
N
100°
30°
M
A
A 45°
B 30°
C 25°
D 50°
E 35°
Calcula el valor de x.
Si AE y CF son bisectrices, ¿qué punto notable
es I?
A Incentro
B Ortocentro
C Circuncentro D Excentro
E Baricentro
A 30°
B 35°
C 15°
D 20°
E 10°
40°
x
a a a
a b
b
b
b
E
F
A C
B
I
Nivel III

Nombre: n.° de orden: Sección:
Test n.° 1
39
De las afirmaciones, indica el valor de verdad de
cada una.
a) Triángulo acutángulo: si sus tres ángulos
interiores son agudos.
b) Triángulo obtusángulo: si tiene un ángulo
obtuso.
c) Triángulo rectángulo: si tiene un ángulo recto.
La suma de dos ángulos de un triángulo ABC es
140° y su diferencia es 20°. Halla el menor ángulo
externo de dicho triángulo.
Encuentra el valor de x – y.
El perímetro de un triángulo es 96 cm, si un lado
mide 24 cm y los otros están en la relación de 3 a
5. ¿Cuánto mide cada uno de estos lados?
La suma y diferencia de dos ángulos de un
triángulo son 100° y 40°, respectivamente.
Calcula la medida del tercer ángulo de dicho
triángulo.
Determina m CBD.
1 4
2 5
3 6
Marca con una X la alternativa que corresponda a la respuesta.
VVV
A
VFV
C
FVF
B
FFV
D
100°
A
140°
C
120°
B
130°
D
3 y 5
A
27 y 45
C
20 y 45
B
10 y 18
D
30°
A
80°
C
90°
B
70°
D
60°
A
55°
C
40°
B
50°
D
15°
A
20°
C
10°
B
5°
D
50°
y x
70°
2a
a
100°
A C
B
D

40
Encuentra el valor de a, si BP es bisectriz. En el gráfico, determina el valor de x.
Halla el valor de a, si CM es bisectriz. Encuentra el valor de x.
De la figura, calcula el valor de q, si // AC y AP
es bisectriz.
Halla el valor del suplemento de x.
7 10
8 11
9 12
20°
A
60°
C
40°
B
30°
D
60°
A
15°
C
30°
B
20°
D
70°
A
80°
C
40°
B
20°
D
80°
A
40°
C
30°
B
60°
D
40°
A
20°
C
30°
B
10°
D
130°
A
80°
C
140°
B
50°
D
A B
P
2a – 2°
5a – 122°
C
B
70°
50°
M
A C
a
C
B
P
100°
40°
A
q
B
80°
x
A C
a
a θ
θ
x
40°
E
B
A
C
x
I
80°
B
A C

Tema
41
3
Triángulos rectángulos notables
Una pregunta que muchos estudiosos siempre se hicieron era de cómo los antiguos
arquitectos hacían para conseguir con exactitud ángulos rectos. Una de las maneras se
muestra en la imagen de arriba. En una cuerda cerrada de manera equidistante se hacían
12 nudos, y cada uno de ellos delimitaba segmentos que como verás se distribuían en
porciones, formando un triángulo con 3 secciones, 4 secciones y 5 secciones. Por el
teorema de Pitágoras, para cualquier longitud de las secciones, se cumple que:
32 + 42 = 52
En consecuencia, el triángulo construido con dicha cuerda es un triángulo rectángulo.
En este capítulo aprenderemos más sobre los triángulos rectángulos notables. Pero antes
de eso comencemos por definir el teorema de Pitágoras:
c
a
b
Teorema de Pitágoras:
a: Longitud de la hipotenusa
b: Longitud del cateto (1)
c: Longitud del cateto (2)
a2 = b2 + c2
Interpretación geométrica del teorema de Pitágoras
Como vemos en este gráfico, sobre cada uno de los lados del triángulo rectángulo se
pueden construir cuadrados, donde cada uno de sus lados serían recíprocamente lados
de dichos cuadrados. Con la longitud de los lados del triángulo se puede calcular el área
de cada cuadrado, obteniéndose que la suma de las áreas de las regiones cuadradas
construidas sobre los catetos, equivale al área del cuadrado construido sobre la
hipotenusa.
3
4
5 5
25
c
a
b
9
16 4
c2 = a2 + b2
3
5
3
4
En la antigüedad a
los encargados de
medir las porciones
de tierra asignados
a la agricultura se le
llamaban «tensores
de cuerda».
Para obtener ángulos
rectos se usaba la
cuerda de los 12
nudos apoyándose
en el triángulo de 3,
4, 5 también usaban
el triángulo de 6, 8
y 10.
A Pitágoras se
le atribuye la
demostración del
teorema que lleva
su nombre. Sin
embargo, es muy
probable que hayan
sido los alumnos de
la escuela pitagórica
quienes lo hicieron.
¿Sabías que...?
Nota

42
Se llama así a cualquier triángulo rectángulo donde las proporciones de los lados y
las medidas de los ángulos interiores son conocidas. Algunos son exactos y otros
aproximados. En un estudio posterior haremos hincapié en este asunto. Por lo pronto
veamos algunos casos interesantes:
Triángulo rectángulo de 30º y 60º
Se observa que este triángulo rectángulo tiene valores algo complicados; sin embargo,
la relación entre la altura relativa a la hipotenusa y la longitud de esta se encuentra en
relación de 1:4.
60°
30°
2a
a 3
a
45°
45°
b 2
b
b
53°
37°
5k
3k
4k
25k
74°
16°
24k
7k
4a
15°
75°
a ( 6 – 2)a
( 6 + 2)a
k
Nota
60°
45°
30°
45°
k
3
k
3
2
k
2
Observa
15°
4k
k
También se cumple:
75°

43
Recuerda
No olvides
a
c
a = b
a2 + b2 = c2
b
Teorema de
Pitágoras
30°
60° 2k
k
H k 3
5k 4k
3k
37°
53°
4k
k
15°
A
3 cm x
B
3 cm
C
Resolución:
Una posible solución podría ser aplicar directamente el teorema de Pitágoras; sin
embargo, al notar que los catetos son congruentes, podemos asumir que las medidas
de los ángulos agudos son 45º y 45º, en tal caso la hipotenusa es conocida.
En la figura, halla el valor de h.
Resolución:
Se sabe que el triángulo notable de 15º y 75º presenta una relación notable entre la
altura relativa a la hipotenusa, donde:
x =
16 u
4
x = 4 u
53° 30°
20 u x
B
A C

En la figura, calcula el valor de x.
A
B C
3 2 cm
45°
45°
3 cm
3 cm
x = 3 2 cm

Rpta. 3 2 cm

Rpta. 4 u
16 u
h
15°
1
2
3

44
Resolución:
El triángulo ABC, presenta dos ángulos cuyas medidas corresponden a un triángulo
rectángulo notable, pero el triángulo ABC no es un triángulo rectángulo. Entonces vamos
a trazar una altura que nos favorezca, a fin de conseguir triángulos rectángulos. ¿Desde
dónde se debe trazar dicha altura?
La mejor opción es trazarla desde el vértice B. Así que trazaremos la altura BH.
53° 30°
20 u x
B
A C
H
¿Sabías que...?
Recuerda
Luego, resolveríamos el triángulo ABH, es decir, calcularíamos sus lados a partir del
triángulo rectángulo de 37º y 53°.
53° 30°
20 u x
B
A C
H
12 u
16 u
Finalmente como BH = 16 u, entonces en el
triángulo BHC que es un triángulo rectángulo
notable de 30º y 60º, diremos que:
x = 32 u
Resolución:
En el problema anterior vimos una posible solución con el trazo de una altura, en este
ejercicio podríamos hacer lo mismo desde B; sin embargo, aparecería un triángulo de
8º, el cual es un triángulo rectángulo notable, pero no tan conocido.
Una vez más buscaremos una altura que nos favorezca.
En este caso la altura que trazaremos será exterior y desde el vértice A.
Al observar el gráfico, surge la pregunta:
¿Qué conseguimos con este trazo?
Es que ahora ya conocemos la medida
del ángulo ABH que es 45º (Teorema del
ángulo exterior). Y podríamos resolver el
triángulo ABH.
8°
82°
K
7k
5 2 k
x
a = b
x = ° + º
° º

Rpta. 32 u
H
B
A
x
C
8° 37°
6 2 u
6 2 u
B
x
37°
8°
A C
4

45
«Resolver un
triángulo» debe
entenderse como
conocer las medidas
de los lados y de sus
ángulos interiores.
Observa
Finalmente trabajaremos en el triángulo
AHC, donde el cateto AH = 6 u, el cual es
opuesto a un ángulo que mide 37º, y la
variable es la hipotenusa.
Por lo tanto:
x = 10 u
x + 1
x + 2
x
A
B C
Resolución:
Aplicando Pitágoras: x2 + (x + 1)2 = (x + 2)2
Resolviendo: x2 – 2x – 3 = 0
x = 3 y x = –1
Resolución:
En el triángulo rectángulo ABC:
m ABC = 75°
Trazamos desde el vértice A la mediana AM, donde «M» está en BC.
Entonces: MC = 6 (por propiedad de la mediana en triángulos rectángulos).
Luego, el AHM es notable:
∴ AH = 3
Por lo tanto, el valor de x es 3.

Rpta. 10 u

Rpta. 3

Rpta. 3 cm
H
B
A
x
C
8° 37°
6 2u
6 u
45°
6 u
5
6
15°
30°
15°
6 6
6
75°
A
B
H
M
C
x
12 cm
15°
A
B
H
C
x

46
1
2
1
Síntesis
Modela y resuelve
En la figura, calcula el valor de a + b. En la figura, calcula el valor de k – m.
Teorema
de Pitágoras
se cumple:
a2 = b2 + c2
a
b
c
2k
30°
60°
k
3
k
2
k
45°
45°
k
k
75°
h
15°
4 h
Observación
5k
3k
4k
37°
53°
k
k
3
3
k
3
3
2
30°
60° 45°
45°
k k
2
2
k
2
2
Resolución:
a
60°
12 u
b
m k
8 cm
45°
Resolución:
Rpta. Rpta.

47
3 4
5 6
7 8
9 10
Determina la longitud de AD, si CD = 5 u. Determina el valor de BC, si AB = 10 cm.
Encuentra la longitud de BC, si AC = 20 cm.
Encuentra la longitud de PQ, si AC = 5 m.
Halla la longitud de HR, si AB = 10 u.
Si ABC es un triángulo equilátero.
Halla PQ
PR
, si BC = 15 cm, AP = 4 cm.
Resolución:
Resolución:
En la figura, calcula el valor de x. Calcula la longitud de x, si AD = DC.
Resolución:
Resolución:
C
P
B
A
53°
1
5
°
Q
37°
D
A
23°
B
C
C
R
B
x
37°
A
H
53° 30°
60 u x
B
A C
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
R
Q
A
P
C
B
E
37
B
C
A D
x
40 m
30° 15°
A
20
C
B
45°
B
30°
A C

48
En la figura, halla el valor de x, si AD = DC. Halla el valor de x.
En la figura, determina el valor de x. Determina el valor de a + b.
Resolución:
Resolución:
Del gráfico, encuentra el valor de x. Encuentra el valor de x.
Resolución:
Calcula la longitud de AD, si CD = 10 cm. Del gráfico, calcula el valor de x.
Resolución:
Resolución:
Resolución:
B
A C
53°
x
20 cm
2x + 2
B
A C
45°
10 2 cm
45°
b
a
6 u
x
37°
45°
3 cm
x
10 m
53°
37°
30°
12 cm
30°
x
45°
6 2 cm
23°
37°
B
D
C
A
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
8 cm
x
C
A
B
D
60º
37º
12
11
13 14
15 16
17 18

49
Nivel I
1
2 5
3 6
4
En la figura, calcula el valor de a – b.
a
6
37°
b
Halla la medida de HQ, si AB = 24 cm.
En la figura, determina el valor de BC si
AB = 10 m.
30° 45°
B
A C

A 1 u
B 2 u
C 3 u
D 4 u
E 5 u
En la figura, encuentra el valor de CQ, si
AB = 10 mm.
37°
B
Q
A
H
C
30°

A 3 3 mm
B 9 mm
C 6 3 mm
D 6 mm
E 4 mm

A 4 cm
B 6 cm
C 8 cm
D 9 cm
E 12 cm

A 8 2 m
B 10 2 m
C 5 m

D 6 2 m
E 5 2 m
Calcula el valor de x + 3y.
A 6 u
B 6 3 u
C (6 + 6 3) u
D 24 u
E 12 u
30°
A
B
C
x
y
12 u
B
A
H M
Q
15°
15°
C
6 + x
B
A
30°
C
20 cm
A 10 cm
B 4 cm
C 6 cm
D 8 cm
E 3 cm

50
7 10
8
11
9
12
Determina el valor de x.
B
A C
30°
x
6 2 m
15°
Encuentra el valor de x, si AE = ED.
x
60 cm
53°
A E D
C
B
A 30 cm
B 34 cm
C 26 cm
D 28 cm
E 24 cm
Calcula el valor de x, si BE = EC.
6 2 u
B
E
D
C
53°
6 2 u
A
x
A 4 u
B 8 u
C 10 u
D 5 u
E 6 u
A 10 cm
B 12 cm
C 14 cm
D 15 cm
E 12 2 cm
Según el gráfico, halla el valor de x.
x
45°
60° 4 3 cm
B
A
C
A 6 cm
B 6 3 cm
C 4 3 cm
D 6 2 cm
E 3 2 cm
Del gráfico, determina el valor de x.
x
6 u
30° 53°
37°
A 8 u B 10 u C 12 u
D 14 u E 16 u
Encuentra el valor de x.
2 u
x
60°
30°

A 2 u
B 2 3 u
C 3 3 u
D 4 3 u
E N. A.
Nivel II

51
13 16
14 17
15 18
De la figura, halla el valor de x.
x 8 u
53° 30°
A 3 u B 4 u C 5 u
D 6 u E 7 u
20 cm
x + 9
x
7 cm
A 15 cm B 12 cm C 18 cm
D 10 cm E 16 cm
Determina el valor de BC, si AB = 6 2 m.
A 10 m B 5 m C 10 2 m
D 8 m E 4 2 m
De acuerdo a la figura, calcula el valor de x – y.
37°
8 u
x
y
A 2 u B 4 u C 1 u
D 3 u E 5 u
Calcula el valor de x, si BE es bisectriz del
CBM.
8 2 m 16 m
x
45°
A M E C
B
De la figura, halla el valor de x.
A 6 cm B 8 cm C 10 cm
D 6 3 cm E 8 2 cm
B
A C
37°
45°
4
3
cm
60°
x
6 cm
A 10° B 20° C 30°
D 40° E 50°

52
Nivel III
De la figura, determina el valor de x – y.
a20 u
45°
x
y
Del gráfico, halla el valor de x.
Encuentra el valor de m.
x
8 m
45°
32 u
x
37°
30°
3 cm
m
D
A C
30° 45°
B

A 6 m
B 4 2 m
C 8 m
D 4 m
E 1 m
A (4 – 3 ) cm
B (7 – 3 ) cm
C (7 + 3 ) cm D (3 – 3 ) cm
E (8 + 3 ) cm
A 1 u B 2a u C a10 u
D 0 u E 2 u
A
C B
50 cm
x
53°
37°
A 20 cm B 30 cm C 40 cm
D 50 cm E 60 cm
El ABC es equilátero, calcula el valor de x.
8 u
6 u
P
A x C
B
A 6 u B 8 u C 9 u
D 7 u E 5 u
A 5 3 u B 10 2 u C 10 3 u
D 12 3 u E 16 u
19 22
20
23
21
24

Tema
53
4
Congruencia de triángulos
Dos figuras geométricas se dicen que son congruentes, cuando son idénticas en forma
y medidas.
Tomemos a un segmento como ejemplo:
Digamos que tanto el segmento AB como el segmento curvo PQ tienen la misma medida
longitudinal. ¿Eso los convertiría en congruentes? Obviamente la respuesta es NO, ya
que ambos no tienen la misma forma.
Analicemos otra situación con circunferencias:
C1
C2
Y este par de circunferencias… ¿Son congruentes? Tampoco, porque a pesar de tener la
misma forma no tienen el mismo tamaño.
Veamos ahora esta situación:
B
A
C
D
L
L L
Q R
P S
L
Se observa que ambos son cuadrados (misma forma), con la misma longitud de lados
(mismo tamaño). Podemos concluir que ambas figuras son CONGRUENTES.
¿Y por qué no es exacto decir que las figuras son «iguales»?
Para empezar, el término igualdad va asociado normalmente a un número (medida); en
este caso podríamos decir que las medidas son iguales.
Por otro lado, es obvio que las figuras no son iguales porque están formadas por un distinto
conjunto de puntos. En el ejemplo de los cuadrados los vértices del primer cuadrado son
los puntos A, B, C y D; mientras que en el otro son los puntos P, Q, R y S. Por tanto, dichos
cuadrados no son los mismos.
12 cm
A
B
P
Q
12 cm
Si los triángulos
son congruentes.
B
A C
H
a° b°
Q
P R
T
a° b°
Podemos afirmar que
todos los elementos
homólogos o
correspondientes
también miden igual.
Importante
Recuerda
A
P
B
Q
m AB = m PQ
segmento AB
es congruente al
segmento PQ
AB PQ
También
Se lee: el
5 u
5 u
BH = QT

54
Observa
= Se lee: igual a
Se lee: congruente a
<>Se lee: equivalente a
Corolario
Cuando el triángulo
es rectángulo también
se puede decir que
son congruentes; si
cumple que:
El corolario es
una proposición
matemática de
menor jerarquía que
un teorema, ya que
está restringido a
un tipo especial de
figura.
Por definición de congruencia: dos triángulos son congruentes si todas sus medidas,
tanto angulares como laterales son las mismas.
Un caso simbólico es el siguiente par de triángulos.
Criterios para determinar la congruencia de triángulos
Aunque, por definición de congruencia, se afirma que todos los elementos tienen la
misma medida. Sin embargo, hay algunos criterios que determinan la congruencia con
simplemente satisfacer dichas condiciones.
Existen muchos criterios, no obstante los más conocidos son:
1. Lado-ángulo-lado (L - A - L). Dos triángulos son congruentes si consecutivamente
tienen un lado, un ángulo y luego un lado con las mismas medidas.
2. Ángulo-lado-ángulo (A - L - A). Dos triángulos son congruentes si consecutivamente
tienen un ángulo, un lado y un ángulo con las mismas medidas.
H P
F G M N
a° θ° a° θ°
3. Lado-lado-lado (L - L - L). Dos triángulos son congruentes si los tres lados miden
igual.
NOTA: Como puedes notar a veces se suele colocar marcas iguales para indicar que
las medidas de los lados o de los ángulos es la misma.
a°
a°
a°
a°
F
D E R S
T
¿Sabías que...?
Importante
C R
A B P Q
b° b°
B
A C
E D
F
a° θ°
b°
a°
θ°
b°

55
Teoremas que aplican la congruencia
Teorema de la bisectriz. Las perpendiculares trazadas desde un punto de la bisectriz
hacia los lados del ángulo desde el cual se ha trazado la misma, determinan dos triángulos
congruentes.
A
P
B
O
α°
α°
APO BPO
PA = PB
AO = OB
Teorema de la mediatriz. Cualquier punto perteneciente a la mediatriz asociada a un
segmento equidista de los extremos de dicho segmento; determinando así dos triángulos
rectángulos congruentes.
PH: mediatriz de AB
APH BPH
PA = PB
m PAH = m PBH
Teorema de la mediana relativa a la hipotenusa. La mediana trazada hacia la hipotenusa
de un triángulo rectángulo mide la mitad de dicha hipotenusa.
BE = AC
2
Teorema de la base media y de los puntos medios. En todo triángulo el segmento que
une los puntos medios de dos lados mide la mitad del tercer lado, y al mismo tiempo es
paralelo a dicho lado.
E F
B
A C
EF: base media
EF = AC
2
Además: EF // AC
P
A B
H
B
A C
E
Observa
Se debe trazar una
perpendicular desde
P al lado OB
Se recomienda
trazar una paralela
que pase por M y se
vuelva base media.
Si AM = MC = BM
Se debe trazar PB
m B = 90°
A
P
B
O
α°
α°
P
A B
M
B
B
A C
A
M
C
M
Sugerencia de trazo
¿Sabías que...?

56
Recuerda
Los criterios básicos
para identificar la
congruencia son:
• Lado - Ángulo - Lado
(L - A - L)
• Ángulo - Lado - Ángulo
(A - L - A)
• Lado - Lado - Lado
(L - L - L)
Calcula el valor de x, si AB = BC y BD = BE.
B
A
D
30°
x
E
C
Resolución: A partir de los datos se tiene:
Se nota: DBA EBC (L – A – L)
Por lo tanto: x = 30°
Los triángulos:
CRA DCE
∴ CE = RA = 5 u
AC = DE = 8 u
AE = 13 u
Como ARC es isósceles
AR = RC
∴ ARD RCE
Finalmente: x = 4 u
Halla el valor de AE, si RC = CD.
Resolución:
Resolución:
4 u
θ°
θ°
α° α°
D
A
C
E
R
x
Nota
a
b
R
E
triángulos
congruentes
b
α°
a
Rpta. 30°
Rpta. 13 u
Rpta. 4 u
B
A
D
30°
x
E
C
5 u
8 u
C
R
A
D
E
5 u
8 u
C
R
A
D
E
8 u 5 u
4
D
A C
E
R x
1
2
3
α°

57
4
5
6
Recuerda
Recuerda
Se sugiere trazar la
mediana BM:
Se cumple:
En la figura mostrada, determina el valor de x, si AR = 10 cm.
• Al trazar la mediana RM, RMD es
isósceles m RMA = 2α
• ARM: isósceles ∴ RM = 10 cm
Pero: RM =
QD
2
QD = 20 cm
• Dato: AR = DC.
• RDE es isósceles RD = DE
• m RDC = m ARD + m RAD
∴ m ARD = m EDC = b
Por teoría ARD CDE (LAL).
Se sabe que: PT = x – 3.
MN: base media del OPT
MN =
PT
2
5 =
x – 3
2
13 cm = x
A C
B
2k
Resolución:
En la figura se cumple que AR = DC. Calcula el valor de x.
Resolución:
50°
50°
x
R
C
D
A
E
En la figura mostrada, halla el valor de x, si se sabe que OM = MP.
Resolución:
A
P
R
5 cm
M
O
x – 3
A
Q
D
x
R
2α α
x = 50°
50°
50°
x
R
C
D
A
E
b
b
A
P
R
5 cm
M
N T
O
x – 3
A K K
M
K
C
2k
B
b° α°
α°
b°
* ABM y CBM
son isósceles.
2k
k
a = b
BM =
AC
2
m
m
α°
α°
A Q M
D
1
0
R
2α° 2α°
α°
α°
Rpta. 20 cm
Rpta. 50°
Rpta. 13 cm

58
k
Recuerda
Recuerda
Si L es mediatriz de
AB, entonces:
L AB, también
AM = MB
Si LM es mediatriz,
se recomienda
trazar
LB ya que:
LA = LB
Encuentra el valor de x en la siguiente figura, si L es mediatriz de AC.
Resolución:
En la figura mostrada, determina el valor de x.
Resolución:
A C
3b
L
9 u 3x
B
10 u
8x
B
N
M
C
A
10 u
B
Q
N
R
M
P
C
A
8x
2k
• MN: base media del PQR
• PQ: base media del ABC
• Por teoría:
MN =
PQ
2
PQ = 20 u
• También:
PQ =
AC
2
20 =
8x
2
∴ 5 u = x
• m B = 2 (ángulo exterior)
• Como L es mediatriz:
APC: isósceles AP = PC = 9 u
m ACP = β ∴ m CPB = 2β
• Se nota: PBC: isósceles
9 = 3x x = 3 u
L
B
M
A
MN: base media

Rpta. 3 u

Rpta. 5 u
L
B
M
A
Sugerencia
7
8
3x
A C
3b
L
P
9 u
β β
B
2β
2β
9 u

59
Síntesis
Modela y resuelve
Criterios • L – A – L : Lado – Ángulo – Lado
• A – L – A : Ángulo – Lado – Ángulo
• L – L – L : Lado – Lado – Lado
Aplicaciones
Teorema de la bisectriz Teorema de la mediatriz
Teorema de los puntos medios Teorema de la mediana relativa a la hipotenusa
m
m
a
a
P
B
A
L
A C
M N
B
⇒ MN // AC
⇒ PA = PB
B
A M C
2k
k k
k
BM =
AC
2
También MN =
Si AM = MB
∧ BN = NC
Sea L: mediatriz
de AB
AC
2
a
a
2 Determina, en cada caso, si los triángulos son
congruentes o no. Si la respuesta es afirmativa
escribe el caso que lo sustenta:
1 Determina, en cada caso, si los triángulos son
escribe el caso que lo sustenta:
a)
b)
50°
F
G
E
a)
b)
E
10 cm 10 cm
8 cm 8 cm
F
7 cm 7 cm
D P
Q
R
A
80°
70°
R
Q
70°
6 u C
P
6 u
30°
50°
I
H J
40°
60°
M
N
P
T
80°
40°
Q
R
Rpta.
Rpta.
Rpta.
Rpta.

60
Halla el valor de x, si BH es mediatriz de AC.
Halla el valor de x
2
.
Encuentra el valor de b – a.
Determina el valor de AD, si BC = CE, AB = 10 cm
y ED = 12 cm.
50° 30°
x
3 u
a
b
7 u
65°
95°
65°
x
20°
8 cm
8 cm
2x
42°
B E
A
C
D
a a
a
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
150°
x
4x
20 cm 16 cm
a
b
b
a
4 cm
3 cm
B
H C
A
x
3 4
5 6
7 8
9 10

61
12
11
14
13
16
15
18
17
Calcula el valor de CE, si AC = DE, BC // DE;
AB = 8 u y BC = 10 u.
Si XN = MZ y TN = TZ. Calcula el valor de θ, si
m XTN = 20°.
Resolución:
Resolución:
Encuentra la longitud del segmento MN, si
AB = 16 u, BC = 18 u y AC = 20 u.
Encuentra el valor de BC, si PQ = 2 u.
Resolución:
Determina el valor de x, si AC = CD. Determina el valor de x, si OM = MP.
Resolución:
Resolución:
Halla el valor de x. Halla el valor de m, si m + n = 24 cm.
Resolución:
Resolución:
Resolución:
x – 6
5 cm
R
C D
E
A
A
3 + 2x
P
15 cm
a
o B
a
T
40° 140°
M
N
X
θ
Z
m
n
M
C
A
Q
B
P
2x + 8
3x
M
A
O
P
θ
θ
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
B
N
C
A
a
θ
θ
a
M
B
A
D
E
C
a a

62
Halla el valor de x, si MN es mediatriz de AC .
Calcula el valor de AC.
Encuentra el valor de DC, si AB = BC; AE = 6 y
DE = 9.
Determina el valor de m PBQ, si m ABC = 110°.
Halla el valor de AC + DE, si AB = BE; BC = 7 cm;
CD = 2 cm.
Encuentra el valor de DE, si AB = BC; AE = 9 u
y DC = 21 u.
Se tiene un triángulo ABC, cuya medida del ángulo
B es 120°; se trazan las mediatrices de los lados
AB y BC; las cuales intersecan al lado AC en P
y Q, respectivamente. Determina el valor del ángulo
PBQ.
Resolución:
Resolución:
Resolución:
Resolución:
Resolución:
Resolución:
Resolución:
Resolución:
M
2x – 1
36°
N
A
72°
x
+
5
B
C
A
D
B E
C
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
20
22
24
26
19
21
23
25
E
D
f
f
C
B
A
x
6 cm
11 cm
4 cm
A
B
C
5 cm
q
q
A E
D
B
C
A E
D
B
C
A
P
B
Q
C

63
Nivel I
Determina, en cada caso, si los triángulos son
escribe el caso que lo sustenta.
Halla, en cada caso, si los triángulos son
escribe el caso que lo sustenta.
39
74°
69°
37°
25
40
40
25
x
39
a
a
a
R
Q P
12
8
M
N
8
12
A
M
R
N
16
a
θ
F
G
18
H
a
θ
b
b
a
a
II
I
A 37°
B 74°
C 69°
D 111°
E 90°
1
4
5
6
2
3
Determina el valor de 3x.
2
x
‒
3
5 cm
5 cm
1
7
c
m
a
a
b
b
2x2 – 4
4 cm
θ
θ
A 110°
B 200°
C 100°
D 130°
E 120°
A 21 cm
B 12 cm
C 17 cm
D 14 cm
E 30 cm
A 2 cm
B 4 cm
C 6 cm
D 8 cm
E 10 cm
130°
x

64
Encuentra el valor de OH, si AB = 16 cm; AM = MC
y BO = OM.
Encuentra el valor de a + b.
Determina la longitud de x.
4 cm
a
b
6 cm
a
a
25 m
24 m
x
x + 1
3x – 3
A 15 mm
B 10 mm
C 21 mm
D 3 mm
E 6 mm
A 1 u
B 2 u
C 3 u
D 4 u
E 5 u
A 12 cm
B 8 cm
C 4 cm
D 2 cm
E 6 cm
A 2 cm
B 4 cm
C 6 cm
D 8 cm
E 10 cm
A 4,5 cm
B 9 cm
C 12 cm
D 16 cm
E 18 cm
A 104 m
B 37 m
C 23 m
D 7 m
E 13 m
x 9 cm
φ
φ
b
b
Nivel II
7
8
9
10
11
12
D
10 mm
E
C
R
x
A
θ
θ
B
H
O
A M C
53°

65
13 16
14 17
15 18
Determina el valor de θ. Encuentra el valor de DE, si AB = BC; AE = 12 u
y DC = 23 u.
Halla el valor de x. Determina el valor de a + θ, si AM = MB y AN = NC.
Halla el valor de x, si AB = BC y BD = BE.
B
9 u
C
D
A
a
a
θ
θ
x2
A
6
B
C
D
x2 + 2
E
D
30°
C
B
E
A
θ
A 20°
B 40°
C 80°
D 60°
E 50°
A 9 u
B 13 u
C 12 u
D 10 u
E 11 u
A 90°
B 75°
C 120°
D 180°
E 135°
A 80°
B 70°
C 100°
D 90°
E 30°
A 1 cm
B 2 cm
C 3 cm
D 6 cm
E 5 cm
A 9 u
B 4,5 u
C 3 u
D 2 u
E 1 u
B
A E
C
D
B
E
D
A C
30°
x
a
a
100°
B
M
A
H N
C
θ
a

66
Encuentra el valor de x, si OM = MP.
Encuentra la medida de PQ, si BC = 10 cm;
HC = 3 cm.
Determina la m PBQ, si m ABC = 100°.
Halla el valor de MN, si MN // AD; AD = 6 cm y
AM = MB.
En la figura mostrada, calcula el valor de x.
Calcula el valor de x, si AB = 10 cm.
B
C
A
P Q
A 10 cm
B 18 cm
C 15 cm
D 20 cm
E 25 cm
A 4 u B 5 u C 8 u
D 6 u E
7 u
D 5 cm E
Faltan datos
A 11 cm
B 8 cm
C 12 cm
D 7 cm
E 13 cm
A 10° B 20° C 15°
D 25° E
30°
D 6 cm E
5 cm
B
P Q
A C
H
a
a
A
2x – 8
P
R
9 cm
M
O
a
a
B
N
M
A C
D
D
B
3x
M
x + 8
Q
P
A C
22
19
23
20
24
21
Nivel III
B
2a
x
A D
P
a

Test n.° 2
67
En la figura, encuentra el valor de BC, siAB = 5 cm. Halla el valor de x.
Calcula el valor de x. Encuentra la longitud de x, si AP = PC.
Según el gráfico, determina el valor de x. El ABC es equilátero, calcula el valor de x.
1 4
2 5
3 6
3 cm
A
10 cm
C
6 cm
B
12 cm
D
6 cm
A
8 cm
C
4 cm
B
3 cm
D
8 m
A
5 m
C
6 m
B
3 m
D
5 u
A
10 u
C
6 u
B
7 u
D
2 mm
A
4 2 mm
C
2 2 mm
B
8 2 mm
D
10 m
A
10 2 m
C
5 m
B
6 m
D
B
A C
30°
37°
16 cm
B
H
A C
15°
x
45°
8 mm
x
B
A C
37°
60°
x 5 3 m
B
E
A C
P
37°
20 m
x
4 u
x
A C
B
3 3 u

68
Determina el valor de x. Calcula el valor de CF, si ABCD es un cuadrado;
EF = 19 cm y AE = 8 cm.
Halla el valor de AE, si BC = CD. En la figura mostrada, determina el valor de x.
Encuentra el valor de a – b. Halla la longitud del segmento MN, si AB = 12 u,
BC = 16 u y AC = 20 u.
7 10
8 11
9 12
20 m
A
15 m
C
22 m
B
25 m
D
23 u
A
13 u
C
10 u
B
14 u
D
1 u
A
3 u
C
2 u
B
4 u
D
12 cm
A
13 cm
C
10 cm
B
11 cm
D
2 cm
A
4 cm
C
3 cm
B
5 cm
D
20 u
A
24 u
C
22 u
B
10 u
D
7 m
x
24 m
B
A C E
D
5 u 8 u
b
a
3 cm
8 cm
a
a
A
E
D
B
C
F
B
2x – 2
M
x + 2
Q
P
A C
A
B
M
N
C
a q q
a

Tema
69
5
Cuadriláteros I
La imagen muestra campos de siembra de tulipanes en Holanda, con su habitual
disposición en forma de cuadriláteros diversos. Tienen distintos colores debido a los tipos
de esta hermosa flor.
Generalidades sobre los cuadriláteros
• Polígono de 4 lados.
• La suma de las medidas de los ángulos interiores es 360º.
• Tiene dos diagonales.
Clasificación
La clasificación de los cuadriláteros se da en función al paralelismo, debido a ello tiene:
• Trapezoides: Ningún par de lados son paralelos.
• Trapecios: Un par de lados son paralelos.
• Paralelogramos: Dos pares de lados son paralelos.
Observación
Cuadrilátero no convexo o cóncavo. Es aquel cuadrilátero con una región interior no
convexa.
En los cuadriláteros convexos, las diagonales siempre serán interiores, ya que su
región interior es convexa. Por el contrario, en los cuadriláteros no convexos, una
diagonal es externa debido al tipo de región interior.
Convexo No convexo
Cuadriláteros
Notación
ABCD: Cuadrilátero ABCD
Diagonales: AC y BD
α° + β° + φ° + ω° = 360°
B C
A D
Notación
ABCD: Cuadrilátero no convexo
Diagonales: AD y BC
α° + β° + φ° + ω° = 360°
A D
B
C
β°
β°
α°
α° ω°
ω°
φ°
φ°
Observa
La palabra
cuadrilátero proviene
del latin:
quatuor: cuatro
latus o lateris: lado
¿Se dice no
convexo o
cóncavo?
Aunque los dos
son admitidos,
es más usual
utilizar cóncavo en
superficies curvas.
Por ejemplo: una
antena parabólica.
Por ello, en
polígonos se
recomienda utilizar
la expresión no
convexo.
En un polígono se
denomina diagonal
a un segmento que
une dos vértices no
consecutivos.
¿Sabías que...?
¿Sabías que...?

70
a = b
a = b a = b
a = b
a = b
Observa
También se cumple:
Relaciones angulares en los cuadriláteros:
x =
α° + β°
2
Clasificación de cuadriláteros de acuerdo al criterio del paralelismo
Trapezoides: Cuadrilátero en el cual ningún lado es paralelo a otro.
Un tipo especial de trapezoide es el trapezoide simétrico también llamado trapezoide
bisósceles. Su principal característica es que una diagonal es mediatriz de la otra, siendo
así eje de simetría del polígono, esto último determina una observación implícita: las
diagonales son perpendiculares entre sí.
De acuerdo a esto se generan dos triángulos isósceles, de allí su nombre.
x =
α° – β°
2
x =
α° – β°
2
Por simetría también tendríamos:
m BAM = m DAM
m BCM = m DCM
x
b°
a°
x =
x =
a° + b°
2
a° + b°
2
a°
α°α° β°
β°
x
b°
B
C
A D
x
β°
θ° θ°
ω°
ω°
α°
B
C
D
A
x
α°
ω°
q° q°
ω° β°
α° β°
β°
α°
B
M
A C
D
Sea AC mediatriz
de BD, entonces:
AB = AD
BC = CD
También
α°
α°
β°
β°
B
D
C
x
A
ω°
ω°
α°
θ°
θ°
β°

71
a = b
a = b
Trapecios: Cuadriláteros donde dos lados son paralelos, estos lados son llamados
bases, y la separación entre ellos será la altura del trapecio. Los ángulos adyacentes
a cada lado no paralelo son suplementarios. Se clasifican en:
• Trapecio escaleno: Sus lados no paralelos son desiguales.
• Trapecio recto o trapecio rectángulo: Uno de los lados no paralelos es
perpendicular a las bases. Dicho lado mide igual a la altura.
• Trapecio isósceles: Sus lados no paralelos son congruentes.
En todo trapecio isósceles se cumplen las siguientes características:
1. Lados no paralelos congruentes: AB CD
2. Diagonales congruentes: AC BD
3. Ángulos formados por las bases:m BAD = m CDA
También: m ABC = m BCD
Teoremas que cumplen todos los trapecios
Suma de las medidas de los ángulos adyacentes a un lado no paralelo. Estos ángulos
siempre son suplementarios, y esto se da por el paralelismo que hay entre las bases.
° + ° = 180°
Longitud de la mediana (base media) del trapecio. En todo trapecio la mediana o base
media mide igual a la semisuma de las longitudes de las bases. También se cumple que
esta es paralela a ellas.
MN =
B + b
2
También:
MN // QR // PS
B
A D
C
β°
α°
B
b
Q R
M N
P S
β°
β° α°
α°
Base
Base 2
b m n
a Altura
β°
α°
α° + β° = 180°
A D
C
B
α° α°
a
a
β° β°
Es un trapecio
isósceles.
A la base media de
un trapecio también
se le llama mediana.
Si el trapecio
ABCD está inscrito,
entonces es un
trapecio isósceles.
Base
menor
Base
mayor
Observa
Observa
α°
α°
¿Sabías que...?
B
A
C
D

72
Observación: La mediana o base media de un trapecio biseca a las diagonales.
• Sea MN: base media
del trapecio.
MN PR = {W}
⇒ PW = WR
Longitud del segmento que une los puntos medios de las diagonales. Este segmento
mide la semidiferencia de las longitudes de las bases.
Observación: MN está contenido en la mediana del trapecio, por lo tanto: MN//QR// PS.
Si MN // QR // PS
⇒ x =
Bk + bm
m + k
b) En un trapecio las bases intermedias equidistantes forman una progresión aritmética.
a) En todo trapecio se cumple que:
• PR y QS: diagonales
⇒ MN = B – b
2
M y N: puntos medios
de las diagonales
Otras propiedades importantes
Q R
M N
S
W
P
b
B
Q
P S
M N
R
b
B
M
k
m
R
N
Q
P
x
S
b
B
x
x + r
x + 2r
x + 3r
x + 4r
n
n
n
n
m
m
m
m
Observa
Reflexiona
Reflexiona
¿En un trapecio
puede la altura
medir igual a un
lado no paralelo?
¿En un trapecio
una diagonal puede
medir igual a la
altura?
P Q
PQ: base media del
trapecio.

73
No olvides
En todo trapecio
a, b, c, d y e forman
una progresión
aritmética.
m°
En la figura se muestra un trapecio. Halla el valor de x. x =
m° + n°
2
Resolución:
Por teorema:
x =
100° + 98°
2
x = 99°
Resolución:
Los ángulos mostrados son
suplementarios:
13x + 5x = 180°
x = 10°
B C
13x
A D
5x
En la figura se muestra un trapecio, encuentra el valor de x.
Resolución:
El segmento mostrado es el llamado «segmento que une los puntos medios de las
diagonales», cuya medida es la semidiferencia de las longitudes de las bases, por
lo tanto:
x =
17 – (x + 5)
2
x = 4 cm
Las bases y la mediana de un trapecio suman 6 m. Determina la longitud de su
mediana.
Resolución:
Debemos recordar que todas las bases equidistantes de un trapecio forman una
progresión aritmética:
x – r
x
x + r
Q
M
P S
N
R
Por lo tanto, tendríamos según el dato:
(x – r) + (x) + (x + r) = 6 m
x = 2 m
β°
β°
α°
α°
n°
x
a°
x =
a° – b°
2
β°
β°
α°
α°
b°
x
a
b
c
d
e

Rpta. 99°

Rpta. 10°

Rpta. 4 cm

Rpta. 2 m
100°
98°
x
α°
α° θ° θ°
P Q
x
17 cm
x + 5
1
2
3
4

74
La base mayor de un trapecio rectángulo mide 30 cm, su altura 10 cm y el ángulo
agudo de la base 45°. La mediana mide:
Resolución:
En un cuadrilátero convexo ABCD, m A = 60º, m C = 110º. Halla la medida del
menor ángulo formado por las bisectrices interiores de los ángulos B y D.
En un trapecio isósceles de 20 cm de perímetro y de bases 2 cm y 8 cm, calcula la
medida del menor ángulo interno.
Resolución:
Resolución:
Por teorema:
x =
110° – 60°
2
x = 25°
D
C
B A
x
110°
60°
30 cm
10 cm
B C
M
A
D
10 cm
10 cm
20 cm
20 cm
45°
45°
AB = CM = 10 cm
DM = 10 cm
∴ AM = 20 = BC
∴ Mediana =
BC + AD
2
Mediana =
20 + 30
2
= 25 cm
Como el perímetro es 20 cm
2 + 8 + 2a = 20 cm
a = 5 cm
CDH
C
H
5 cm
3 cm
x
D
⇒ x = 53°
a
B C
A D
2 cm
2 cm
3 cm
3 cm
8 cm
a
=
5
cm
x
H
Graficando:

Rpta. 25°

Rpta. 53°

Rpta. 25 cm
No olvides
No olvides
k 2
k
k
45°
45°
5k
4k
3k
53°
37°
k
2k
30°
60°
k 3
m°
x =
m° – n°
2
β°
β°
α°
α°
n°
x
5
6
7

75
Síntesis
Modela y resuelve
Los cuadriláteros son figuras de cuatro lados. Características
Trapezoide. Se caracteriza porque ninguno de sus lados es paralelo a otro.
Trapecio. Presenta un par de lados paralelos llamados bases.
x = x = x =
m° + n°
2
m° – n°
2
m° – n°
2
x
n°
m° n°
n°
m°
m°
x
a
a
a
a a
a
b b b b
b
b
x
B C
M N
A D
MN: Base media o mediana del trapecio.
MN =
BC + AD
2
A D
E F
B C
E: Punto medio de AC
F: Punto medio de BD
EF = AD – BC
2
– Presentan dos diagonales.
– La suma de sus ángulos internos es 360°.
Según la figura, calcula el valor de x.
Según el gráfico, calcula el valor de x.
B
A D
C
140°
2b
b
E
x
70°
2φ
φ
B
150°
2φ
φ
x
E
2α
30°
C
D
A
a
1 2
Rpta.
Rpta.
Cuadriláteros I

76
Grafica el cuadrilátero ABCD, tal que m A = 100°;
m B = 70° y m C = 60°. Encuentra la medida
del ángulo CDA.
Grafica el trapezoide ABCD, tal que m A = 2b°;
m B = 5b°; m C = 7b° y m D = 4b°. Encuentra
la medida del ángulo ABC.
Grafica el trapecio isósceles ABCD, tal que
m A = 118°. Determina la medida del ángulo
BCD.
Grafica el cuadrilátero PQRS, tal que m P = 68°;
m Q = 136° y m R = 120°. Determina la medida
del ángulo RSP.
Según el gráfico, halla el valor de x.
Resolución:
Resolución:
B
100°
E
x
A
C
D
4x
3x
2x
x
Resolución:
Resolución:
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
4
6
8
3
5
7

77
En el trapecio ABCD (BC // AD), AP = 2(BP),
QD = 2(CQ), PQ = 6 cm y AD = 10 cm. Calcula el
valor de BC.
En el trapecio ABCD (BC // AD), AB = 12 m,
BC = 10 m, CD = 8 m. Calcula la longitud de la
base media del trapecio.
B C
P Q
A D E
A D
B C
a
a θ
θ
9
11
13
10
12
14
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Si el segmento que une los puntos medios de
las diagonales de un trapecio mide 6 u y la base
menor de dicho cuadrilátero 18 u, halla la medida
de la base mayor.
Los ángulos de un cuadrilátero son 5x, 3x, 4x y
6x. Halla el valor del ángulo mayor.
Resolución:
Resolución:
Determina la medida de x. ABCD es un trapecio, donde: CD = 4 2 cm.
Determina el segmento que une los puntos
medios de las diagonales.
x
θ
θ
a
a
60°
40°
B
A
C
D
40°
70°

78
En un trapecio la mediana y el segmento que
une los puntos medios de las diagonales suman
13 cm. ¿Cuál será la medida de su base mayor?
En un trapezoide ABCD, m A = 90°, AB = AD
y BC = CD. Si m ABC = 105°. Encuentra la
m BCD.
Resolución:
Calcula el valor de x. Calcula el complemento de x.
Resolución:
Resolución:
Resolución:
20°
x
60°
40°
4x
3x
2x
Se tiene un cuadrilátero ABCD donde:
m B = m D = 90°. Halla la medida del ángulo
exterior de C, si m BAD = 40°.
En el trapecio isósceles ABCD, halla el valor de α.
Resolución:
Resolución:
3α
2α
A D
C
B
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
16
18
20
15
17
19

79
En el trapecio ABCD (BC // AD), AB = 6 u, BC = 4 u,
CD = 8 u, AD = 16 u, BM = ME, CN = NF. Calcula
el valor de MN.
En la figura, AB = BC = 8 cm, encuentra la longitud
del segmento que tiene por extremos los puntos
medios de las diagonales.
b
b
θ
θ
M N
A
B C
E F
D
En el trapecio ABCD (BC // AD), AB = 6 cm,
BC = 4 cm, CD = 8 cm. Halla la longitud de la base
media del trapecio.
b
b
a
a
B C
A
E
D
En el trapecio ABCD, BC = 3 cm, PQ = 5 cm,
AP = 2PB, QD = 2CQ. Determina el valor de AD.
B C
P Q
A D
B C
A D
53°
En el trapecio isóscelesABCD (BC //AD),AB = 10 m.
Calcula la longitud del segmento que tiene por
extremos los puntos medios de las diagonales.
60°
B
A
C
D
A 3 u B 4 u C 2 u
D 5 u E
1 u
D 1 cm E
2,5 cm
A 7 m B 6 m C 8 m
D 4 m E
5 m
D 7,5 cm E
11 cm
D 10 cm E
11 cm
Nivel I
1
2
5
3
6
4

A 125°
B 160°
C 135°
D 115°
E 130°
B
A D
C
120°
1
4
0
°
x
I

80
Si ABCD es un trapecio isósceles (BC // AD),
determina el valor de x.
2x + 10°
B C
A D
140°
Encuentra el valor de x, si m B – m D = 60º
Calcula los valores de α y θ, si BC // AD.
B C
A D
118°
2α 4θ
140°

A 75°
B 70°
C 60°
D 55°
E 65°

A 30°
B 140°
C 150°
D 130°
E 160°
A 26° y 30°
B 31° y 10°
C 45° y 45° D 62° y 40°
E 37° y 53°
x
A D
B
C
a
a
θ
θ
Grafica el cuadrilátero ABCD, tal que AD // BC,
m A = 100°; m D = 50°. Halla m B y
m C, respectivamente.
Grafica el cuadrilátero convexo ABCD, tal que
m A = m C = 90° y m B = 112°.
Determina la m D.
Traza el trapecio ABCD, tal que: m A = 120°;
m B = 130° y AB // CD. Indica, respectivamente,
las medidas de los ángulos ADC y BCD.
A 70° y 120°
B 60° y 120°
C 80° y 130° D 80° y 100°
E 60° y 130°

A 130°
B 50°
C 65°
D 68°
E 60°
A 60° y 70°
B 50° y 80°
C 45° y 60° D 60° y 50°
E 40° y 70°
7 10
8 11
9
12
Nivel II

81
13 16
14 17
15 18
De la figura, determina el valor de x.
La mediana de un trapecio que mide x + 6 cm, si
sus bases miden x – 4 y 2x + 10 cm. Encuentra la
longitud de dicha mediana.
De la figura, calcula el valor de x.
2x
120°
x
a
a
θ
θ
Halla el valor de α + θ, si la figura muestra un
trapecio isósceles (BC // AD).
La figura muestra un trapecio, ¿cuál es el valor
de x?
B C
A D
P
x
α
α
θ
θ
En el trapezoide mostrado, indica el valor de x.
a°
a°
b°
θ°
θ°
b°
x°
85°
n°
n°
B C
A D
a
θ
B
A D
C
3x
4x
2x
θ
ω
ω θ

A 10°
B 15°
C 20°
D 25°
E 30°

A 30°
B 60°
C 45°
D 130°
E 90°

A 95°
B 105°
C 85°
D 35°
E 45°

A 6 cm
B 12 cm
C 8 cm
D 16 cm
E 7 cm

A 15°
B 30°
C 45°
D 60°
E 75°

A 90°
B 180°
C 360°
D 120°
E 160°

82

A 3 cm
B 5 cm
C 6 cm
D 7 cm
E 8 cm
x
α°
α°
3 cm
En el trapecio mostrado calcula la longitud de su
mediana.
b
b + 3
11 m
El perímetro de un trapecio isósceles es
240 cm. Halla la medida de la mediana si el lado
no paralelo mide 50 cm.
Si el cuadrilátero ABCD es un cuadrado y CDE
es un triángulo equilátero, determina la m AEC.

A 7 m
B 8 m
C 9 m
D 10 m
E 5 m

A 35 cm
B 60 cm
C 50 cm
D 65 cm
E 70 cm

A 15°
B 30°
C 37°
D 45°
E 53°
En un trapecio ABCD (BC // AD), encuentra la
m BDA, si m ABC = 140°, AB = AD.
En el gráfico, calcula el valor de x, si a + b = 240°.
a
b
x
2a
θ
2θ
a

A 10°
B 20°
C 30°
D 40°
E 70°

A 20°
B 30°
C 40°
D 50°
E 60°
Nivel III
22
19
23
20
24
21
B C
E
A D

Tema
83
6
Cuadriláteros II
a = b
a = b
En la imagen se observa dos edificios, donde sus fachadas muestran dos regiones
paralelográmicas.
Paralelogramos
Son aquellos cuadriláteros con dos pares de lados opuestos congruentes y paralelos:
a° + b° = 180°
a° + q° = 180°
Como se puede ver en el gráfico los ángulos opuestos miden igual y los ángulos
adyacentes son suplementarios.
Dentro de este grupo de figuras encontramos 4 figuras geométricas que cumplen con
estas características, y son las siguientes:
El romboide: También llamado «Paralelogramo», es el más simple de los miembros
de esta familia. Básicamente, en él, se van a cumplir las propiedades principales de los
paralelogramos:
A
B C
b
b
a
q° a°
a° q°
a
D
A
B C
b
b
a a
a° b°
a°
b°
D
AB // CD
BC // AD
Si L1 y L2 son
paralelas
Ángulos
suplementarios: Son
dos ángulos cuya
suma es 180°.
Recuerda
b°
a°
L1
L2
a = b
a° + b° = 180°

84
Recuerda
Históricamente
Losange era así:
Polígono
equiángulo
Polígono
equilátero
Polígono
regular
El rombo: Antiguamente llamado Losange. Es un cuadrilátero equilátero. Además, sus
diagonales son perpendiculares y se bisecan mutuamente.
El rectángulo: También llamado Cuadrilongo. Es un paralelogramo equiángulo. Una de
sus principales características es que sus diagonales son congruentes.
El cuadrado: También llamado Cuadrilátero regular. Como su nombre lo indica, es un
polígono regular, es decir, sus lados miden igual, al igual que todos sus ángulos.
En el caso del cuadrado, además, nota que las diagonales son congruentes y
perpendiculares. También estas mismas diagonales son bisectrices de los ángulos rectos,
por lo tanto determinan ángulos de 45º.
1) ¿Cuánto miden los ángulos interiores de un cuadrado?
2) ¿Cuántas diagonales tiene un cuadrilátero?
3) ¿Cuánto suman los ángulos internos de un cuadrilátero?
4) ¿Cómo son las medidas de los ángulos opuestos de un paralelogramo?
5) ¿Cómo son las diagonales de un rectángulo?
6) ¿Cómo son las diagonales de un rombo?
Responde las siguientes interrogantes en tu cuaderno y luego discútelas en clase con tu
profesor:
Actividad en tu cuaderno
45° 45°
l
l
l
l
l
l
l
l
l
l
l
¿Sabías que...?
a
a
a
a
a
l
l
l
l
l
l
a
a
a
a
a
a
a
a
l l
l
l
B
45°
45°
45° 45°
45°
45°
A
C
D
n
n
n
n
45° 45°
O
l
l
A
B
D
a° a°
b°
b° b°
C
b
a
b
l
l
a
a° a°
B C
a a
b
b
O
A D
l
l l
l

85
Dibujemos un cuadrado usando regla y compás
Actividad en tu cuaderno
N
L
M
Primer paso
Traza un ángulo recto usando una escuadra
o cartabón, considerando que los lados de
tal ángulo recto sean mayores que el lado del
cuadrado que quieras dibujar.
Segundo paso
Coloca la punta del compás en el vértice del
ángulo recto dibujado en el paso previo, por
ejemplo, en el punto M, ajusta el ancho del
compás para que tenga igual al largo deseado
de los lados del cuadrado. Este ancho debe
permanecer intacto hasta que se haya
terminado de dibujar.
Tercer paso
Dibuja otro arco que intersecará el lado LM en
algún punto (el punto Q).
Cuarto paso
Coloca la punta del compás en el punto Q y
dibuja un arco en algún punto debajo del lado
MN.
Para hacer esta
actividad necesitas:
• Regla
• Escuadra
• Cartabón
• Lápiz
• Papel
• Compás

86
Quinto paso
Coloca la punta del compás en el punto
P y dibuja otro arco que intersecte al arco
dibujado en el paso previo en algún punto
(digamos el punto R).
Sexto paso
Conecta los puntos P y R y los puntos Q
y R usando una regla de borde recto.
¿Sabías que...?
Ahora hazlo tú:
Sétimo paso
La figura PMQR es un cuadrado. Puedes borrar las demás líneas innecesarias,
si así lo deseas.
M
Q
P
R
• Dibuja un cuadrado y traza todas sus diagonales.
• Grafica un cuadrado con perímetro de 16 cm (utiliza regla y escuadras).
Escuadra
Cartabón
45°
45°
60°
30°

87
Un triángulo
equilátero es un
polígono regular, por
lo tanto, sus lados y
también sus ángulos
interiores miden
igual.
Recuerda
D
A
B C
E
x
Incógnita: x
En el B: y + x = 90° ................................ (1)
SiABCD es un cuadrado yAED es un triángulo equilátero
⇒ AD = AE = AB = a
Luego en el ∆ isósceles ABE:
2y + 30° = 180° ⇒ y = 75° ......................... (2)
Reemplazando (1) en (2)
75° + x = 90° ∴ x = 15°
• Como: BC // AD
⇒ m BEA = b (alternos internos)
∆ ABE: isósceles
⇒ AE = 12 cm ∴ ED = 18 cm
• Piden base media MN = x
⇒ x =
30 + 18
2
= 24 cm
E
E
D
D
B
B
C
C
A
A
1 En la figura, ABCD es un cuadrado, AED es un triángulo equilátero. Calcula el valor
de x.
2 La figura ABCD es un romboide, BC = 30 cm, CD = 12 cm. Halla la longitud de la base
media del trapecio BEDC.
a a
A C
B
60°
60° 60°
a
Si BE es bisectriz
En un trapecio
Entonces
∆ ABE: isósceles
¿Sabías que...?
Resolución:
Resolución:
E
D
B C
A
b
b

Rpta. 15°

Rpta. 24 cm
α°
α°
α°
α°
α°
D
A
B C
E
60°
60°
60°
30°
x
y
a
a
a
a a
a
y
1
2
c
m
1
2
c
m
E
D
B
x
M N
C
A
b
b
18 cm
12 cm
30 cm
b

88
El rombo es
un cuadrilátero
equilátero. Por lo
tanto, sus lados
miden igual.
Recuerda
Observa
Observa
Propiedad:
En un trapecio.
Se recomienda como
trazo CE // AB: Se
forma un paralelogramo
ABCE.
2(m BAC) = m BOC
A
D
C
B
106°
70°
A
B C
D
40°
3 En la figura, ABCD es un rombo de perímetro igual a 60 m. Encuentra el valor
de AC.
4 En la figura, ABCD es un trapecio donde BC // AD, BC = 4 m, CD = 6 m. Determina el
valor de AD.
5 Calcula el valor de x, si la figura ABCD es un rombo (AD = BE).
A
B
C
D
E
5x
2x
15 m
15 m 15 m
A
D
C
B
O
106°
53° 53°
Si el perímetro es 60 m, cada lado mide 15 m.
• Como: BD es mediatriz de AC
⇒ m OBC = m OBA = 53°
• BOC: notable (37° y 53°)
⇒ OC = 12 m ∴ AC = 2(OC) = 24 m
• Trazo sugerido CF // AB
⇒ m BAD = m CFD = 70°
⇒ BC = AF = 4 m
• CFD: Al completar ángulos internos
notamos que es isósceles.
⇒ FD = CD = 6 m
∴ AD = 4 m + 6 m = 10 m
• Se nota: AB = BC = BE
• Por propiedad m EAC = x.
• Como m AED = 5x:
ángulo exterior del ACE
⇒ m ACE = 4x.;
⇒ CA es bisectriz del BCD
∴ m BCD = 8x
• BCE: 18x = 180° ⇒ x = 10°
B
A E
C
D
4 m
4 m
6
m
B
A F
C
D
40°
70°
70° 70°
A x
O
C
B
2x
A
B
C
D
E
5x
x
2x
4x
4x
Resolución:
Resolución:
Resolución:

Rpta. 10 m

Rpta. 24 m

Rpta. 10°

89

Rpta. 50°

Rpta. 16°

Rpta. 100°
No olvides
Recuerda
Si L1 // L2
° = °
Alternos internos
q° + ° = 180°
Conjugados internos
Rectángulo
AC = BD
También:
AP = P C = BP = PD
B
20°
x
E
C
D
A
A
B
E
D
60°
3q
q
x
C
6 La figura ABCD es un rectángulo. Halla el valor de x.
7 En la figura, ABCD es un rectángulo, BC = 4k, CD = 3k. Encuentra el valor de x.
8 Si la figura ABCD es un rombo, determina el valor de x.
• BO = CO ⇒ BCO es isósceles
• m COD = 40°
• COE: x + 40° = 90°
x = 50°
• BC = AD = 4k
• CD = AB = 3k
• BAC: notable 37° y 53°
• m BDA = m CAD = 37°
• AED: x + 2(37°) = 90°
x = 16°
• m CDF = 4q: (alternos internos)
• 4q = 60° + q (ángulo exterior)
20° = q
• AB // CD: rombo
⇒ x y 4q son conjugados internos
x + 4(20) = 180° ⇒ x = 100°
20°
x
E
D
C
A
B
20°
40°
O
A
B
E
D
F
60°
3q
4q
q
x
C
B
A
C
P
D
L1
L2
q°
°
°
L1
L2
°
°
°
Resolución:
Resolución:
Resolución:
A
x
B C
D
E
A
x
B C
D
E
4k
4k
3k 3k
37°
37°

90
Síntesis
Modela y resuelve
1
Paralelogramos: Son cuadriláteros con dos pares de lados paralelos.
En todo paralelogramo se cumple:
Clasificación:
• Romboide
• Rectángulo
• Rombo
• Cuadrado
• AB = CD y BC = AD
• m A + m B = 180°
• BO = OD y AO = OC
• AC = BD
• AO = OC = BO = OD
• AC = BD
• BO = OD
• AO = OC
• m AOD = 90°
A D
O
C
B
A
B
D
O
C
A
B
D
O
45° 45°
45° 45°
C
L
L
L
L
a° a°
a° a°
θ°
θ°
θ°
θ°
De la figura, calcula el valor de x si ABCD es un
cuadrado.
En el romboide ABCD, calcula el valor de x.
12x
8x
B
B
C
C
D
D
A
A
x 30°
Resolución:
Resolución:
2
Rpta.
Rpta.
Cuadriláteros II

91
Grafica el rombo ABCD, tal que AB = 4 cm y
m A = 40° (utiliza regla y transportador). Indica
su perímetro.
Grafica el romboide ABCD, tal que AB = 3,5 cm y
BC = 5 cm. Indica el perímetro.
El perímetro de un paralelogramo mide 70 cm, el
lado mayor excede al lado menor en 3 cm. Halla la
medida del lado mayor.
Resolución:
Resolución:
Resolución:
Grafica el rectángulo PQRS, tal que PQ = 3 cm
y PS = 7 cm. Halla su perímetro y utiliza regla y
transportador.
Resolución:
Grafica un rombo ABCD, tal que BC = 5 cm y
m C = 120°. Luego, traza las diagonales AC y
BD. Mide el ángulo que forman sus diagonales
(utiliza regla y transportador).
Resolución:
Grafica un romboide ABCD, tal que CD = 4 cm,
AD = 8 cm y m D = 140°. Traza sus diagonales
y compara sus medidas (utiliza regla y
tansportador).
Resolución:
Siendo ABCD un rectángulo. Determina el valor de x. Determina el valor de x, si ABCD es un cuadrado
y AED es un triángulo equilátero.
Resolución:
Resolución:
B
A
C
D
x
E
B C
A D
x
62°
3
5
7
9
4
6
8
10
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.

92
Grafica el romboide ABCD, tal que AB = 3 cm,
BC = 5 cm y m B = 60° (utiliza regla y
transportador). Encuentra su perímetro.
Grafica el rombo ABCD, tal que AB = 4 cm y
m A = 40° (utiliza regla y transportador).
Encuentra su perímetro.
CalculaelvalordeBP,siABCDesunparalelogramo.
Resolución:
Resolución:
θ
θ
7 u
B
A
12 u
P
C
D
Halla el valor de a + b, si ABCD es un rombo.
Resolución:
5β
B
A C
D
2α + 30° 50°
74°
x
Si ABCD es un paralelogramo. Calcula el valor de
EF, si CE es bisectriz.
Resolución:
8 cm
3θ
θ
F
E
A
6 cm
C
D
B
En el gráfico, ABCD es un romboide, si CD = 10
cm, AP = PE, BQ = QD. Determina el valor de PQ.
En la figura, ABCD es un romboide, si BC = 10 cm,
CD = 6 cm, BM = MA, CN = NE. Determina el
valor de MN.
Resolución:
Resolución:
B
E
C
P Q
A D
θ
θ
B
M
A
E
D
N
C
b
b
Rpta.
Rpta.
12
14
16
18
11
13
15
17
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.

93
Nivel I
1
4
2
5
3 6
En la figura, ABCD es un rectángulo, tal que
AM = ME, CN = ND, AD = 8 y CD = 4 cm.
Encuentra el valor de MN.
B
A
45°
M N
D
C
E
¿Cuál es el ángulo que forman las diagonales de
un rombo?
Enlafigura,ABCDesunrectángulo,talqueBC=4k
y CD = 3k. Determina el valor de x.
E
x
B
A
C
D

A 16°
B 37°
C 56°
D 53°
E 45°

A 6 cm
B 5 cm
C 8 cm
D 4 cm
E 3 cm
¿Cuánto es la diferencia de las medidas de las
diagonales de un cuadrilongo?
A No conozco esa figura
B Faltan datos
C Depende de los ángulos
D 0
E Hay una diagonal mayor y una menor

A 20 cm
B 20 2 cm C 5 cm
D 10 cm
E 10 2 cm
A 19 cm y 140°
B 9,5 cm y 40°
C 19,5 cm y 140°
D 19 cm y 40°
E 9,5 cm y 140°
D
C
A
B
Si ABCD es un cuadrado, BD es la diagonal que
mide 5 2 , halla su perímetro.
A
B
D
C
5 2
Grafica el romboide ABCD, tal que AB = 3,5 cm,
BC = 6 cm y m B = 40°. Calcula su perímetro y
la medida del ángulo D.
A Faltan datos
B Se deben conocer solo los datos
C 90°
D 60°
E 180°

94
En la figura, ABCD es un paralelogramo, tal que
AB = 9 u y EF = 2 u. Encuentra el valor de AD.
En la figura, ABCD es un rectángulo, tal que
ED = 8 cm y FE = 12 cm. Determina el valor de
EC.
B
A
F
E
D
C

A 3 cm
B 6 cm
C 4 cm
D 5 cm
E 10 cm
En la figura, ABCD es un cuadrado y AED es un
triángulo equilátero, tal que AB = 8 2 cm. Calcula
el valor de DF.
F
B C
A D

A 6 cm
B 5 cm
C 8 cm
D 4 2 cm
E 3 2 cm
En la figura, ABCD es un cuadrado y CDE es un
triángulo equilátero. Halla el valor de x.
x
B
A D
C
E

A 45°
B 60°
C 30°
D 37°
E 74°
B
E F
C
D
A
a
a
θ
θ

A 19 u
B 16 u
C 18 u
D 22 u
E 20 u
Si las diagonales del rombo miden 14 cm y
48 cm, halla el perímetro del rombo.
En un rectángulo ABCD, se traza la bisectriz
BE (E en AD). Calcula la longitud de BC, si
AE = 3 cm y CE = 5 cm.

A 6 cm
B 7 cm
C 8 cm
D 9 cm
E 10 cm
B
A C
D

A 130 cm
B 140 cm
C 120 cm
D 150 cm
E 100 cm
Nivel II
7
8
9
10
11
12
E

95
13 16
14 17
15 18
Determina V o F de acuerdo a:
I. Un cuadrilátero de diagonales congruentes es
solo el rectángulo.
II.
El único cuadrilátero de diagonales
perpendicualres es el rombo.
III. Un cuadrilátero de lados congruentes solo es
el cuadrado.

A FFF
B FFV
C FVV
D VVV
E VFF
En un romboide ABCD, AB = 6 cm y BC = 14 cm.
Las bisectrices interiores de B y C intersecan a
AD en los puntos P y Q, respectivamente. ¿Cuál
es la medida del segmento que une los puntos
medios de BP y CQ?
En la figura, ABCD es un paralelogramo, donde
AB = 8 cm; BC = 13 cm y CQ = QD. Halla el valor
de PQ.

A 6 cm
B 6,5 cm
C 7 cm
D 8 cm
E 9 cm

A 6 cm
B 7 cm
C 8 cm
D 9 cm
E 5 cm
Los lados diferentes de un romboide se
encuentran en relación de 3 a 4, si el perímetro
es de 84 cm. Calcula la diferencia de las medidas
de estos lados.

A 42 cm
B 21 cm
C 6 cm
D 7 cm
E 12 cm
La suma de las longitudes de las diagonales de un
trapezoide es 30 cm. Encuentra el perímetro del
cuadrilátero que resulta al unir los puntos medios
de los lados del trapezoide.

A 15 cm
B 20 cm
C 30 cm
D 40 cm
E 50 cm
En un cuadrilátero convexo las diagonales son
congruentes. Al unir los puntos medios de los
lados se forma con seguridad:
A Romboide
B Rombo
C Rectángulo
D Trapecio isósceles
E Faltan datos
B
A D
Q
C
P
a
a
θ
θ

96
En un romboide los lados no paralelos miden
3x – 12 y 5x – 8. Determina la medida del lado
menor si su perímetro es 72 cm.

A 20 cm
B 27 cm
C 7 cm
D 9 cm
E 37 cm
Nivel III
19
22
20
23
21 24
Dado el cuadrado ABCD, halla el valor de x.
A 8 cm
B 6 cm
C 12 cm D 6 2 cm
E 12 2 cm
Encuentra el valor de BD, si ABCD es un
paralelogramo.

A 24 cm
B 26 cm
C 28 cm
D 10 cm
E 22 cm
B
A
C
D
9 cm
x
2
3x +
2
cm
O
B C
x
A D
6
cm
Si ABCD es un cuadrado que tiene un perímetro
de 48 cm. Calcula el valor de AE.
Se tiene un cuadrado ABCD cuyo perímetro es
16 mm. Sobre el lado AD se ubica el punto E, tal
que m BCE= 53°. Determina el valor de AE.

A 1 mm
B 2 mm
C 3 mm
D 4 mm
E 5 mm

A 1 cm
B 2 cm
C 3 cm
D 4 cm
E 5 cm
53°
B
A E D
C
En un cuadradoABCD, interiormente se construye
el triángulo equilátero ABR. Encuentra el valor de
la m CRD.

A 80°
B 75°
C 15°
D 150°
E 105°

Test n.° 3
97
En el trapecio isósceles ABCD, AB = 4 2 m.
Calcula la longitud del segmento que une los
puntos medios de las diagonales.
Los ángulos de un cuadrilátero miden 4x,
6x – 20°, 2x + 20° y 5x + 20°. ¿Cuánto mide el
mayor ángulo?
En un trapecio ABCD (BC // AD), halla la
m BDA, si m ABC = 110° y AB = AD.
Grafica el cuadrilátero no convexo ABCD, tal
que m A = 30°, m B = 60° y m C = 50°.
Encuentra el menor valor del ángulo ADC.
En el trapezoide que se muestra, indica el valor
de x.
1 4
2 5
3 6
4 m
A
1 m
C
4 2 m
B
6 m
D
240°
A
120°
C
100°
B
230°
D
100°
A
140°
C
120°
B
150°
D
45°
A
35°
C
25°
B
55°
D
220°
A
120°
C
140°
B
240°
D
110°
A
70°
C
120°
B
90°
D
45°
B
A D
C
110°
130°
x
B
A D
C
I
x
70°
n
n
q q
a
a
b
b

98
En la figura, ABCD es un cuadrilongo tal que
AM = ME, CP = PD, AD = 10 y CD = 6 cm. Calcula
el valor de MP.
En el rectángulo ABCD, halla el valor de x.
En la figura, ABCD es un cuadrilátero regular y
CDE es equilátero, encuentra la m CBE.
Si ABCD es un cuadrado que tiene un perímetro
de 64 cm. Calcula el valor de AE.
Determina el perímetro de un romboide ABCD
en el cual BC = 3(CD), si la bisectriz interior
del ángulo ABC intersecta en F a AD, tal que
FD = a cm.
En el gráfico, ABCD es un paralelogramo,
tal que CD = 12 cm, AM = ME y BN = ND.
Encuentra el valor de MN.
7 10
8 11
9
12
5 cm
A
6 cm
C
7 cm
B
4 cm
D
45°
A
30°
C
15°
B
37°
D
6 cm
A
3 cm
C
4 cm
B
2 cm
D
6 cm
A
8 cm
C
7 cm
B
9 cm
D
8a cm
A
4a cm
C
12a cm
B
16a cm
D
6 cm
A
5 cm
C
3 cm
B
12 cm
D
45°
B
E
M P
A D
C
B
A
x2 + 2x – 2 cm x + 7 + x2 cm
D
C
B
E
A D
C B
A D
E
C
37°
B
A D
q
q
E
C
M N

Tema
99
7
Circunferencia I
Es la figura geométrica que está formada por todos los puntos de un mismo plano que
se encuentran a una misma distancia de otro punto (de ese mismo plano) denominado
centro.
A la distancia constante de estos puntos al centro se le denomina radio de la
circunferencia.
Asimismo, se denomina círculo a la región interior del plano limitada por una circunferencia.
Elementos
- Centro (O): Punto equidistante de todos los puntos que forman la circunferencia. Dos
o más circunferencias con el mismo centro, se dice que son concéntricas.
- Radio (OA): Segmento que une el centro de la circunferencia con un punto cualquiera
de la misma.
- Cuerda (BC): Segmento que une dos puntos de una misma circunferencia.
- Diámetro (DE): Es la cuerda de mayor longitud que pasa por el centro de la
circunferencia dividiéndola en partes congruentes.
- Secante (FG ): Es toda recta ubicada en el plano de la circunferencia que corta a esta
en dos puntos. Cabe notar que la secante contiene a la cuerda.
- Tangente (HI): Es toda recta en el plano de la circunferencia que tiene solo un punto
común llamado punto de tangencia (T).
- Flecha (MN): Segmento levantado perpendicularmente del punto medio de una cuerda
al arco. La prolongación de la flecha siempre pasa por el centro.
- Arco (AN): Es la porción de circunferencia limitada por los extremos de una cuerda.
En particular, una semicircunferencia es un arco limitado por los extremos de un
diámetro.
D E
C
N
B
A
F
R M
O
H
T
I
G
Secante Tangente
La palabra radio
viene del latín radius
que significa «rayo de
luz».
Así llamaban los
romanos a las varitas
que iban del eje a la
llanta de la rueda.
Importante
Circunferencia
Círculo
La circunferencia
tiene longitud:
Lo = 2 r
El círculo tiene área:
S = r2
¿Sabías que...?

100
a = b
Propiedades
1.a Propiedad.- Toda recta tangente a una circunferencia es perpendicular al radio
trazado por el punto de contacto (también llamado punto de tangencia).
2.a Propiedad.- Si el radio es perpendicular a una cuerda. Se convierte en una proporción
de la mediatriz de ella. Además, divide a los arcos que subtiende en dos
partes congruentes.
3.a Propiedad.- En toda circunferencia, a arcos congruentes les corresponden cuerdas
congruentes. Además, están a la misma distancia del centro.
4.a Propiedad.- En una misma circunferencia los arcos comprendidos entre rectas
paralelas son congruentes.
Si OM AB
AM = MB
m AE = m EB
a = b
Si AB CD ⇒
m AB = m CD
a = b
Si M // N ⇒
m AC = m BD
Importante
Importante
Recuerda
Las dos
circunferencias
son concéntricas.
MN: flecha o sagita
* ME: flecha
L
B
M
A
L : mediatriz de AB,
si L AB
⇒ AM = MB
N
r
O
A
M
a a
O
α°
A
B
C
D
α°
M
N
D
B
C
A
α α
O: centro
a = b
OT L1
R
O
r
L1 T (Punto de tangencia)
O
O
E
B
M
A

101
a = b
a = b
a = b
a = b
5.a Propiedad.- Dos rectas tangentes a una misma circunferencia y una cuerda que
una los puntos de tangencia, determinan a un mismo lado, ángulos
congruentes.
α° = β°
d > R + r
d = R + r
Posiciones relativas de dos circunferencias
Dos circunferencias situadas en un mismo plano, con centros O y O' y radios R y r
respectivamente, pueden tener las siguientes posiciones relativas:
Exteriores.- Cuando todos los puntos de una son exteriores a la otra. La distancia entre
sus centros es mayor que la suma de las longitudes de los radios.
Tangentes exteriormente.- Cuando tienen un punto común y los demás puntos de una son
exteriores a la otra. En este caso, sus centros están a lados opuestos de la tangente común y
la distancia entre ellos es igual a la suma de las longitudes de los radios.
Secantes.- Cuando tienen dos puntos comunes. La distancia entre sus centros es menor
que la suma de las longitudes de los radios, pero mayor que su diferencia.
R – r < d < R + r
AB : cuerda común
OO' AB
Observación
Recuerda
Prueba
Si prolongamos los
segmentos tangentes
tendrás:
PA = PB
ya que son
tangentes a la misma
circunferencia
⇒ PAB es
isósceles
⇒ α° = β°
Teorema de la
existencia.
O y O' : centros
O y O': centros
O , O': centros
α°
β°
α°
β°
P
A
B
α°
β°
a
b
x
R r
O O'
d
P
E
R
d
r
O
O'
Q
F
A
R
O O'
B
r
d
a – b < x < a + b

102
a = b
a = b
a = b
d: distancia mínima
entre dos
circunferencias.
D: distancia máxima
entre dos
circunferencias.
Observación
Se dice que dos
circunferencias
se llaman
ortogonales, si
sus radios son
perpendiculares.
AB = CD
d = 0
AB = CD
a = b
d < R ‒ r
a = b
d = R ‒ r
Tangentes interiormente.- Cuando tienen un punto común y todos los puntos de una de
ellas son interiores a la otra. Sus centros están al mismo lado de la tangente común y la
distancia entre ellos es igual a la diferencia de las longitudes de los radios.
Interiores.- Cuando todos los puntos de una de ellas son interiores a la otra. La distancia entre
sus centros es menor que la diferencia de las longitudes de los radios.
Concéntricos.- Cuando tienen el mismo centro, esto es, la distancia entre sus centros es
cero.
Por otro lado, para tres circunferencias es importante considerar el caso de
circunferencias tangentes exteriores dos a dos.
Tangentes comunes interiores
O
O'
O''
r
r
r'
r'
r'' r''
A
C
O
B
D
A, B, C, D son
puntos de tangencia
Teoremas con tangentes
d
O y O': centros
T: punto de tangencia
O y O': centros
O y O', O'': centros
O y O': centros
¿Sabías que...?
R
d
O O'
r
T
D
R
d
O O'
r
O'
O
C
B
A
D

103
Recuerda
AB: indica un
segmento como
figura geométrica.
AB: indica la medida
del segmento AB.
A
B
P
O
r
r
α°
α°
Si A, B, C, D
son puntos de tangencia
⇒ AB = CD
Tangentes comunes exteriores
a) Si A, B y C son puntos de tangencia.
b) Si M es punto medio de AB. Si A y B son puntos de tangencia.
Teoremas de las tangentes a una circunferencia
• Teorema.- Los dos segmentos tangentes a una circunferencia trazados desde un
punto exterior a esta son congruentes y determinan ángulos congruentes con el
segmento que une el punto exterior y el centro de la circunferencia.
a = b
PA = PB
a = b
x = 90°
a = b
x = 90°
PO: bisectriz del ángulo APB
A B
AB = 5u... Incorrecto
m AB = 5u... Correcto
AB = 5u... Correcto
OM: bisectriz del
ángulo AOB.
O
A
B
M
¿Sabías que...?
α°
α°
5u
Veamos:
A M B
R
r
x
A
B
D
C
A
C
x
B
• Teorema.- Los segmentos tangentes comunes externos a dos circunferencias son
congruentes.
a = b
AC = BD
O y O': centros
Si A, B, C, D son
puntos de tangencia
B
A
D
C
O'
O
Observa
r
r: inradio o radio de
la circunferencia
inscrita.

104
Polígonos inscritos en la circunferencia
Un polígono está inscrito en una circunferencia, si sus vértices pertenecen a la
circunferencia.
Polígonos circunscritos en la circunferencia
Un polígono está circunscrito a una circunferencia, si todos sus lados son tangentes a una
circunferencia en su interior.
Teorema de Poncelet
En todo triángulo rectángulo la suma de los catetos es igual a la hipotenusa más el
diámetro de la circunferencia inscrita.
a = b
⇒ a + b = c + 2r
Triángulo
circunscrito
Cuadrilátero
circunscrito
M N
A
B
C
D
T
Sean a, b y c las
longitudes de los lados
Jean Victor Poncelet
es uno de los 72
eruditos recordados
en el friso de las
fachadas de la Torre
Eiffel.
¿Sabías que...?
Triángulo
inscrito
Cuadrilátero
inscrito
B
C
A
Q R
P
S
La semicircunferencia
está inscrita en el
triángulo ABC.
¿Sabías que...?
B
A C
A
B C
r
b
a
c
a = b
¿Sabías que...?
Teorema de Pitot
En un cuadrilátero circunscrito, la suma de las longitudes de dos lados opuestos es
constante e igual al semiperímetro.
a + b = x + y = p
x
x
b
a
y
El teorema de Pitot
lleva el nombre de
su enunciador, el
matemático francés
Henri Pitot (1695 -
1771), quien estudió
matemática por
su cuenta. Fue un
ingeniero y físico
francés además de
militar; construyó
acueductos y desecó
pantanos.
(p = semiperímetro
del cuadrilátero)
Observa
R:circunradio o radio
de la circunferencia
circunscrita.
R

105
a = b
a = b
Recuerda:
En la figura S, M y T son puntos de tangencia. Calcula el valor de x.
Si P y T son puntos
de tangencia.
EP = ET
EO: bisectriz del
ángulo PET.
Resolución:
Resolución:
En la figura O es centro. Halla el valor de x, si m TOC = 2 m TCO. T es punto
de tangencia.
Por teorema, OB es bisectriz del
ángulo B y OC es bisectriz del
ángulo C.
Luego notamos que «O» es excentro
del triángulo ABC, por propiedad del
excentro.
∴ x = 90° –
20°
2
= 80°
Por propiedad OT CT; luego por
ángulo externo: m TOC = 2x
Del dato: m TCO = x
⇒ 2x + x = 90°
∴ x = 30°

Rpta. 80°

Rpta. 30°
1
2
T
x
S
M
20°
T
A
C
O
B
x
S
M
20° a
b
b
a
x
T
O
C
x
x
x
2x
R
R
T
O
C
P
O
T
E
a
a
E: excentro
x = 90° –
m°
2
E
m°
x
b
a
a
b
O
T
L1
T: punto de tangencia.
OT L1
O: centro

106
Calcula el perímetro del triángulo sombreado. Si PA = 8 m.
En la figura mostrada, halla el valor de q, si mQE = 80° y O es el centro.
Halla AT, si AB = 7 cm, BC = 8 cm y AC = 9 cm. T, P y Q son puntos de tangencia.
Resolución:
Resolución:
Resolución:
Si A y B son puntos de tangencia.
Por propiedad: AT = TE; ER = RB; PA = PB
⇒ Perímetro = 2(m + a) = 2AP
Perímetro = 16 m
Trazamos OE EC; luego: m BOE = 2q.
OQ AB; por propiedad OB es bisectriz del
arco QE; luego:
2q =
mQE
2
⇒ q = 20°
Como T, Q y P son puntos de tangencia:
AT = AP = x; TB = BQ = 7 – x; CQ = CP = 9 – x
Pero: BC = 8 = BQ + QC
8 = 7 – x + 9 – x
2x = 8 ⇒ x = 4

Rpta. 16 m

Rpta. 20°

Rpta. 4 cm
3
4
5
Recuerda:
Recuerda:
AT = semiperímetro
del ABC.
AT = p – a
B
A
P
T C
B
Q
A
B
E
R
T
A
P
b
a
m
m + a – b
a
b
A
B
Q
D
C
q
O
E
A C
B
P
T
Q
A C
B
P
T
Q
x
x
7 – x 7 – x
9 – x
8 cm
9 – x
A
T
B
C
a

107
Síntesis
Modela y resuelve
Rpta.
Rpta.
Propiedades:
Teoremas
a = b
a = b
AT = p ‒ a a = b
a + b = m + n
a = b
T. de Poncelet T. de Pitot
a = b
r L1 a = b
AB = AC = R
2 Si P es punto de tangencia y O es el centro de la
circunferencia. Calcula el valor de x.
1 Si P es punto de tangencia y O es el centro de la
circunferencia. Calcula el valor de x.
110° x
P
A
O
r
x 30°
P
A
O
r
Circunferencia I
AT = semiperímetro del ABC

108
4 Halla el valor de x, si T y M son puntos de
tangencia.
3 Si A y B son puntos de tangencia, halla el valor de n.
2n2
‒ 52
n
2 ‒ 3
P
A
B
T
M
x ‒ 2
11
A
5 El perímetro de ABC es 40 cm y AB = 10 cm.
Encuentra el valor de MC (M punto de tangencia).
6 En la figura, la circunferencia está inscrita, si
AB = 5 u, BC = 7 u y AC = 8 u. Encuentra el valor
de AD.
B
C
M
A
B
C
D
A
7 En la figura, la circunferencia está inscrita en el
triángulo rectángulo ABC. Si AB = a + 3, BC = a + 6 y
AC = 2a + 3. Determina la medida del radio r.
8 En la figura, la circunferencia está inscrita en un
triángulo rectángulo. Si AB = 9 u. Determina la
medida del radio r.
C
A
B
O
r
C
A
B
O
r
53°
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.

109
10 En la figura, calcula el valor de a + b, si T, R y Q
son puntos de tangencia.
9 En la figura, calcula el valor de x, si P, Q y T son
puntos de tangencia.
5 u
Q
T
x
4 u
P
cuadrilátero. Si AB = 5 u, BC = 4 u AD = 8 u y EC = 7
u. Halla el valor de x.
cuadriláteroABCD. SiAB = 9 u,AD = 10 u y EC = 8 u.
Halla el valor de BC.
C
B
A D
x
70°
E
C
B
A D
β°
E
β°
13 En la figura, AD es diámetro y BC // AD. Encuentra
el valor de x.
14 En la figura, BC // AD. Encuentra el valor de x. Si
además m ABCD= 160°.
A D
O
50°
x
C
B
A D
70°
x
C
B
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
T
Q
R
12 cm
a b
a b

110
17 Si AC – AB = 6 cm y M es punto medio de BC,
calcula el valor de EM (E es punto de tangencia).
18 ElperímetrodeABCes30cm.Calculaelvalorde TC
(T punto de tangencia).
15 En un triángulo rectángulo de semiperímetro igual
a 20 u y de inradio 7 u. Determina la longitud de la
hipotenusa.
16 El perímetro de un triángulo rectángulo es
90 cm y el radio de la circunferencia inscrita 4 cm.
Determina la longitud de la hipotenusa.
Resolución:
Resolución:
Resolución:
Resolución:
C
A
B
E
M
C
A
T
B
19 ABC es equilátero; AD + EC = 6 cm. Halla el
perímetro del triángulo ABC. Si D y E son puntos
de tangencia.
20 Si el perímetro del triángulo regular ABC es 27 u.
Halla AD + CE, si D, E, F son puntos de tangencia.
A C
F
D
E
B
A C
D E
B
F
Rpta.
Rpta.
Rpta.
Rpta.
Rpta. Rpta.

111
Nivel I
1
2
3
6
4
5
En la figura, M, N y P son puntos de tangencia;
si AC = 15 cm. Calcula el valor de AB + BC.
En la figura, R, S, T y P son puntos de tangencia;
si AB = 6 cm, BC = 8 cm y CD = 10 cm. Halla el
valor de AD.
En la figura,L1 // L2, A y B son puntos de tangencia.
Determina m POQ, además O es el centro.
En la figura, R y S son puntos de tangencia.
Encuentra el valor de RS.
En la figura, la circunferencia es tangente a los 3
lados, O es el centro. Si m B = 40°. Calcula el
valor de x.
B
S C
T
D
P
A
R
B
O
A C
x°

A 33 cm
B 30 cm
C 32 cm
D 34 cm
E 31 cm

A 4 cm
B 3 cm
C 2 cm
D 1 cm
E 5 cm

A 100°
B 110°
C 120°
D 130°
E 140°

A 6 cm
B 9 cm
C 7 cm
D 8 cm
E 10 cm
L1
P
Q
O
L2
A
B
P
R
6 cm
O
S 2 cm
M
N
P
C
A
8 cm
O
B

A 70o
B 80o
C 90o
D 100o
E 120o
Si O es el centro, T es punto de tangencia y
la m OAT = 20°. Halla la m PTA.
A
O
P T

A 50°
B 90°
C 80°
D 70°
E 60°

112
En la figura, A y B son puntos de tangencia.
Determina el valor de 2x.
x
A
B
20º

A 150°
B 170°
C 160°
D 180°
E 190°
En la figura, T, P y Q son puntos de tangencia.
Encuentra: m TOP + m BOC.
Nota: B, O y P no son colineales.

A 230°
B 240°
C 220°
D 260°
E 250°
40°
T
B
Q
O
C
P
A
En la figura, M, N, P y Q son puntos de tangencia,
si AB + CD = 20 cm, AD = 12 cm. Calcula el valor
de MC.

A 2 cm
B 6 cm
C 5 cm
D 3 cm
E 4 cm
M
B
N
A
P
D
Q
C
7 10
8 11
9 12
En un triángulo ABC: AB = 8 cm, BC = 10 cm
y AC = 12 cm. Si la circunferencia inscrita
determina sobre AC el punto M. Halla el valor de
AM.

A 3 cm
B 4 cm
C 5 cm
D 6 cm
E 2 cm
Determina el valor de x, si A y B son puntos de
tangencia. O es el centro.
40°
A B
C
O
x

A 70o
B 50o
C 40o
D 60o
E 30o
En la figura, R, T y S son puntos de
tangencia; si AB = 13 cm, BC = 14 cm y AC = 15
cm. Encuentra el valor de AS.
A S C
T
R
B

A 10 cm
B 6 cm
C 7 cm
D 9 cm
E 8 cm

113
16
10
17
14
13
18
15
En la figura mostrada, m AB = 80° y m BC = 60°.
Halla el valor de (x – y).
C
B
A
D
O
P
x
y

A 13°
B 10°
C 12°
D 14°
E 11°
Determina el valor de AB. Si se sabe que EB = 3 m
y BF = 1 m.
E B F
R
A

A 6 m
B 5 m
C 4 m
D 2 m
E 3 m
En la figura mostrada, calcula el valor de x
si m TNB = 48° y NT // AM.

A 3°
B 5°
C 10°
D 4°
E 6°
M
B
A
x r
N
T
Nivel II
Calcula la longitud del segmento LM. Si se sabe
que NB = 4 u; O1 y O2 son centros.
O1
B
N
M
L
A
O2

A 3 u
B 2 u
C 2,5 u
D 4 u
E 4,5 u
En la figura, M, N y P son puntos de tangencia; si
AC = 15 cm. Encuentra el valor de AB + BC.

A 23 cm
B 20 cm
C 22 cm
D 24 cm
E 21 cm
M
B
N
P
C
A
O 3 cm
Las longitudes de las circunferencias concéntricas
son 31,40 cm y 18,84 cm. Halla el valor de
AB (π = 3,14), si O es el centro.

A 2 cm
B 3 cm
C 3,2 cm
D 4 cm
E 4,5 cm
A
B
O

114
En la figura, determina la medida del ángulo COD,
si se muestra un trapecio en la figura.
B
A
C
D
O

A 60°
B 90°
C 80°
D 100°
E Faltan datos
Si P, Q y R son puntos de tangencia y m ABP = 36°,
encuentra el valor de x.

A 36°
B 30 °
C 32°
D 34°
E 31°
En el gráfico mostrado, calcula el valor de α. Si O
es el centro.

A 115°
B 135°
C 150°
D 120°
E 160°
α
O
B
x
α
α
Q
C
P
A R
36°
Nivel III
19
20
21
Si A, B y P son puntos de tangencia, además
AP = MP. Halla el valor de α.
B
M
N
A
P
α°

A 45°
B 30°
C 60°
D 37°
E Faltan datos
En la figura, O es el centro y AO = EC, indica la
relación correcta entre α° y θ°.
En la figura, determina el valor de x si P y S son
centros. También Q y R son puntos de tangencia.
P S
Q
R
40° x

A 90°
B 40°
C 80°
D 50°
E 70°
α
θ
D
A O C
E
A
1
2
B
3
4

C
1
3
D
2
3

E 1
4
22
23
24

Tema
115
8
Circunferencia II
Observa
Ángulo central: Es el ángulo que tiene su vértice en el centro de la circunferencia y sus
lados son los radios.
El ángulo y el arco subtendido son iguales en medida.
Para dividir la circunferencia del reloj en 12 partes exactamente iguales, que a futuro
podrán dar una medición perfecta de la hora, es necesario usar criterios de ángulos de
la circunferencia.
Ángulo semiinscrito: Es aquel ángulo cuyo vértice está sobre la circunferencia y es
formado por una tangente y una cuerda.
Ángulo inscrito: Es aquel ángulo formado por dos cuerdas que concurren en un punto
de la circunferencia. Este ángulo mide la mitad del arco subtendido.
Siendo AB diámetro
y P un punto
cualquiera de la
circunferencia,
entonces el ángulo
de vértice P en el
triángulo APB es
recto.
Ángulos en la circunferencia
a = b
x = θ°
a = b
x = θ°
2
a = b
x = m BC
2
B
O
A
AB: es el arco
subtendido por el
ángulo AOB.
A
B
x
C
θ° x = 90°
x = a + b
m APB = 90°
A
B
O x
R
R
θ°
C
B
x
T
θ°
A B
P
x

116
Recuerda
Ángulo exterior: Es aquel ángulo cuyo vértice está en el exterior de la circunferencia. Su
medida es la semidiferencia de los arcos que abarcan sus lados sobre la circunferencia.
Hay tres casos y son:
¡Ahora a experimentar!
Caso 1: Con dos rectas tangentes.
Caso 2: Con una recta tangente y una recta secante.
Caso 3: Con dos rectas secantes.
a = b
x =
a° ‒ θ°
2
a = b
x =
a° ‒ θ°
2
a = b
x =
a° ‒ θ°
2
T
L1
L1: recta tangente
T: punto de tangencia
L2: recta secante
A, B: puntos de corte
L3: recta pasante o
recta exterior
A B
L2
L3
Ángulo interior: Es aquel ángulo cuyo vértice está en el interior de la circunferencia y está
formado por dos cuerdas secantes. Su medida es la semisuma de la medida de los arcos
comprendidos.
a = b
x =
α° + θ°
2
A y C son puntos
de tangencia
A es punto de
tangencia
B
A
D
C
α°
F
x
θ°
A
B
θ°
x
C
D
α°
D
A
θ°
B
C
α°
F
x
A
B
θ°
x
C
α°
Ángulo ex-inscrito: Es aquel ángulo formado por una secante y una cuerda concurrentes
en un punto de la circunferencia.
a = b
x = m AC
2
A
B
x
C
Q

117
Recuerda
Calcula la medida del ángulo TOA, si AT es una recta tangente y O es el centro.
Resolución:
∴ m TOA = 70°
Halla el valor de x si BC // AD.
A D
30°
x
B C
A D
30°
60° x
B C
100°
x
A
C
B
α°
A
C
B
Por la propiedad de las cuerdas paralelas:
x = 60°
Resolución:
«B» por ser ángulo inscrito se cumple:
x =
100°
2
⇒ x = 50°
Resolución:
Si L // L1:
⇒ α° = β°
m AC = 2α
a° + β°
2
x =
m AB = 2β
A
B
β°
x
β° α°
L
L1
α° β°
20°
T
A
O
20°
70°
T
A
O
Por teorema, el radio con la tangente
forman un ángulo de 90°.

Rpta. 70°

Rpta. 60°

Rpta. 50°
Por el ángulo inscrito se cumple que
m AB = 60°.
1
2
3

118
Recuerda
No olvides
Nota
Resolución:
Por ser ángulo interior se cumple:
x = 140°
2
x = 80° + 60°
2
⇒ x = 70°
Resolución:
Por ser ángulo exterior se cumple:
x = 50°
2
x =
90° ‒ 40°
2
⇒ x = 25°
α° ‒ β°
2
x =
Determina el valor de m BC.
Resolución:
Por ser ángulo semiinscrito se cumple:
BC
2
= 60°
BC = 120°
α°
β° x
¿Cuál es el arco AB?
¿El rojo o el azul?
Rpta. El arco AB es
el rojo, ya que el
azul es el arco AQB.
AQB se lee: arco AQB.
B
A 60°
D
C
80°
F
x
D
A
40°
B
C
90°
F
x

Rpta. 70°

Rpta. 120°

Rpta. 25°
A
B
Q
4
5
6
60°
B
C

119
Recuerda
En la figura, encuentra el valor de x si PQ = QT.
En la figura, determina el valor de x si m ABC = 120°.
Resolución:
Resolución:
Por ángulo inscrito:
m MNP = 35°
luego, PQ = QT
⇒ MPTN es un trapecio:
x
2
= 35°
x = 70°
Por ángulo inscrito:
mED = 80°
Luego, notemos que «x» es un ángulo
interior que cumple:
x =
120° + 80°
2
x = 100°

Rpta. 70°

Rpta. 100°
7
8
mTB = 2m TAB
70°
x
P
T
M
N
Q
70°
x
P
T
M
N
Q
35°
x
2
A
E
D
B
C
x
40°
A
E
D
B
C
x
40°
80°
120°
α + β
2
x =
2a
A
T
B
a
b° x a°

120
x
Síntesis
a = b
O: centro
a = b
x = 45°
a = b
x =
α° + β°
2 a = b
m AB = 2α°
a = b
m AB = 2β°
a = b
α° + β° = 180°
a = b
Si AB: diámetro
x = 90º
2α°
α°
α° α°
O
x α°
β°
B
A
α°
B
P
A
β°
A B
x
a = b
x =
α ° ‒ θ°
2
a = b
x = θ°
2
A
B
θ°
x
C
α°
A
B
θ°
x
C
D
α°
D
A
θ°
B
C
α°
F
x
A
B
C
α° β°
θ°
x
Circunferencia II

121
Modela y resuelve
4 Si m AC = 84° y B es un punto que pertenece a la
circunferencia. Halla el valor de x.
3 Si B es un punto que pertenece a la circunferencia.
5 Si A es punto de tangencia. Determina el valor de x.
2 Calcula el valor de x, si O es el centro de la
circunferencia.
6 Determina el valor de x, si m ABC = 260° y A es
punto de tangencia.
1 Calcula el valor de x, si O es el centro de la
circunferencia.
60°
x
O
48° x
B
C
A
x B
C
A
6x
60°
O
94°
x
B
A
C
x
B
A
Resolución:
Resolución:
Resolución:
Resolución:
Resolución:
Resolución:
7 Encuentra el valor de x. 8 Encuentra AE, si m BD = 50°.
40°
B
D
C
A
E
30°
x
110°
B
D
C
A
F
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.

122
9 Calcula el valor de x, si m PQR = 280°. 10 Calcula el valor de x.
R
P
Q
x
x 100°
B
T
A
11 En la circunferencia, AB es diámetro; halla el valor
de x.
12 En la circunferencia, AB es diámetro; halla el valor
de x.
40°
B
A
C
D
O P
E x
Resolución:
Resolución:
Resolución:
Resolución:
120°
B
A
C
D
O
E x
13 En la figura, A y B son puntos de tangencia;
determina el valor de x.
14 En la figura, T es punto de tangencia y
m ATP = 40º. Determina el valor de x.
36°
A
P
B
E
x
35°
A
T
P
B
x
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.
Rpta.

123
Nivel I
1
2
5
3
6
4
Calcula el valor de x, si AB = CF.
A 20°
B 30°
C 32°
D 34°
E 31°
Determina el valor de x, sabiendo que RS, TS, QS
y PS son líneas tangentes.
A 80°
B 60°
C 70°
D 75°
E 65°
R
A
Q
C P
T
B
β
S
x
α 40°
Calcula el valor de x, si AB = BC = CD.
A 33°
B 30°
C 32°
D 34°
E 31°
x
40°
A
B
C
D
Si m AB = m DE y m BC = m CD.
A 33°
B 30°
C 35°
D 34°
E 31°
Halla la medida del arco MPN, si MN y el radio
tienen medidas iguales.
A 280°
B 230°
C 225°
D 270°
E 300°
Halla el valor de x, si m APB = 2x y m AB = x.
A 72°
B 144°
C 126°
D 200°
E 120°
70°
x
F
A
B
C
D
E
2x x
A
B
P
O
M
N
P
R
70°
x
A
B
F
C
D E

Geometría 2 delta

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Similar a Geometría 2 delta

Similar a Geometría 2 delta (20)

Último

Último (20)

Geometría 2 delta